Файл: Исследовательская работа Производная в жизни человека Авторы Андреева Н. В. с. Красноармейское 2015 Содержание I. Введение. Ii. История производной.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 236
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
помощью ее производной примерно по схеме
При исследовании свойств функции полезно найти:
Результаты исследования удобно записать в виде таблицы.
Затем, используя таблицу, строим график функции. Для более точного построения графика обычно находят точки его пересечения с осями координат и, если необходимо, еще несколько точек графика.
Используя результаты исследования, построим график функции:
y= 3x5- 5x3 + 2
Решение: 1) Область определения – вся числовая ось R.
при х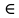 [- 1; 1 ] – функция убывает.
[- 1; 1 ] – функция убывает.
В точке х = 1 – минимум, причем ymin = 0.
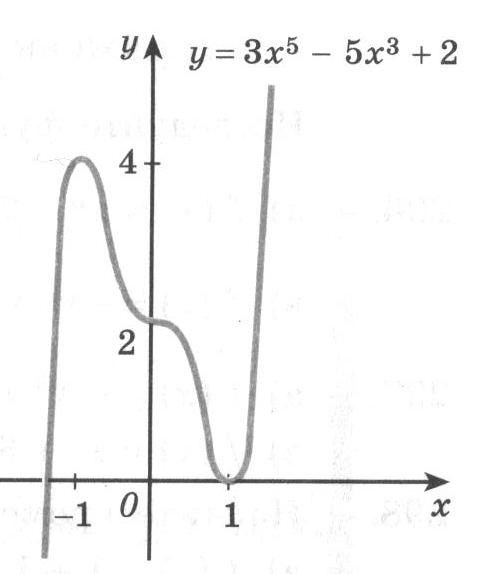
рис.3
II. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
Производная широко используются в различных областях деятельности человека, поэтому умение прогнозировать, решать имеет огромную роль в практической деятельности. Производная относится к числу математических понятий, которые носят межпредметный характер, и широко применяются в физике, химии, биологии, в технике и других отраслях наук. Изучение материала по этой теме имеет принципиально важное значение, так как здесь показывается приложение к решению различных физических и технических задач, то есть возможности применения элементов дифференциального исчисления в описании и изучении процессов и явлений реального мира.
Еще Гете сказал: "Просто знать - ещё не всё, знания нужно использовать".
1. Производная в физике
1)Скорость и ускорение
Понятие производной возникло как математическое описание скорости движения. Поэтому важнейшим приложением производной является вычисление скорости. Скорость произвольно движущейся точки является векторной величиной, так как она определяется с помощью вектора — перемещения точки за промежуток времени. Рассмотрим сначала простейший случай: движение точки по прямой. При прямолинейном движении точки ее положение, перемещение, скорость, ускорение и другие характеристики, которые имеют векторный смысл, можно задать одним числом, т. е, считать скалярными величинами.
Ускорение произвольного движения определяется как скорость изменения скорости, т. е. как производная скорости по времени: а = v΄. Так как скорость производная координаты, а ускорение есть производная скорости, то ускорение называют второй производной координаты и обозначают: а = х΄΄.
Через координату точки х = х(t) и ее производные можно выразить другие механические величины:
cила F = ma = mx΄΄, где m – масса,
импульс P = mv = mx΄,
кинетическая энергия E =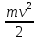 =
=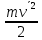
Основой разнообразных физических приложений производной является понятие дифференциала.
Дифференциалом функции называют произведение ее производной на приращение аргумента.
dy = f΄(x)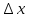 или f΄(x) =
или f΄(x) = 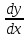
Для вычисления дифференциала в физике достаточно знать , что дифференциал – это главная часть приращения функции, линейно зависящая от приращения аргумента. Тогда, в равенстве
dy = kdx имеется ввиду, что k – это производная y по х.
2)Работа.
Рассмотрим работу, которую совершает заданная сила F при перемещении по отрезку оси х. Если сила F постоянна, то работа А равна произведению F на длину пути. Если сила меняется, то ее можно рассматривать как функцию от х, т. е.
F = F(x). Приращение работы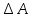 на отрезке [x; x +
на отрезке [x; x +  ] нельзя точно вычислить как произведение F(x)dx, так как сила меняется на этом отрезке. Однако при маленьких dx можно считать, что сила меняется незначительно и произведение представляет собой главную часть
] нельзя точно вычислить как произведение F(x)dx, так как сила меняется на этом отрезке. Однако при маленьких dx можно считать, что сила меняется незначительно и произведение представляет собой главную часть 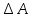 , т. е. является дифференциалом работы: dA = F(x)dx.
, т. е. является дифференциалом работы: dA = F(x)dx.
Таким образом, силу можно считать производной работы по перемещению.
3) Заряд.
Пусть q – заряд, переносимый электрическим током через поперечное сечение проводника за время t. Если сила тока I постоянна, то за время dt ток перенесет заряд, равный Idt.
При силе тока, изменяющейся со временем по некоторому закону I = I(t) произведение I(t)dt дает главную часть приращения заряда на маленьком отрезке времени [t; t +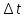 ], т. е. является дифференциалом заряда: dq = I(t)dt. Снова получаем, что сила тока является производной заряда по времени.
], т. е. является дифференциалом заряда: dq = I(t)dt. Снова получаем, что сила тока является производной заряда по времени.
4)Масса тонкого стержня.
Пусть есть неоднородный тонкий стержень. Если ввести координаты так, как показано на рисунке 4., то можно рассмотреть функцию m = m(l) – массу куска стержня от точки О до точки l.
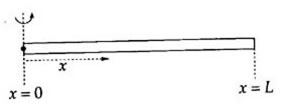
Неоднородность стержня означает, что его линейная плотность не является постоянной, а зависит от положения точки l по некоторому закону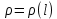 . Если на маленьком отрезке стержня [l; l + dl] мы будем считать плотность постоянной и равной
. Если на маленьком отрезке стержня [l; l + dl] мы будем считать плотность постоянной и равной 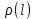 , то произведение
, то произведение 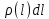 дает нам дифференциал массы – dm. Это значит, что линейная плотность – это производная массы по длине.
дает нам дифференциал массы – dm. Это значит, что линейная плотность – это производная массы по длине.
5)Теплота.
Рассмотрим процесс нагревания какого-либо вещества и будем вычислять количество теплоты Q(T), которое необходимо, чтобы нагреть 1 кг этого вещества от 0° до T° (по Цельсию). Зависимость Q = Q(T) очень сложна и определяется из опыта. Если бы удельная теплоемкость с данного вещества не зависела от температуры , то произведение cdT дало бы нам изменение количества теплоты. Считая на малом отрезке [T; T + dT] удельную теплоемкость постоянной, мы получим дифференциал теплоты dQ как c(T)dT. Поэтому теплоемкость – это производная теплоты по температуре.
6)Работа как функция времени.
Нам известна характеристика работы, определяющая ее скорость по времени, - это мощность. При работе с постоянной мощностью N работа за время dt равна Ndt. Это выражение представляет собой дифференциал работы, т. е. dA = N(t)dt и мощность выступает как производная работы по времени.
в) Задачи на применение производной в физике
В физике производная применяется в основном для вычисления наибольших или
наименьших значений для каких-либо величин.
Задача 1.
Лестница длиной 5м приставлена к стене таким образом, что верхний ее конец
находится на высоте 4м. В некоторый момент времени лестница начинает
падать, при этом верхний конец приближается к поверхности земли с
постоянным ускорением 2 м/с2. С какой скоростью удаляется от стены
нижний конец лестницы в тот момент, когда верхний конец находится на высоте
2м?
Задача 2. Дождевая капля падает под действием силы тяжести; равномерно испаряясь так,
что ее масса m изменяется по закону m(t) = 1 - 2/3t. (m изменяется в
граммах, t - в секундах). Через сколько времени после начала падения
кинематическая энергия капли будет наибольшей?
Задача 3. Источник тока с электродвижущей силой Е=220 В и внутренним сопротивлением
r = 50 Ом подключен к прибору с сопротивлением R.Чему должно быть равно
сопротивление R потребителя, чтобы потребляемая им мощность была
наибольшей?
Двадцатый век называют по-разному. И ядерным веком, и ракетным, и космическим. Но самым точным было и остается название: век электричества. Доказывать это не нужно. Достаточно посмотреть вокруг. В наших домах, на транспорте, на заводах : всюду работает электрический ток. В цепи электрического тока электрический заряд меняется
с течением времени по закону q=q (t).
Сила тока I есть производная заряда q по времени I = q΄(t).
З а д а ч а 1.
Заряд, протекающий через проводник , меняется по закону q = sin(2t - 10).
Найти силу тока в момент времени t=5 cек.
Решение:
I = (q(t))΄= 2cos(2t - 10), I(5) = 2 cos(2·5 - 10)= 2cos0 = 2(A)
Ответ: 2А
З а д а ч а 2.
Электронагревательный прибор потребляет мощность от источника тока, ЭДС которого равна 3В, а внутреннее сопротивление равно 2Ом. Какое сопротивление должен иметь прибор, чтобы в нем выделялась максимальная мощность?
Решение:
Мощность, потребляемая электронагревательным прибором, сопротивление которого равно R, находится по формуле P =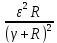 . Обозначим сопротивление прибора R = х. С учетом данных задачи составим функцию y = P(x) =
. Обозначим сопротивление прибора R = х. С учетом данных задачи составим функцию y = P(x) = 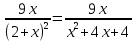 .
.
Область определения этой функции промежуток (0; +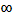 ). Исследуем полученную функцию на экстремум.
). Исследуем полученную функцию на экстремум.
y΄ = P΄(x) = (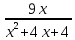 )΄ =
)΄ = 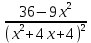
Критические точки найдутся из уравнения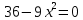 . х1 = – 2 точка не входит в область определения функции, тогда х2 = 2. Найдем знак производной на каждом промежутке: (0; 2) y΄ > 0, (2; +
. х1 = – 2 точка не входит в область определения функции, тогда х2 = 2. Найдем знак производной на каждом промежутке: (0; 2) y΄ > 0, (2; + ) y΄ < 0
) y΄ < 0
Так как при переходе через точку х = 2 производная меняет знак с плюса на минус, то в этой точке функция имеет максимум. Значит, мощность, потребляемая прибором, будет наибольшей, если сопротивление его равно 2 Ом.
Большую часть своих усилий человек тратит на поиск наилучшего, оптимального решения поставленной задачи. Как, располагая определенными ресурсами, добиться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени – так ставят вопросы, над которыми приходится думать каждому члену общества. Не все такие задачи поддаются точному математическому описанию, не для всех из них найдены короткие пути решения. Однако часть таких задач поддается исследованию с помощью методов математического анализа – это задачи, которые можно свести к нахождению наибольшего или наименьшего значения функции.
Наиболее важной для приложений ситуацией является следующая: функция f задана на отрезке [a;b] и имеет производную во всех точках этого отрезка. Тогда для нахождения наибольшего и наименьшего значений этой функции надо поступить так:
Найти критические точки (в данном случае корни производной), вычислить значения функции во всех критических точках и на концах отрезка, из найденных значений найти наибольшее и наименьшее.
При исследовании свойств функции полезно найти:
-
область ее определения; -
производную; -
стационарные точки; -
промежутки возрастания и убывания; -
точки экстремума и значения функции в этих точках.
Результаты исследования удобно записать в виде таблицы.
Затем, используя таблицу, строим график функции. Для более точного построения графика обычно находят точки его пересечения с осями координат и, если необходимо, еще несколько точек графика.
Используя результаты исследования, построим график функции:
y= 3x5- 5x3 + 2
Решение: 1) Область определения – вся числовая ось R.
-
Производная функции равна: y ΄ = 15x4 – 15x2. -
Находим критические точки: при y ΄ = 0, x = 0, х = 1 и х = - 1 -
исследуем промежутки: при х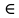 (-
(- 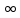 ; - 1]
; - 1] 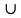 [1; +
[1; + 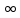 ) – функция возрастает,
) – функция возрастает,
при х
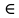 [- 1; 1 ] – функция убывает.
[- 1; 1 ] – функция убывает.-
В точке х = - 1 – максимум, причем ymax = 4.
В точке х = 1 – минимум, причем ymin = 0.
-
y = 0 при х = 0, х = 0 – не является точкой экстремума. -
Строим график функции:

рис.3
II. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
Производная широко используются в различных областях деятельности человека, поэтому умение прогнозировать, решать имеет огромную роль в практической деятельности. Производная относится к числу математических понятий, которые носят межпредметный характер, и широко применяются в физике, химии, биологии, в технике и других отраслях наук. Изучение материала по этой теме имеет принципиально важное значение, так как здесь показывается приложение к решению различных физических и технических задач, то есть возможности применения элементов дифференциального исчисления в описании и изучении процессов и явлений реального мира.
Еще Гете сказал: "Просто знать - ещё не всё, знания нужно использовать".
1. Производная в физике
1)Скорость и ускорение
Понятие производной возникло как математическое описание скорости движения. Поэтому важнейшим приложением производной является вычисление скорости. Скорость произвольно движущейся точки является векторной величиной, так как она определяется с помощью вектора — перемещения точки за промежуток времени. Рассмотрим сначала простейший случай: движение точки по прямой. При прямолинейном движении точки ее положение, перемещение, скорость, ускорение и другие характеристики, которые имеют векторный смысл, можно задать одним числом, т. е, считать скалярными величинами.
Ускорение произвольного движения определяется как скорость изменения скорости, т. е. как производная скорости по времени: а = v΄. Так как скорость производная координаты, а ускорение есть производная скорости, то ускорение называют второй производной координаты и обозначают: а = х΄΄.
Через координату точки х = х(t) и ее производные можно выразить другие механические величины:
cила F = ma = mx΄΄, где m – масса,
импульс P = mv = mx΄,
кинетическая энергия E =
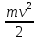 =
=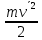
Основой разнообразных физических приложений производной является понятие дифференциала.
Дифференциалом функции называют произведение ее производной на приращение аргумента.
dy = f΄(x)
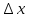 или f΄(x) =
или f΄(x) = 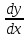
Для вычисления дифференциала в физике достаточно знать , что дифференциал – это главная часть приращения функции, линейно зависящая от приращения аргумента. Тогда, в равенстве
dy = kdx имеется ввиду, что k – это производная y по х.
2)Работа.
Рассмотрим работу, которую совершает заданная сила F при перемещении по отрезку оси х. Если сила F постоянна, то работа А равна произведению F на длину пути. Если сила меняется, то ее можно рассматривать как функцию от х, т. е.
F = F(x). Приращение работы
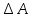 на отрезке [x; x +
на отрезке [x; x +  ] нельзя точно вычислить как произведение F(x)dx, так как сила меняется на этом отрезке. Однако при маленьких dx можно считать, что сила меняется незначительно и произведение представляет собой главную часть
] нельзя точно вычислить как произведение F(x)dx, так как сила меняется на этом отрезке. Однако при маленьких dx можно считать, что сила меняется незначительно и произведение представляет собой главную часть 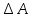 , т. е. является дифференциалом работы: dA = F(x)dx.
, т. е. является дифференциалом работы: dA = F(x)dx. Таким образом, силу можно считать производной работы по перемещению.
3) Заряд.
Пусть q – заряд, переносимый электрическим током через поперечное сечение проводника за время t. Если сила тока I постоянна, то за время dt ток перенесет заряд, равный Idt.
При силе тока, изменяющейся со временем по некоторому закону I = I(t) произведение I(t)dt дает главную часть приращения заряда на маленьком отрезке времени [t; t +
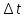 ], т. е. является дифференциалом заряда: dq = I(t)dt. Снова получаем, что сила тока является производной заряда по времени.
], т. е. является дифференциалом заряда: dq = I(t)dt. Снова получаем, что сила тока является производной заряда по времени.4)Масса тонкого стержня.
Пусть есть неоднородный тонкий стержень. Если ввести координаты так, как показано на рисунке 4., то можно рассмотреть функцию m = m(l) – массу куска стержня от точки О до точки l.

Неоднородность стержня означает, что его линейная плотность не является постоянной, а зависит от положения точки l по некоторому закону
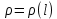 . Если на маленьком отрезке стержня [l; l + dl] мы будем считать плотность постоянной и равной
. Если на маленьком отрезке стержня [l; l + dl] мы будем считать плотность постоянной и равной 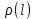 , то произведение
, то произведение 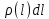 дает нам дифференциал массы – dm. Это значит, что линейная плотность – это производная массы по длине.
дает нам дифференциал массы – dm. Это значит, что линейная плотность – это производная массы по длине.5)Теплота.
Рассмотрим процесс нагревания какого-либо вещества и будем вычислять количество теплоты Q(T), которое необходимо, чтобы нагреть 1 кг этого вещества от 0° до T° (по Цельсию). Зависимость Q = Q(T) очень сложна и определяется из опыта. Если бы удельная теплоемкость с данного вещества не зависела от температуры , то произведение cdT дало бы нам изменение количества теплоты. Считая на малом отрезке [T; T + dT] удельную теплоемкость постоянной, мы получим дифференциал теплоты dQ как c(T)dT. Поэтому теплоемкость – это производная теплоты по температуре.
6)Работа как функция времени.
Нам известна характеристика работы, определяющая ее скорость по времени, - это мощность. При работе с постоянной мощностью N работа за время dt равна Ndt. Это выражение представляет собой дифференциал работы, т. е. dA = N(t)dt и мощность выступает как производная работы по времени.
в) Задачи на применение производной в физике
В физике производная применяется в основном для вычисления наибольших или
наименьших значений для каких-либо величин.
Задача 1.
Лестница длиной 5м приставлена к стене таким образом, что верхний ее конец
находится на высоте 4м. В некоторый момент времени лестница начинает
падать, при этом верхний конец приближается к поверхности земли с
постоянным ускорением 2 м/с2. С какой скоростью удаляется от стены
нижний конец лестницы в тот момент, когда верхний конец находится на высоте
2м?
Задача 2. Дождевая капля падает под действием силы тяжести; равномерно испаряясь так,
что ее масса m изменяется по закону m(t) = 1 - 2/3t. (m изменяется в
граммах, t - в секундах). Через сколько времени после начала падения
кинематическая энергия капли будет наибольшей?
Задача 3. Источник тока с электродвижущей силой Е=220 В и внутренним сопротивлением
r = 50 Ом подключен к прибору с сопротивлением R.Чему должно быть равно
сопротивление R потребителя, чтобы потребляемая им мощность была
наибольшей?
-
Производная в электротехнике
Двадцатый век называют по-разному. И ядерным веком, и ракетным, и космическим. Но самым точным было и остается название: век электричества. Доказывать это не нужно. Достаточно посмотреть вокруг. В наших домах, на транспорте, на заводах : всюду работает электрический ток. В цепи электрического тока электрический заряд меняется
с течением времени по закону q=q (t).
Сила тока I есть производная заряда q по времени I = q΄(t).
З а д а ч а 1.
Заряд, протекающий через проводник , меняется по закону q = sin(2t - 10).
Найти силу тока в момент времени t=5 cек.
Решение:
I = (q(t))΄= 2cos(2t - 10), I(5) = 2 cos(2·5 - 10)= 2cos0 = 2(A)
Ответ: 2А
З а д а ч а 2.
Электронагревательный прибор потребляет мощность от источника тока, ЭДС которого равна 3В, а внутреннее сопротивление равно 2Ом. Какое сопротивление должен иметь прибор, чтобы в нем выделялась максимальная мощность?
Решение:
Мощность, потребляемая электронагревательным прибором, сопротивление которого равно R, находится по формуле P =
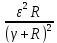 . Обозначим сопротивление прибора R = х. С учетом данных задачи составим функцию y = P(x) =
. Обозначим сопротивление прибора R = х. С учетом данных задачи составим функцию y = P(x) = 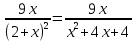 .
. Область определения этой функции промежуток (0; +
y΄ = P΄(x) = (
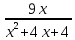 )΄ =
)΄ = 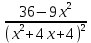
Критические точки найдутся из уравнения
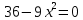 . х1 = – 2 точка не входит в область определения функции, тогда х2 = 2. Найдем знак производной на каждом промежутке: (0; 2) y΄ > 0, (2; +
. х1 = – 2 точка не входит в область определения функции, тогда х2 = 2. Найдем знак производной на каждом промежутке: (0; 2) y΄ > 0, (2; + ) y΄ < 0
) y΄ < 0Так как при переходе через точку х = 2 производная меняет знак с плюса на минус, то в этой точке функция имеет максимум. Значит, мощность, потребляемая прибором, будет наибольшей, если сопротивление его равно 2 Ом.
-
Задачи на максимум и минимум
Большую часть своих усилий человек тратит на поиск наилучшего, оптимального решения поставленной задачи. Как, располагая определенными ресурсами, добиться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени – так ставят вопросы, над которыми приходится думать каждому члену общества. Не все такие задачи поддаются точному математическому описанию, не для всех из них найдены короткие пути решения. Однако часть таких задач поддается исследованию с помощью методов математического анализа – это задачи, которые можно свести к нахождению наибольшего или наименьшего значения функции.
Наиболее важной для приложений ситуацией является следующая: функция f задана на отрезке [a;b] и имеет производную во всех точках этого отрезка. Тогда для нахождения наибольшего и наименьшего значений этой функции надо поступить так:
Найти критические точки (в данном случае корни производной), вычислить значения функции во всех критических точках и на концах отрезка, из найденных значений найти наибольшее и наименьшее.