Файл: Сборник задач по физике. Грабцевич В. И. Импульс. Закон сохранения импульса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 717
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Mсосредоточена в ободе. Пренебрегая проскальзыванием нити по блоку, определить ускорение aгрузов. [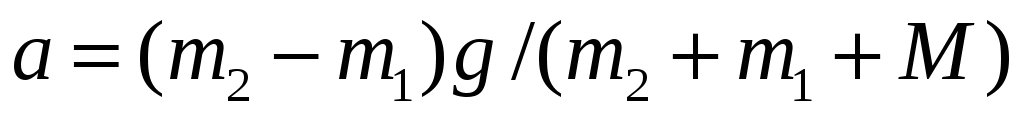
]
11.18. На концах и в середине невесомого стержня длиной l расположены одинаковые шарики. Стержень ставят вертикально и отпускают. Считая, что трение между плоскостью и нижним шариком отсутствует, найти скорость верхнего шарика в момент удара о горизонтальную поверхность. [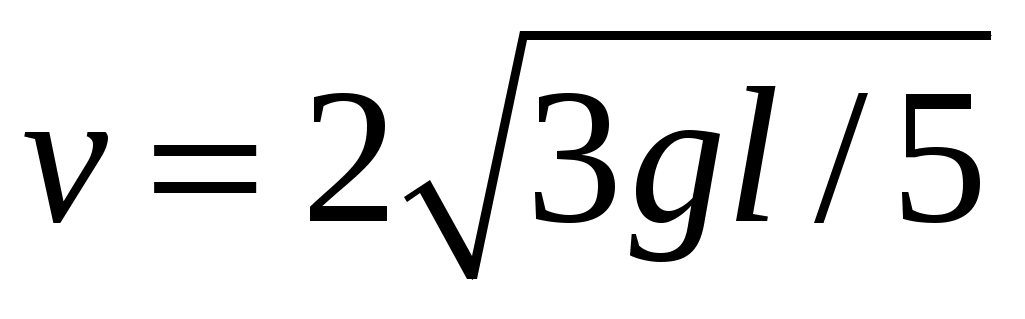
]
11.19. Гантелька длиной Lстоит в углу, образованном гладкими плоскостями. Нижний шарик гантельки смещают горизонтально на очень маленькое расстояние, и гантелька начинает двигаться. Найти скорость нижнего шарика в тот момент, когда верхний шарик оторвется от вертикальной плоскости. Масса шариков одинакова.
[
]
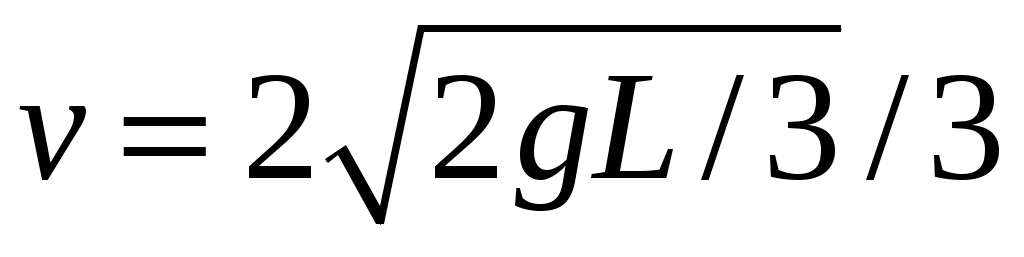11.20. На горизонтальной поверхности находится гладкая полусфера радиусом R. С верхней ее точки без начальной скорости соскальзывает тело. На какой высоте от основания сферы тело оторвется от ее поверхности. [H = 2R/3]
11.21. Тело массой m = 2 кг соскальзывает с горки высотой H = 4,5 м по наклонной поверхности, плавно переходящей в цилиндрическую поверхность радиусом R = 2м. Определить силу давления тела на цилиндрическую поверхность в ее верхней точке,если работа сил трения при движении тела до этой точки A = 40 Дж. [N = 10 H]
11.22. Тело массой m = 0,2 кг соскальзывает с высоты H = 8 м по наклонной плоскости, плавно переходящей в вертикальную петлю радиусом R = 2 м. Определить работу силы трения при движении тела до верхней точки петли, если давление тела на петлю в верхней точке N равно 2 Н.[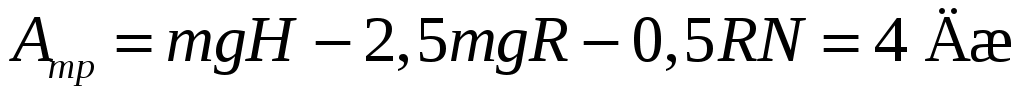
]
1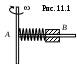
1.23. Гладкий легкий горизонтальный стержень AB может вращаться без трения вокруг вертикальной оси (рис. 11.1), проходящей через его конец A. На стержне находится небольшое тело массой m, соединенное невесомой пружиной длиной lo с концом A. Коэффициент жесткости пружины равен k. Какую работу надо совершить, чтобы эту систему медленно раскрутить до угловой скорости ? [
]
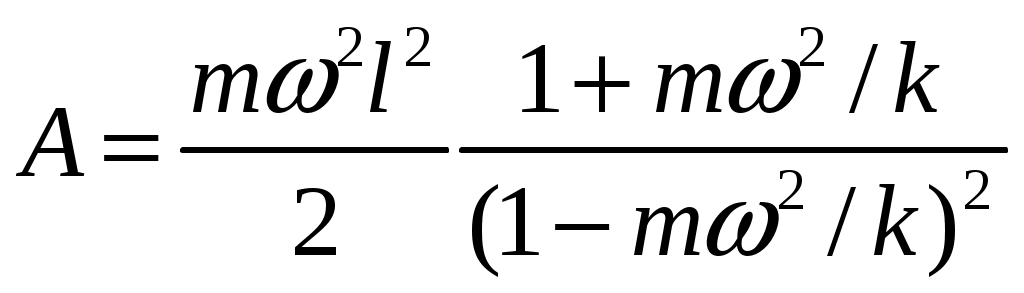11.24. Прикрепленный к вертикальной пружине груз медленно опускают до положения равновесия, причем пружина растягивается на длину xo. На сколько растянется пружина, если тому же грузу предоставить возможность падать свободно с такого положения, при котором пружина не растянута? Какой максимальной скорости достигнет при этом груз? Массой пружины пренебречь. [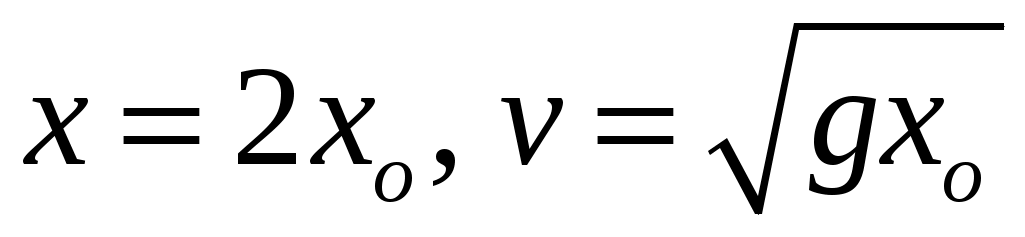
]
1
1.25. Груз массой m =1000 кгопускается с помощью лебедки с постоянной скоростью v = 4 м/с. Какова будет максимальная сила натяжения троса при внезапной остановке лебедки, если жесткость троса k = 5105 Н/м? [
]
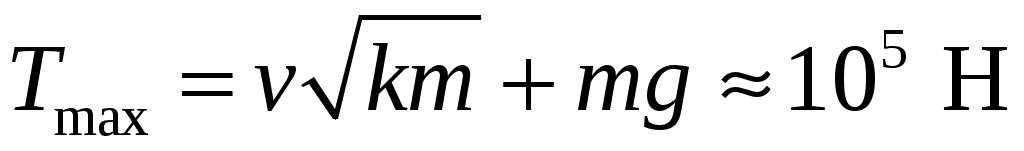11.26. Легкая пружина с жесткостью kстоит вертикально на столе (рис. 11.2). С высоты Hна нее падает небольшой шарик массой m.Какую максимальную скорость будет иметь шарик при своем движении вниз? Каково будет максимальное сжатие пружины?
[
]
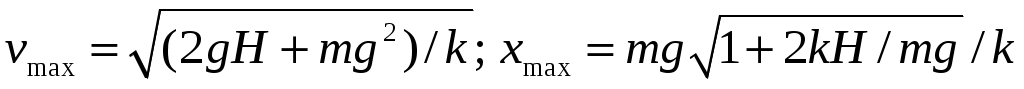11.27. Два груза массой m1 и m2 соединенные между собой пружиной, лежат на горизонтальном столе (рис. 11.3). Пружина в начальный момент не натянута. С какой минимальной силой Fнужно потянуть первый груз, чтобы при этом второй сдвинулся с места? Коэффициент трения между столом и грузом . [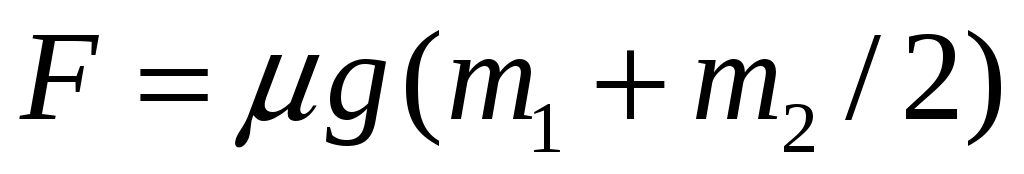
]
1
1.28. Телу, находящемуся на поверхности Земли, сообщена вертикальная скорость 6 км/с. Пренебрегая сопротивлением воздуха, найти максимальную высоту его подъема. Радиус Земли R3 = 6400 км. [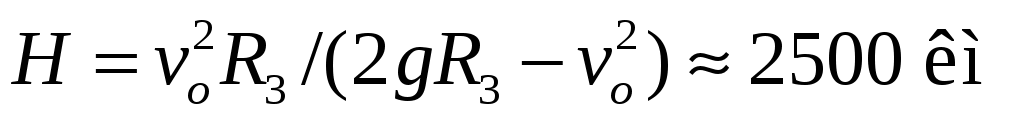
]
11.29. Определить скорость, которую необходимо сообщить телу, чтобы оно могло преодолеть силу притяжения Земли (вторую космическую скорость).
[
]
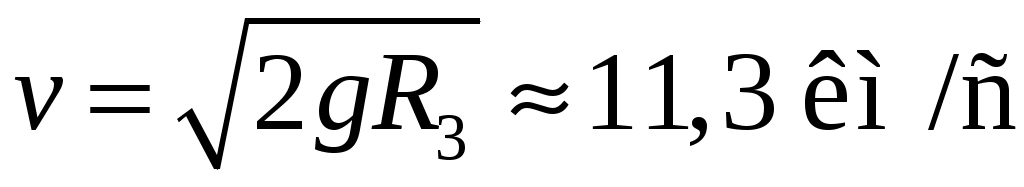11.30. Два одинаковых груза нужно поднять на крышу дома. Один рабочий решил поднимать груз на веревке вертикально вверх, второй – тянуть груз вверх по трапу, угол наклона которого к горизонту = 60
о, а коэффициент трения между грузом и трапом = 0,05. Во сколько раз отличаются работы, совершенные при подъеме грузов на крышу обоими рабочими? [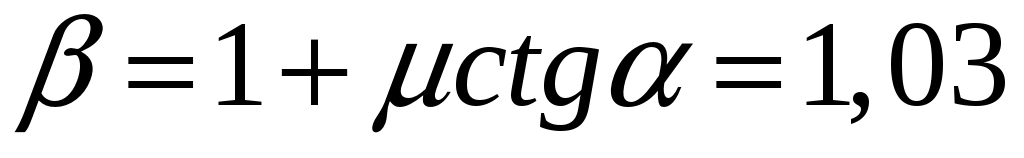
]
11.31. Кирпич, лежащий на краю крыши дома, толкнули вверх вдоль ската со скоростью v = 10 м/с. После упругого удара о конек кирпич соскользнул обратно и остановился на краю крыши. Найти коэффициент трения между кирпичом и поверхностью крыши, если конец находится на высоте h = 2,5 м от края крыши, а угол наклона крыши к горизонту = 30о. [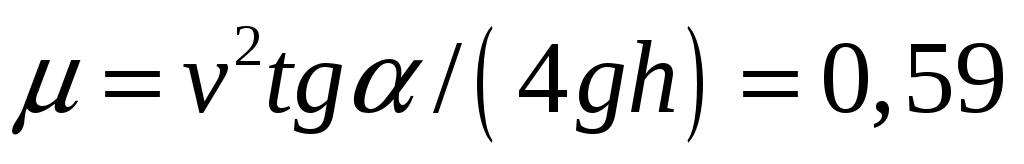
]
11.32. При броске тела от поверхности Земли под некоторым углом к горизонту была совершена работа A = 58,8 Дж. На каком расстоянии S от места бросания тело упало на землю, если его масса m = 1 кг, а максимальная высота подъема H = 3 м?
[
]
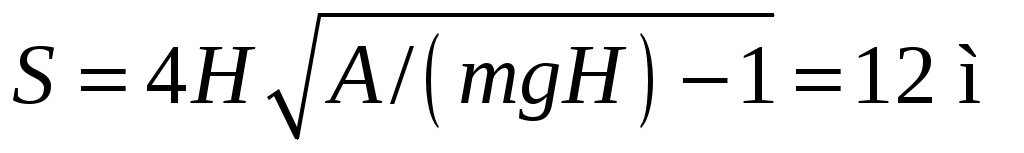11.33. Спутник запущен на круговую орбиту, проходящую на высоте h = 350 км над поверхностью Земли. Через некоторое время спутник перевели на другую круговую орбиту, радиус которой на h = 25 км меньше. На какую величину изменилась при этом кинетическая энергия спутника по отношению к первоначальному значению? [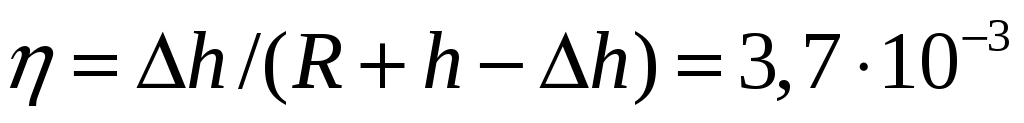
]
11.34. Брусок массой m = 1 кг покоится на горизонтальной шероховатой поверхности. К нему прикреплена пружина жесткости k = 20 Н/м. Какую работу A нужно совершить для того, чтобы сдвинуть с места брусок, растягивая пружину в горизонтальном направлении, если коэффициент трения между бруском и поверхностью = 0,2? [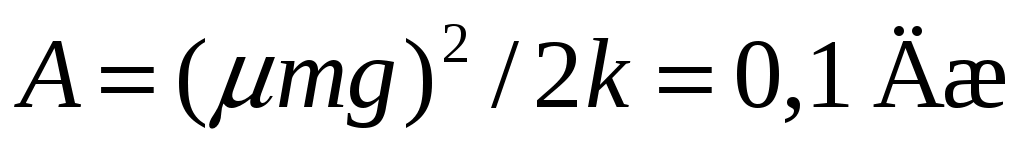
]
11.35. Шарик массой m = 100 г подвешен на нити длиной l = 1 м. Его приводят в движение так, что он обращается по окружности в горизонтальной плоскости, которая находится на расстоянии l/2 от точки подвеса. Какую работу нужно совершить для сообщения шарику такого движения? [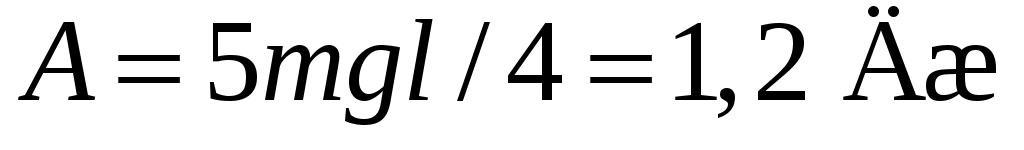
]
1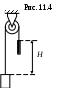
1.36. Начальное положение кабины лифта K и противовеса П изображено на рисунке 11.4. На какую величину U изменится потенциальная энергия системы при перемещении кабины вверх на расстояние
h = 10 м, если начальная разность уровней противовеса и кабины H = 15 м, масса кабины M = 1 т, масса противовеса m = 0,5 т, а масса единицы длины троса, соединяющего кабину с противовесом, = 10 кг/м. Ускорение свободного падения принять g = 10 м/с2.
[
]
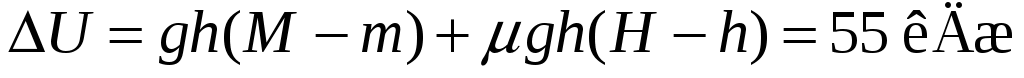11.37. На горизонтальном участке пути длиной L = 3 км скорость поезда увеличилась от v1 = 36 км/ч до v2 = 72 км/ч. Какое количество топлива m израсходовал двигатель локомотива на этом участке, если суммарная масса поезда и локомотива M = 1000 т, коэффициент трения = 0,005, удельная теплота сгорания топлива q = 42 МДж/кг, коэффициент полезного действия двигателя = 30 %.
[
]
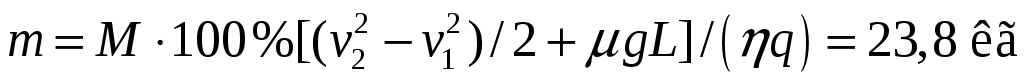Закон сохранения механической энергии и импульса.
12.1. Клин массой M = 0,5 кг с углом при основании = 30о покоится на гладкой горизонтальной плоскости. На наклонную поверхность клина ставят заводной автомобиль массой m = 0,1 кг и опускают без начальной скорости, после чего автомобиль начинает движение вверх по клину. Найдите скорость автомобиля относительно клина в момент, когда клин приобретет относительно плоскости скорость v = 2 см/с. [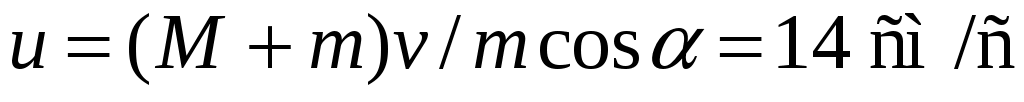
]
12.2. На прямолинейном горизонтальном участке пути стоят N = 5 отдельных вагонов. Промежутки между соседними вагонами одинаковы и равны L = 30 м. К крайнему вагону подкатывается еще один такой же вагон, имеющий скорость vo = 2 м/с. В результате N последовательных столкновений, в каждом из которых сталкивающиеся вагоны сцепляются вместе, все N + 1 вагонов соединяются в один состав. Найти время t между первым и последним столкновением. Силами сопротивления движению вагонов пренебречь. [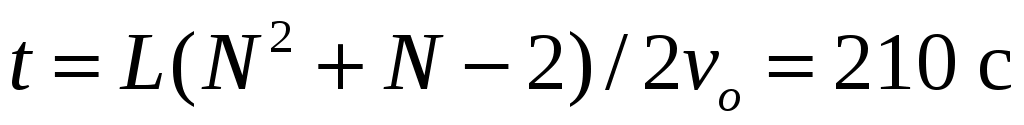
]
1
2.3. На гладком горизонтальном столе покоится «горка» (рис. 12.1), угол наклона которой плавно изменяется от некоторого значения до нуля. С вершины «горки» соскальзывает без трения небольшое тело массой m. Какова будет скорость тела после соскальзывания, если высота «горки» h, масса M. Трением между горкой и столом пренебречь. [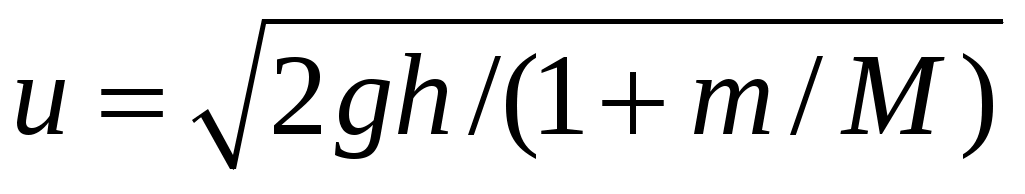
]
1
2.4. На пути тела A, скользящего по гладкому горизонтальному столу, находится незакрепленная «горка» высотой H. При какой минимальной скорости тело сможет преодолеть «горку»? Тело движется не отрываясь от горки. Трения нет. Масса горки M, масса тела m. [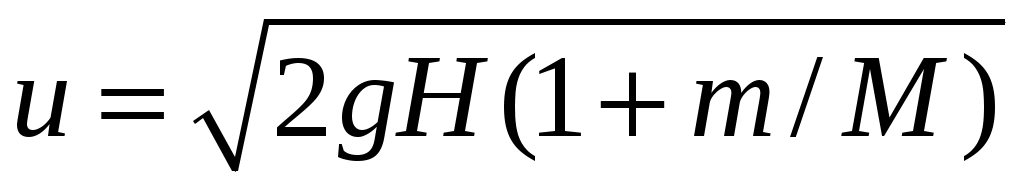
]
12.5. Преграда массой M = 10 кг, имеющая цилиндрическую поверхность с радиусом R = 0,2 м, расположена на горизонтальной плоскости. Тело массой m = 1 кг с начальной горизонтальной скоростью vo = 3 м/с, скользя, поднимается по цилиндрической поверхности. Определить скорость тела на высоте, равной радиусу R (в точке A). Трением пренебречь. [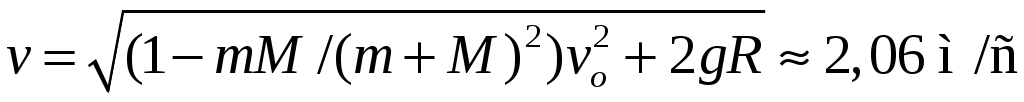
]
12.6. На гладкой горизонтальной поверхности около стенки стоит симметричный брусок массой m1 с углублением полусферической формы радиусом R (рис. 12.2). Из точки A без трения соскальзывает маленькая шайба массой m2. Найти максимальную скорость бруска при его последующем движении. [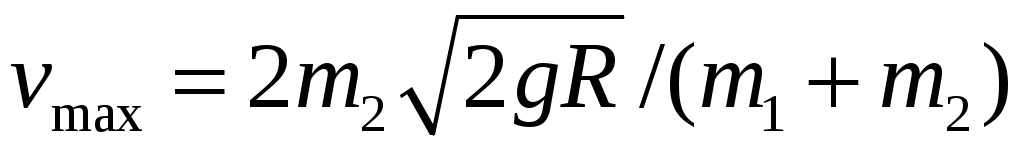
]
1
2
]11.18. На концах и в середине невесомого стержня длиной l расположены одинаковые шарики. Стержень ставят вертикально и отпускают. Считая, что трение между плоскостью и нижним шариком отсутствует, найти скорость верхнего шарика в момент удара о горизонтальную поверхность. [
]11.19. Гантелька длиной Lстоит в углу, образованном гладкими плоскостями. Нижний шарик гантельки смещают горизонтально на очень маленькое расстояние, и гантелька начинает двигаться. Найти скорость нижнего шарика в тот момент, когда верхний шарик оторвется от вертикальной плоскости. Масса шариков одинакова.
[
]11.20. На горизонтальной поверхности находится гладкая полусфера радиусом R. С верхней ее точки без начальной скорости соскальзывает тело. На какой высоте от основания сферы тело оторвется от ее поверхности. [H = 2R/3]
11.21. Тело массой m = 2 кг соскальзывает с горки высотой H = 4,5 м по наклонной поверхности, плавно переходящей в цилиндрическую поверхность радиусом R = 2м. Определить силу давления тела на цилиндрическую поверхность в ее верхней точке,если работа сил трения при движении тела до этой точки A = 40 Дж. [N = 10 H]
11.22. Тело массой m = 0,2 кг соскальзывает с высоты H = 8 м по наклонной плоскости, плавно переходящей в вертикальную петлю радиусом R = 2 м. Определить работу силы трения при движении тела до верхней точки петли, если давление тела на петлю в верхней точке N равно 2 Н.[
]1
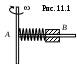1.23. Гладкий легкий горизонтальный стержень AB может вращаться без трения вокруг вертикальной оси (рис. 11.1), проходящей через его конец A. На стержне находится небольшое тело массой m, соединенное невесомой пружиной длиной lo с концом A. Коэффициент жесткости пружины равен k. Какую работу надо совершить, чтобы эту систему медленно раскрутить до угловой скорости ? [
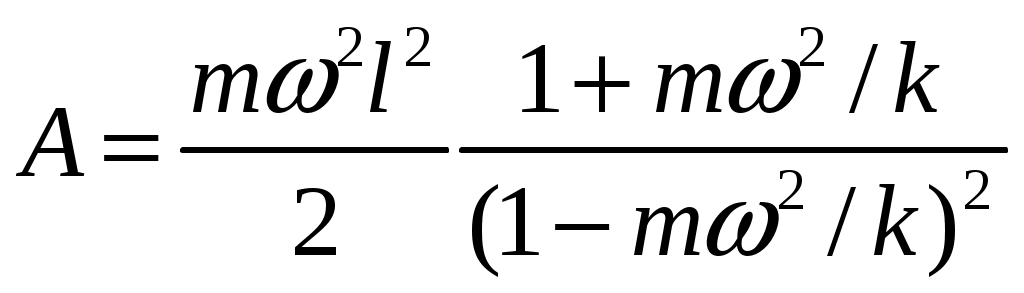]11.24. Прикрепленный к вертикальной пружине груз медленно опускают до положения равновесия, причем пружина растягивается на длину xo. На сколько растянется пружина, если тому же грузу предоставить возможность падать свободно с такого положения, при котором пружина не растянута? Какой максимальной скорости достигнет при этом груз? Массой пружины пренебречь. [
]1
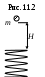1.25. Груз массой m =1000 кгопускается с помощью лебедки с постоянной скоростью v = 4 м/с. Какова будет максимальная сила натяжения троса при внезапной остановке лебедки, если жесткость троса k = 5105 Н/м? [ ]11.26. Легкая пружина с жесткостью kстоит вертикально на столе (рис. 11.2). С высоты Hна нее падает небольшой шарик массой m.Какую максимальную скорость будет иметь шарик при своем движении вниз? Каково будет максимальное сжатие пружины?
[
]11.27. Два груза массой m1 и m2 соединенные между собой пружиной, лежат на горизонтальном столе (рис. 11.3). Пружина в начальный момент не натянута. С какой минимальной силой Fнужно потянуть первый груз, чтобы при этом второй сдвинулся с места? Коэффициент трения между столом и грузом . [
]1
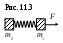1.28. Телу, находящемуся на поверхности Земли, сообщена вертикальная скорость 6 км/с. Пренебрегая сопротивлением воздуха, найти максимальную высоту его подъема. Радиус Земли R3 = 6400 км. [ ]11.29. Определить скорость, которую необходимо сообщить телу, чтобы оно могло преодолеть силу притяжения Земли (вторую космическую скорость).
[
]11.30. Два одинаковых груза нужно поднять на крышу дома. Один рабочий решил поднимать груз на веревке вертикально вверх, второй – тянуть груз вверх по трапу, угол наклона которого к горизонту = 60
о, а коэффициент трения между грузом и трапом = 0,05. Во сколько раз отличаются работы, совершенные при подъеме грузов на крышу обоими рабочими? [
]11.31. Кирпич, лежащий на краю крыши дома, толкнули вверх вдоль ската со скоростью v = 10 м/с. После упругого удара о конек кирпич соскользнул обратно и остановился на краю крыши. Найти коэффициент трения между кирпичом и поверхностью крыши, если конец находится на высоте h = 2,5 м от края крыши, а угол наклона крыши к горизонту = 30о. [
]11.32. При броске тела от поверхности Земли под некоторым углом к горизонту была совершена работа A = 58,8 Дж. На каком расстоянии S от места бросания тело упало на землю, если его масса m = 1 кг, а максимальная высота подъема H = 3 м?
[
]11.33. Спутник запущен на круговую орбиту, проходящую на высоте h = 350 км над поверхностью Земли. Через некоторое время спутник перевели на другую круговую орбиту, радиус которой на h = 25 км меньше. На какую величину изменилась при этом кинетическая энергия спутника по отношению к первоначальному значению? [
]11.34. Брусок массой m = 1 кг покоится на горизонтальной шероховатой поверхности. К нему прикреплена пружина жесткости k = 20 Н/м. Какую работу A нужно совершить для того, чтобы сдвинуть с места брусок, растягивая пружину в горизонтальном направлении, если коэффициент трения между бруском и поверхностью = 0,2? [
]11.35. Шарик массой m = 100 г подвешен на нити длиной l = 1 м. Его приводят в движение так, что он обращается по окружности в горизонтальной плоскости, которая находится на расстоянии l/2 от точки подвеса. Какую работу нужно совершить для сообщения шарику такого движения? [
]1
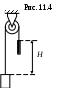1.36. Начальное положение кабины лифта K и противовеса П изображено на рисунке 11.4. На какую величину U изменится потенциальная энергия системы при перемещении кабины вверх на расстояние
h = 10 м, если начальная разность уровней противовеса и кабины H = 15 м, масса кабины M = 1 т, масса противовеса m = 0,5 т, а масса единицы длины троса, соединяющего кабину с противовесом, = 10 кг/м. Ускорение свободного падения принять g = 10 м/с2.
[
]11.37. На горизонтальном участке пути длиной L = 3 км скорость поезда увеличилась от v1 = 36 км/ч до v2 = 72 км/ч. Какое количество топлива m израсходовал двигатель локомотива на этом участке, если суммарная масса поезда и локомотива M = 1000 т, коэффициент трения = 0,005, удельная теплота сгорания топлива q = 42 МДж/кг, коэффициент полезного действия двигателя = 30 %.
[
]Закон сохранения механической энергии и импульса.
12.1. Клин массой M = 0,5 кг с углом при основании = 30о покоится на гладкой горизонтальной плоскости. На наклонную поверхность клина ставят заводной автомобиль массой m = 0,1 кг и опускают без начальной скорости, после чего автомобиль начинает движение вверх по клину. Найдите скорость автомобиля относительно клина в момент, когда клин приобретет относительно плоскости скорость v = 2 см/с. [
]12.2. На прямолинейном горизонтальном участке пути стоят N = 5 отдельных вагонов. Промежутки между соседними вагонами одинаковы и равны L = 30 м. К крайнему вагону подкатывается еще один такой же вагон, имеющий скорость vo = 2 м/с. В результате N последовательных столкновений, в каждом из которых сталкивающиеся вагоны сцепляются вместе, все N + 1 вагонов соединяются в один состав. Найти время t между первым и последним столкновением. Силами сопротивления движению вагонов пренебречь. [
]1
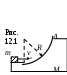2.3. На гладком горизонтальном столе покоится «горка» (рис. 12.1), угол наклона которой плавно изменяется от некоторого значения до нуля. С вершины «горки» соскальзывает без трения небольшое тело массой m. Какова будет скорость тела после соскальзывания, если высота «горки» h, масса M. Трением между горкой и столом пренебречь. [ ]1
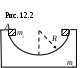2.4. На пути тела A, скользящего по гладкому горизонтальному столу, находится незакрепленная «горка» высотой H. При какой минимальной скорости тело сможет преодолеть «горку»? Тело движется не отрываясь от горки. Трения нет. Масса горки M, масса тела m. [ ]12.5. Преграда массой M = 10 кг, имеющая цилиндрическую поверхность с радиусом R = 0,2 м, расположена на горизонтальной плоскости. Тело массой m = 1 кг с начальной горизонтальной скоростью vo = 3 м/с, скользя, поднимается по цилиндрической поверхности. Определить скорость тела на высоте, равной радиусу R (в точке A). Трением пренебречь. [
]12.6. На гладкой горизонтальной поверхности около стенки стоит симметричный брусок массой m1 с углублением полусферической формы радиусом R (рис. 12.2). Из точки A без трения соскальзывает маленькая шайба массой m2. Найти максимальную скорость бруска при его последующем движении. [
]1
2