Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Методы оптимальных решений.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 05.12.2023

Просмотров: 172

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное

образовательное учреждение высшего образования

«Тульский государственный университет»

Институт права и управления

Кафедра «Финансы и менеджмент»


Утверждено на заседании кафедры

«Финансы и менеджмент»

«30» августа 2022 г., протокол № 1

З аведующий кафедрой

_________________________А.Л.Сабинина

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению курсовой работы

по дисциплине (модулю)

«Методы оптимальных решений»

основной профессиональной образовательной программы

высшего образования – программы бакалавриата

по направлению подготовки

38.03.01 «Экономика»
с направленностью (профилем)

Финансы и кредит


Форма(ы) обучения: очно-заочная и заочная
Идентификационный номер образовательной программы: 380301-02-22


Тула 2021 год

Разработчик(и) методических указаний
___ Гучек Н. Е., доцент, к.т.н.___________ __ _ (ФИО, должность, ученая степень, ученое звание) (подпись)
__________________________________________ __________

(ФИО, должность, ученая степень, ученое звание) (подпись)

Содержание

Содержание 3

1. Цель и задачи выполнения курсовой работы 3

2. Основные требования к курсовой работе 4

2.1. Тематика курсовой работы 4

2.2. Задание курсовой работы 4

2.2.1. Задача оптимального распределения ресурсов 5

2.2.2. Транспортная задача 5

2.2.3. Задача динамического программирования 6

2.3. Исходные данные к курсовой работе 6

2.3.1. Задача оптимального распределения ресурсов 6

2.3.3. Задача динамического программирования 10

2.4. Объем курсовой работы 14

2.5. Работа над курсовой работой 14

2.6. Защита курсовой работы 14

3. Методические указания к работе над курсовой работой 15

3.1. План построения и содержание разделов пояснительной записки к курсовой работе 15

3.2. Методические указания по выполнению отдельных разделов курсовой работы 15

3.3. Оформление пояснительной записки 64

Список использованных источников 64

Список использованных источников 64


1. Цель и задачи выполнения курсовой работы

Целью выполнения типового расчета по дисциплине «Методы оптимальных решений» является овладение студентами математическими методами решения экономических задач.

Задачи выполнения типового расчета:

- научиться строить экономико-математические модели;

- освоить симплекс-метод табличного решения задачи линейного программирования
;

- освоить двойственный симплекс-метод решения задачи линейного программирования;

- освоить метод потенциалов решения транспортной задачи;

- освоить методику решения антагонистических игр;

- освоить методику решения задачи динамического программирования.

2. Основные требования к курсовой работе

2.1. Тематика курсовой работы

1. Обоснование принятия оптимальных решений для автомобилестроительного предприятия.

2. Обоснование принятия оптимальных решений для молочного комбината.

3. Обоснование принятия оптимальных решений для химического производства.

4. Обоснование принятия оптимальных решений для предприятия по производству компьютерной техники.

5. Обоснование принятия оптимальных решений для обувной фабрики.

6. Обоснование принятия оптимальных решений для швейной фабрики.

7. Обоснование принятия оптимальных решений для автотранспортного предприятия (грузовые перевозки).

8. Обоснование принятия оптимальных решений для предприятия оптовой торговли продовольственными товарами.

9. Обоснование принятия оптимальных решений для предприятия цветной металлургии.

10. Обоснование принятия оптимальных решений для предприятия сервисного обслуживания (химчистка).

11. Обоснование принятия оптимальных решений для мясокомбината.

12. Обоснование принятия оптимальных решений для хлебозавода.

13. Обоснование принятия оптимальных решений для кондитерской фабрики.

14. Обоснование принятия оптимальных решений для предприятия по ремонту компьютерной техники.

15. Обоснование принятия оптимальных решений для металлургического предприятия.

2.2. Задание курсовой работы

В рамках курсовой работы студенты в соответствии с вариантом должны решить три задачи:

1. Задача оптимального распределения ресурсов.

2. Транспортная задача.

3.Задача динамического программирования.

2.2.1. Задача оптимального распределения ресурсов

Организация имеется возможность выпускать n видов изделий П1, П2, П3,…, Пn. При их изготовлении используются ресурсы Р1, Р2, Р3,…, Рm. Размеры допустимых затрат ресурсов ограничены соответственно величинами
b1, b2, b3, …, bm. Расход ресурса i-го вида (i = 1, 2,…, m) на единицу изделия j-го вида (j = 1, 2,…, n) составляет aij ден. ед. Цена единицы продукции j-го вида равна сj. Требуется найти оптимальный план выпуска изделий, который обеспечивал бы организации максимальный доход.

Обязательные требования к решению задачи.

1. Построить экономико-математическую модель задачи распределения ресурсов.

2. Построить двойственную задачу к задаче распределения ресурсов. Ввести соответствие переменных прямой и двойственной задачи.

3. Найти оптимальное решение прямой и двойственной задач линейного программирования, пояснить экономический смысл всех переменных, участвующих в решении.

4. Найти границы изменения дефицитных ресурсов, в пределах которых не изменится структура оптимального плана.

5. Уточнить значения недефицитных ресурсов, при которых оптимальный план не изменится.

6. Найти границы изменения цены изделия, попавших в оптимальный план производства, в пределах которых оптимальный план не изменится.

7. Определить величину ∆bs ресурса Рs, введением которого в производство можно компенсировать убыток и сохранить максимальный доход на прежнем уровне (ресурсы предполагаются взаимно заменяемыми), получаемый при исключении из производства ∆br единиц ресурса Рr что вызывает уменьшение максимального дохода на ∆rfomax ед.

8. Оценить целесообразность приобретения ∆bk единиц ресурса Рk по цене сk за единицу.

9. Установить, целесообразно ли выпускать новое изделие П4, на единицу которого ресурсы Р1, Р2, Р3 расходуются в количествах a14, a24, a34 единиц, а цена единицы изделия составляет с4 денежных единиц.

10. Решить прямую и двойственную задачи линейного программирования в среде Microsoft Exсel, приложить отчеты, провести вычислительный эксперимент для уточнения границ изменения ресурсов и цен.

2.2.2. Транспортная задача

На трех базах (пунктах отправления) A1, A2, A3находится однородный груз в количествах
, соответственно равных а1, а2 и а3 единицам. Этот груз требуется перевести в три пункта назначения B1, B2, B3соответственно в количествах b1, b2 и b3. единиц. Стоимость перевозки единицы груза из i-го пункта отправления в j-й пункт назначения составляет cij денежных единиц. Определить оптимальный план перевозок, при котором общая стоимость перевозок будет минимальной.

Обязательные требования к решению задачи.

1. Проверить разрешимость транспортной задачи. Если задача не разрешима, свести ее к закрытой задаче введением фиктивного пункта отправления (поставщика) или пункта назначения (потребителя).

2. Построить экономико-математическую модель транспортной задачи.

3. Построить двойственную задачу.

4. Найти начальное решение транспортной задачи и проверить его на вырожденность.

5. Решить транспортную задачу методом потенциалов.

6. Решить транспортную задачу в среде Microsoft Exсel, приложить отчет.

2.2.3. Задача динамического программирования
На развитие трех предприятий выделено S млн. руб. Известна эффективность капитальных вложений xi в каждое j-е предприятие, заданная таблично значением нелинейной функции fj(xi), где 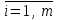, , 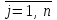n – количество предприятий, m – количество возможных сумм капитальных вложений.

Необходимо распределить выделенные средства между предприятиями таким образом, чтобы получить максимальный суммарный доход.

2.3. Исходные данные к курсовой работе

2.3.1. Задача оптимального распределения ресурсов


Обозначения
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

b1
300
300
350
650
300
300
300
450
300
600
300
650
300
130
300

b2
500
500
250
560
550
150
300
500
450
500
250
500
450
250
200

b3
400
400
500
430
400
400
520
550
400
400
500
300
400
140
350

a11
2
5
3
1
1
1
3
1
2
1
3
1
1
1
3

a12
3
3
1
4
3
3
1
4
3
3
1
4
3
3
1

a13
2
3
2
2
2
2
2
5
2
2
2
2
2
2
2

a21
2
2
2
4
2
2
2
4
2
2
2
4
2
2
2

a22
3
3
3
6
3
3
3
6
3
3
3
6
3
3
3

a23
1
1
4
8
1
1
4
8
1
1
4
8
1
1
4

a31
3
3
1
4
3
3
1
1
3
3
1
1
3
3
1

a32
1
1
2
5
1
1
2
1
1
1
2
4
1
1
2

Обозначения
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

a33
2
2
6
9
2
2
6
9
2
2
6
9
2
2
6

c1
30
30
40
30
30
30
40
30
30
30
40
35
30
30
40

c2
40
40
50
60
40
40
60
40
40
40
50
60
40
40
60

c3
30
10
80
50
35
10
30
50
35
10
80
40
15
10
80

r
1
1
2
3
1
1
2
2
1
1
2
3
1
1
2

∆br
0,5
0,5
2
0,1
0,5
0,2
2
0,1
0,5
0,2
2
0,1
0,5
0,2
2

s
3
2
3
1
3
2
3
1
3
2
3
1
3
2
3

k
3
3
1
2
3
3
1
2
3
3
1
2
3
3
1

∆bk
0,3
0,2
0,5
0,5
0,2
0,2
0,5
0,5
0,2
0,2
0,5
0, 1
0,3
0,2
0,5

ck
1,5
15
12
24
1,5
15
12
24
1,5
15
12
24
1,5
15
12

ℓ
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4

a1ℓ
2
2
3
4
2
2
3
4
2
2
3
4
2
2
3

a2ℓ
1
3
2
4
1
3
2
4
1
3
2
4
1
3
2

a3ℓ
2
1
4
2
2
1
4
2
2
1
4
2
2
1
4

cℓ
45
50
60
70
45
35
60
70
45
35
60
70
45
35
60

Смотрите также файлы