Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Методы оптимальных решений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 174
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, n – количество предприятий, m – количество возможных сумм капитальных вложений.
Необходимо распределить выделенные средства между предприятиями таким образом, чтобы получить максимальный суммарный доход.
Исходные данные варианта 0:
Математическая модель задачи.
Определить Х* = (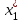 ,
,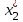 , …,
, …, 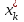 , …,
, …, 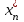 ), обеспечивающий максимум целевой функции
), обеспечивающий максимум целевой функции
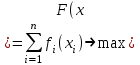
и удовлетворяющий условиям
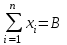 ,
,
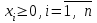
Математическая модель задачи варианта 0:
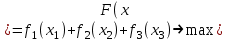
при ограничениях:
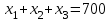 ,
,
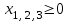 .
.
Условная оптимизация.
Максимально возможный доход, который может быть получен с предприятий (с
k-го по n-е), определяется с помощью функции Беллмана:
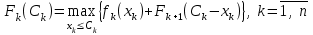 ,
,
где Сk – количество средств, инвестируемых в k-е предприятие, 0≤ Сk ≤ В.
На первом шаге условной оптимизации при k = n функция Беллмана представляет собой прибыль только с n-го предприятия. При этом на его инвестирование может остаться количество средств Сn, 0 ≤ Сn ≤ В. Чтобы получить максимум прибыли с этого предприятия, можно вложить в него все эти средства, т.е. Fn(Сn) = fn(Сn) и хn = Сn.
Для упрощения расчетов предполагаем, что распределение средств осуществляется в целых числах xi = {0, 100, 200, 300, 400, 500, 600, 700} тыс. руб.
Решение.
I этап. Условная оптимизация.
1-й шаг: k = 3.
Таблица 1
В шапке таблицы отражены варианты значений капиталовложений х3, которые могут быть предоставлены третьему предприятию. В столбце C3 отражены варианты значений капиталовложений, которые могут быть выделены всем трем предприятиям в совокупности.
Предположим, что все средства в количестве x3 = 700 тыс. руб. отданы третьему предприятию. В этом случае максимальный доход составит f3(x3) = 700 тыс. руб., следовательно: F3(C3) = f3(x3) и x3= C3.
2-й шаг: k = 2. Определяем оптимальную стратегию при распределении денежных средств между вторым и третьим предприятиями. При этом рекуррентное соотношение Беллмана имеет вид:
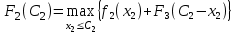 .
.
Представим в таблице расчет функции Беллмана.
Таблица 2
В шапке таблицы отражены варианты значений капиталовложений х2, которые могут быть предоставлены второму предприятию при условии, что часть средств выделяется третьему предприятию. В клетках таблицы первое слагаемое – это возможный прирост выпуска продукции второго предприятия f2(х2) в результате освоения капиталовложений х2; второе слагаемое – значение функции Беллмана, полученной на предыдущем шаге F3(C2 – х2), т.е. возможный прирост выпуска продукции третьего предприятия, если ему будет выделена оставшаяся часть капиталовложений, определяемая как C2 – х2.
Например, рассуждая формально, если при общей величине капиталовложений C2 = 0 второму предприятию выделяется х2 = 0, то прирост продукции составляет f2(0) = 0, а значение функции Беллмана из табл.1 составит: F3(0 – 0) = 0. Поэтому в клетке табл. 2 (0, 0) отражается сумма 0+0.
При общей величине капиталовложений C2 = 100 тыс. руб. возможны уже два варианта распределения средств между вторым и третьим предприятием:
1) второму предприятию ничего не выделяется, т.е. х2 = 0 и прирост продукции составляет f2(0) = 0. В этом случае значение функции Беллмана из табл. 1 составит F3(100 – 0) = F3(100) = 40 тыс. руб., т.е. вся сумма C2 = 100 тыс. руб. выделена третьему предприятию, поэтому суммарный прирост продукции составит 0+40, отражаемый в клетке (100, 0).
2) второму предприятию может быть выделено х2 = 100 тыс. руб., прирост продукции второго предприятия составляет f2(100) = 50 тыс. руб. В этом случае значение функции Беллмана из табл. 1 составит F3(100 – 100) = F3(0) = 0, т.е. вся сумма C2 = 100 тыс. руб. выделена второму предприятию, поэтому суммарный прирост продукции составит 50+0, отражаемый в клетке (100, 100).
Рассуждая аналогично, заполняются все строки табл. 2.
Максимальная сумма по каждой строке вносится в колонку F2(C2), одновременно в колонку вносят соответствующие максимальным суммам значения х2 из шапки табл. 2.
вносят соответствующие максимальным суммам значения х2 из шапки табл. 2.
Например, в строке C
2 = 100 максимальная сумма 160 не единственная, следовательно, F2(100) = 50, ему соответствует значение х2 = 100, следовательно, =100. В строке C2 = 500 максимальная сумма единственная 50, следовательно, F2(500) = 160, ему соответствуют значения х2 = 100, х2 = 400, х2 = 500, следовательно,
=100. В строке C2 = 500 максимальная сумма единственная 50, следовательно, F2(500) = 160, ему соответствуют значения х2 = 100, х2 = 400, х2 = 500, следовательно,  =100/400/500.
=100/400/500.
3-й шаг: k = 1. Определяем оптимальную стратегию при распределении денежных средств между первым и двумя другими предприятиями, используя следующую формулу для расчета суммарного дохода:
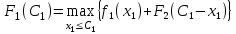 ,
,
на ее основе составлена табл. 3.
В шапке таблицы отражены варианты значений капиталовложений х1, которые могут быть предоставлены первому предприятию при условии, что часть средств выделяется второму и третьему предприятию. В клетках таблицы первое слагаемое – это возможный прирост выпуска продукции первого предприятия f1(х1) в результате освоения капиталовложений х1; второе слагаемое – значение функции Беллмана, полученной на предыдущем шаге F2(C1–х1), т.е. возможный прирост выпуска продукции второго и третьего предприятий, если им будет выделена оставшаяся часть капиталовложений, определяемая как C1 – х1.
Таблица 3
Необходимо распределить выделенные средства между предприятиями таким образом, чтобы получить максимальный суммарный доход.
Исходные данные варианта 0:
| Объем капиталовложений xi (тыс. руб.) | Прирост выпуска продукции fj(xi) в зависимости от объема капиталовложений (тыс. руб.) | ||
| предприятие 1 | предприятие 2 | предприятие 3 | |
| 0 | 0 | 0 | 0 |
| 100 | 30 | 50 | 40 |
| 200 | 50 | 70 | 50 |
| 300 | 70 | 90 | 80 |
| 400 | 100 | 120 | 110 |
| 500 | 150 | 160 | 150 |
| 600 | 190 | 190 | 180 |
| 700 | 210 | 220 | 230 |
Математическая модель задачи.
Определить Х* = (
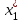 ,
,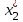 , …,
, …, 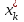 , …,
, …, 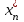 ), обеспечивающий максимум целевой функции
), обеспечивающий максимум целевой функции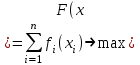
и удовлетворяющий условиям
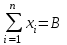 ,
,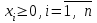
Математическая модель задачи варианта 0:
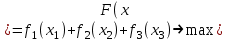
при ограничениях:
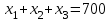 ,
,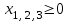 .
.Условная оптимизация.
Максимально возможный доход, который может быть получен с предприятий (с
k-го по n-е), определяется с помощью функции Беллмана:
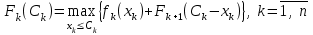 ,
,где Сk – количество средств, инвестируемых в k-е предприятие, 0≤ Сk ≤ В.
На первом шаге условной оптимизации при k = n функция Беллмана представляет собой прибыль только с n-го предприятия. При этом на его инвестирование может остаться количество средств Сn, 0 ≤ Сn ≤ В. Чтобы получить максимум прибыли с этого предприятия, можно вложить в него все эти средства, т.е. Fn(Сn) = fn(Сn) и хn = Сn.
Для упрощения расчетов предполагаем, что распределение средств осуществляется в целых числах xi = {0, 100, 200, 300, 400, 500, 600, 700} тыс. руб.
Решение.
I этап. Условная оптимизация.
1-й шаг: k = 3.
Таблица 1
| x3 C3 | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | F3(C3) | 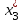 |
| 0 | 0 | | | | | | | | 0 | 0 |
| 100 | | 40 | | | | | | | 40 | 100 |
| 200 | | | 50 | | | | | | 50 | 200 |
| 300 | | | | 80 | | | | | 80 | 300 |
| 400 | | | | | 110 | | | | 110 | 400 |
| 500 | | | | | | 150 | | | 150 | 500 |
| 600 | | | | | | | 180 | | 180 | 600 |
| 700 | | | | | | | | 230 | 230 | 700 |
В шапке таблицы отражены варианты значений капиталовложений х3, которые могут быть предоставлены третьему предприятию. В столбце C3 отражены варианты значений капиталовложений, которые могут быть выделены всем трем предприятиям в совокупности.
Предположим, что все средства в количестве x3 = 700 тыс. руб. отданы третьему предприятию. В этом случае максимальный доход составит f3(x3) = 700 тыс. руб., следовательно: F3(C3) = f3(x3) и x3= C3.
2-й шаг: k = 2. Определяем оптимальную стратегию при распределении денежных средств между вторым и третьим предприятиями. При этом рекуррентное соотношение Беллмана имеет вид:
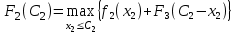 .
.Представим в таблице расчет функции Беллмана.
Таблица 2
| x2 C2 | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | F2(C2) |  |
| 0 | 0+0 | | | | | | | | 0 | 0 |
| 100 | 0+40 | 50+0 | | | | | | | 50 | 100 |
| 200 | 0+50 | 50+40 | 70+0 | | | | | | 90 | 100 |
| 300 | 0+80 | 50+50 | 70+40 | 90+0 | | | | | 110 | 200 |
| 400 | 0+110 | 50+80 | 70+50 | 90+40 | 120+0 | | | | 130 | 100/300 |
| 500 | 0+150 | 50+110 | 70+80 | 90+50 | 120+40 | 160+0 | | | 160 | 100/400/500 |
| 600 | 0+180 | 50+150 | 70+110 | 90+80 | 120+50 | 160+40 | 190+0 | | 200 | 100/500 |
| 700 | 0+230 | 50+180 | 70+150 | 90+110 | 120+80 | 160+50 | 190+40 | 220+0 | 230 | 0/600 |
В шапке таблицы отражены варианты значений капиталовложений х2, которые могут быть предоставлены второму предприятию при условии, что часть средств выделяется третьему предприятию. В клетках таблицы первое слагаемое – это возможный прирост выпуска продукции второго предприятия f2(х2) в результате освоения капиталовложений х2; второе слагаемое – значение функции Беллмана, полученной на предыдущем шаге F3(C2 – х2), т.е. возможный прирост выпуска продукции третьего предприятия, если ему будет выделена оставшаяся часть капиталовложений, определяемая как C2 – х2.
Например, рассуждая формально, если при общей величине капиталовложений C2 = 0 второму предприятию выделяется х2 = 0, то прирост продукции составляет f2(0) = 0, а значение функции Беллмана из табл.1 составит: F3(0 – 0) = 0. Поэтому в клетке табл. 2 (0, 0) отражается сумма 0+0.
При общей величине капиталовложений C2 = 100 тыс. руб. возможны уже два варианта распределения средств между вторым и третьим предприятием:
1) второму предприятию ничего не выделяется, т.е. х2 = 0 и прирост продукции составляет f2(0) = 0. В этом случае значение функции Беллмана из табл. 1 составит F3(100 – 0) = F3(100) = 40 тыс. руб., т.е. вся сумма C2 = 100 тыс. руб. выделена третьему предприятию, поэтому суммарный прирост продукции составит 0+40, отражаемый в клетке (100, 0).
2) второму предприятию может быть выделено х2 = 100 тыс. руб., прирост продукции второго предприятия составляет f2(100) = 50 тыс. руб. В этом случае значение функции Беллмана из табл. 1 составит F3(100 – 100) = F3(0) = 0, т.е. вся сумма C2 = 100 тыс. руб. выделена второму предприятию, поэтому суммарный прирост продукции составит 50+0, отражаемый в клетке (100, 100).
Рассуждая аналогично, заполняются все строки табл. 2.
Максимальная сумма по каждой строке вносится в колонку F2(C2), одновременно в колонку
 вносят соответствующие максимальным суммам значения х2 из шапки табл. 2.
вносят соответствующие максимальным суммам значения х2 из шапки табл. 2.Например, в строке C
2 = 100 максимальная сумма 160 не единственная, следовательно, F2(100) = 50, ему соответствует значение х2 = 100, следовательно,
 =100. В строке C2 = 500 максимальная сумма единственная 50, следовательно, F2(500) = 160, ему соответствуют значения х2 = 100, х2 = 400, х2 = 500, следовательно,
=100. В строке C2 = 500 максимальная сумма единственная 50, следовательно, F2(500) = 160, ему соответствуют значения х2 = 100, х2 = 400, х2 = 500, следовательно,  =100/400/500.
=100/400/500.3-й шаг: k = 1. Определяем оптимальную стратегию при распределении денежных средств между первым и двумя другими предприятиями, используя следующую формулу для расчета суммарного дохода:
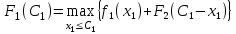 ,
, на ее основе составлена табл. 3.
В шапке таблицы отражены варианты значений капиталовложений х1, которые могут быть предоставлены первому предприятию при условии, что часть средств выделяется второму и третьему предприятию. В клетках таблицы первое слагаемое – это возможный прирост выпуска продукции первого предприятия f1(х1) в результате освоения капиталовложений х1; второе слагаемое – значение функции Беллмана, полученной на предыдущем шаге F2(C1–х1), т.е. возможный прирост выпуска продукции второго и третьего предприятий, если им будет выделена оставшаяся часть капиталовложений, определяемая как C1 – х1.
Таблица 3
| x1 C1 | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | F1(C1) |  |
| 0 | 0+0 | | | | | | | | 0 | 0 |
| 100 | 0+50 | 30+0 | | | | | | | 50 | 0 |
| 200 | 0+90 | 30+50 | 50+0 | | | | | | 90 | 0 |
| 300 | 0+110 | 30+90 | 50+50 | 70+0 | | | | | 120 | 100 |
| 400 | 0+130 | 30+110 | 50+90 | 70+50 | 100+0 | | | | 140 | 100/200 |
| 500 | 0+160 | 30+130 | 50+110 | 70+90 | 100+50 | 150+0 | | | 160 | 0/100/200/300 |
| 600 | 0+200 | 30+160 | 50+130 | 70+110 | 100+90 | 150+50 | 190+0 | | 200 | 100/500 |
| 700 | 0+230 | 30+200 | 50+160 | 70+130 | 100+110 | 150+90 | 190+50 | 210+0 | 240 | 500/600 |