Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Методы оптимальных решений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 176
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
+ v3 c13 = 0 + 1 – 7 = –6 < 0,
14 = u1 + v4 c14 = 0 + 5 – 5 = 0,
21 = u2 + v1 c21 = – 3 + 6 – 10 = –7 < 0,
23 = u2 + v3 c23 = – 3 + 1 – 6 = –8 < 0,
24 = u2 + v4 c24 = – 3 + 5 – 9 = –7 < 0,
31 = u3 + v1 c31 = 4 + 6 – 13 = –3 < 0,
34 = u3 + v4 c34 = 4 + 5 – 7 = 2 > 0,
42 = u4 + v2 c42 = – 1 + 10 – 10 = –1 < 0,
43 = u4 + v3 c43 = – 1 + 1 – 6 = –6 < 0.
Результаты расчета представлены в распределительной таблице:
Клетка (3, 4) имеет положительную оценку 34 = 2 > 0, следовательно, решение Х1 не оптимальное, а для клетки строим новый цикл: 0*5
141200* (все вершины цикла, кроме первой, находятся в занятых клетках, углы прямые, число вершин четное). У вершин цикла с соответствующими значениями поставок по правилу чередования знаков ставим знаки (+) и (–), начиная со свободной клетки. У вершин со знаком (–) выбираем минимальный груз = min[14, 20, 5] = 5.
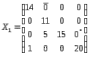
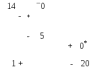
Его прибавляем к грузам, стоящим у положительных вершин, и отнимаем от грузов, стоящих у отрицательных вершин. Получаем новый цикл:
Получили новое решение задачи (план перевозок):
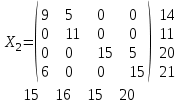
Справа и внизу матрицы проведена проверка: исходные данные запасов и потребностей в результате перераспределения поставок не изменились.
Значение целевой функции:
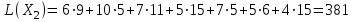(ед.).
Значение целевой функции уменьшилось на 10 ед.
Проверка решения Х2 на оптимальность. Расчет потенциалов для занятых клеток: u1 = 0;
клетка (1, 1): v1 = c11 – u1 = 6 – 0 = 6;
клетка (4, 1): u4 = c41 – v1 = 5 – 6 = 1;
клетка (1, 2): v2 = c12 – u1 = 10 – 0 = 10;
клетка (2, 2): u2 = c22 – v2 = 7 – 10 = 3;
клетка (4, 4): v4 = c44 – u4 = 4 – (1) = 5;
клетка (3, 4): u3 = c34 – v4 = 7 – 5 = 2;
клетка (3, 3): v3 = c33 – u3 = 5 – 2 = 3;
Расчет оценок свободных клеток:
13 = u1 + v3 c13 = 0 + 3 – 7 = –4 < 0,
14 = u1 + v4 c14 = 0 + 5 – 5 = 0,
21 = u2 + v1 c21 = – 3 + 6 – 10 = –7 < 0,
23 = u2 + v3 c23 = – 3 + 3 – 6 = –6 < 0,
24 = u2 + v4 c24 = – 3 + 5 – 9 = –7 < 0,
31 = u3 + v1 c31 = 2 + 6 – 13 = –5 < 0,
32 = u3 + v2 c32 = 2 + 10 – 14 = –2 < 0,
42 = u4 + v2 c42 = – 1 + 10 – 10 = –1 < 0,
43 = u4 + v3 c43 = – 1 + 3 – 6 = –4 < 0.
Результаты расчета представлены в распределительной таблице:
Все оценки свободных клеток положительные, следовательно, решение Х2 оптимально.
Оценка клетки (1, 4) 14 = 0 означает, что задача имеет альтернативные решения.
Методика нахождения альтернативного решения
Для нахождения альтернативного решения для клетки с нулевой оценкой строят еще один цикл перераспределения поставок по тем же правилам, что и при улучшении решения. Проверка оптимальности решения для альтернативного решения не производится. Следует проверить значение целевой функции, соответствующее альтернативному решению: оно должно совпадать со значением целевой функции, соответствующим первому оптимальному решению.
Найдем одно из альтернативных решений. Для этого для клетки с нулевой оценкой строим еще один цикл: 0*96150* (все вершины цикла, кроме первой, находятся в занятых клетках, углы прямые, число вершин четное). У вершин цикла с соответствующими значениями поставок по правилу чередования знаков ставим знаки (+) и (–), начиная со свободной клетки. У вершин со знаком (–) выбираем минимальный груз = min[9, 15] = 9.
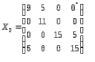
Его прибавляем к грузам, стоящим у положительных вершин, и отнимаем от грузов, стоящих у отрицательных вершин. Получаем новый цикл:
Получили альтернативное решение задачи (план перевозок):
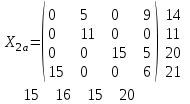
Значение целевой функции:
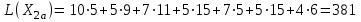(ед.).
Значение целевой функции альтернативного решения совпало со значением целевой функции первого оптимального решения транспортной задачи.
Таким образом, решение транспортной задачи:
, 
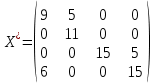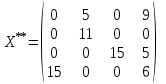, L(X*) = 381(ед.).
5. Решение транспортной задачи в среде Microsoft Exсel
Ввод исходных данных (в области C3:F6 – тарифы на перевозку продукции; в столбце G3:G6 – запасы; в ячейках С7
, D7, E7, F7 – потребности).
В области решения в ячейке G10 введите формулу стоимости перевозок:
=СУММПРОИЗВ(C12:F15;C3:F6). Для этого необходимо нажать на значок f(x) на панели инструментов, выбрать математическую функцию СУММПРОИЗВ и ввести два массива C12:F15 и C3:F6. Далее в области C12:F15 проставьте любое первоначальное решение (например, единицы)/
В ячейке С16 записывается формула: =СУММ(C12:C14), т.е. сумма значений по столбцу (можно выделить значения столбца и нажать на знак автосуммы Σ на панели инструментов). Аналогично в D16, E16, F16. Автоматически суммируются значения по столбцам.
В ячейке G12 записывается формула: =СУММ(C12:F12), т.е. сумма значений по строке (можно выделить значения строки и нажать на знак автосуммы Σ на панели инструментов). Аналогично в G13, G14, G15. Автоматически суммируются значения по строкам:
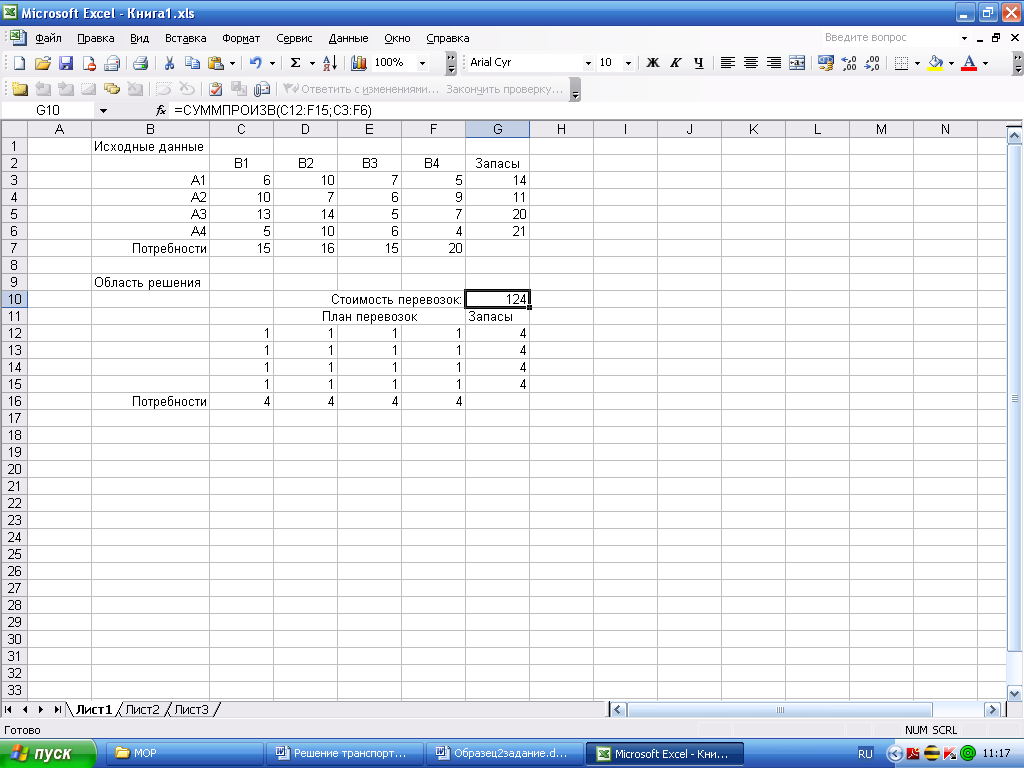
Далее выполняют команду Поиск решения (вкладка Сервис или Данные).
Установить целевую ячейку G10, равной минимальному значению.
В поле ввода Изменяя ячейки установить C12:F15
В поле ввода Ограничения установить C12:F15 >= 0
C16:E16 = C7:E7
G12:G15 = G3:G6
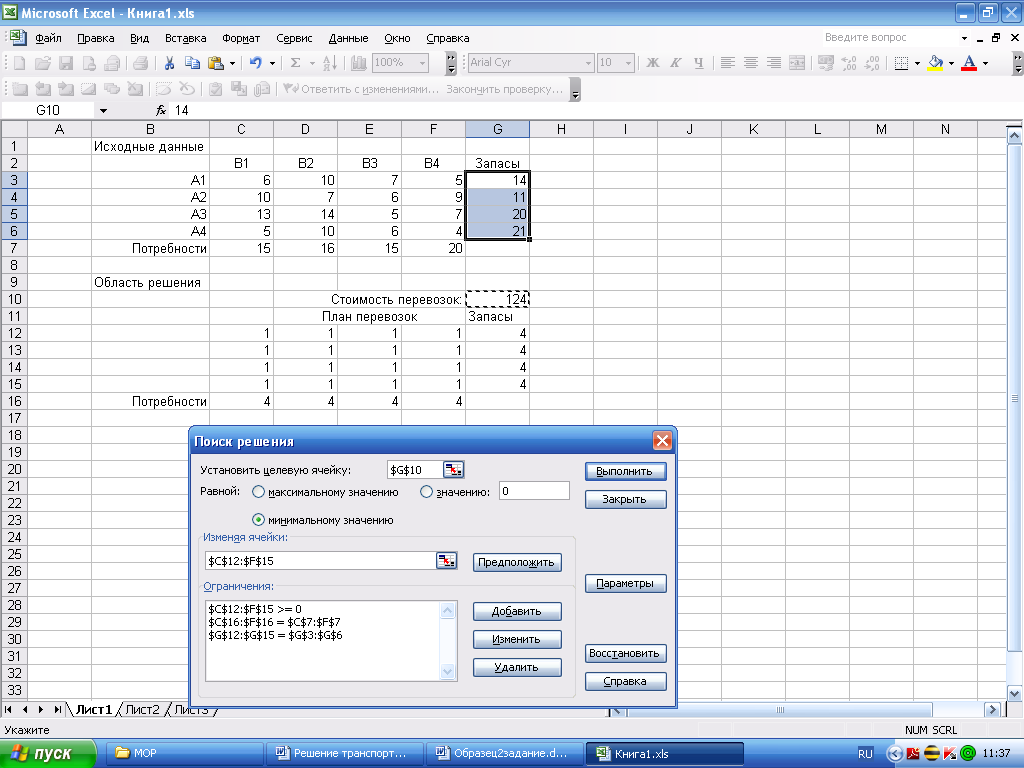
Далее нажимают на кнопку Параметры .
Вычисления производятся при нажатии кнопки Выполнить два раза. Получим решение задачи:
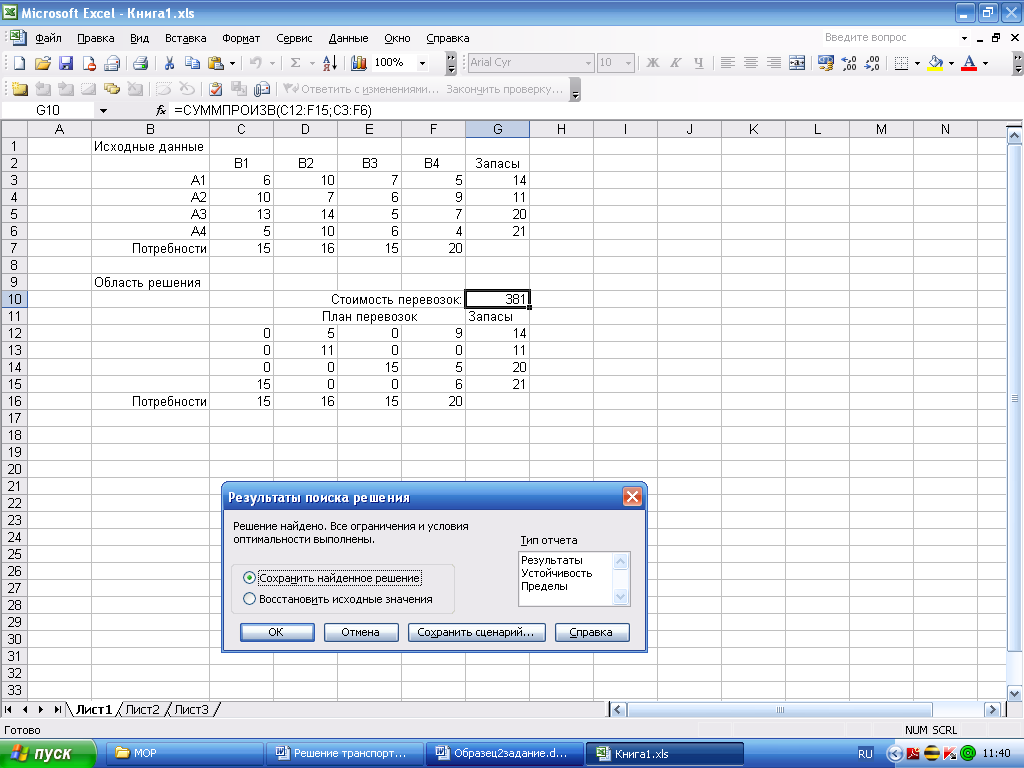
3.2.3. Обоснование распределения финансовых ресурсов между проектами.
На развитие трех предприятий выделено В млн. руб. Известна эффективность капитальных вложений xi в каждое j-е предприятие, заданная таблично значением нелинейной функции fj(xi), где
, 
14 = u1 + v4 c14 = 0 + 5 – 5 = 0,
21 = u2 + v1 c21 = – 3 + 6 – 10 = –7 < 0,
23 = u2 + v3 c23 = – 3 + 1 – 6 = –8 < 0,
24 = u2 + v4 c24 = – 3 + 5 – 9 = –7 < 0,
31 = u3 + v1 c31 = 4 + 6 – 13 = –3 < 0,
34 = u3 + v4 c34 = 4 + 5 – 7 = 2 > 0,
42 = u4 + v2 c42 = – 1 + 10 – 10 = –1 < 0,
43 = u4 + v3 c43 = – 1 + 1 – 6 = –6 < 0.
Результаты расчета представлены в распределительной таблице:
| bj ai | 1 | 2 | 3 | 4 | ui | |
| 15 | 16 | 15 | 20 | |||
| 1 | 14 | 6 14 | 10 | 7 (–6) | 5 (0) | 0 |
| 2 | 11 | 10 (–7) | 7 11 | 6 (–8) | 9 (–7) | –3 |
| 3 | 20 | 13 (–3) | 14 5 | 5 15 | 7 (2) | 4 |
| 4 | 21 | 5 1 | 10 (–1) | 6 (–6) | 4 20 | 1 |
| vj | 6 | 10 | 1 | 5 | | |
Клетка (3, 4) имеет положительную оценку 34 = 2 > 0, следовательно, решение Х1 не оптимальное, а для клетки строим новый цикл: 0*5
141200* (все вершины цикла, кроме первой, находятся в занятых клетках, углы прямые, число вершин четное). У вершин цикла с соответствующими значениями поставок по правилу чередования знаков ставим знаки (+) и (–), начиная со свободной клетки. У вершин со знаком (–) выбираем минимальный груз = min[14, 20, 5] = 5.
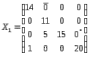
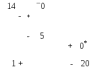
Его прибавляем к грузам, стоящим у положительных вершин, и отнимаем от грузов, стоящих у отрицательных вершин. Получаем новый цикл:
Получили новое решение задачи (план перевозок):
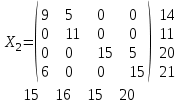
Справа и внизу матрицы проведена проверка: исходные данные запасов и потребностей в результате перераспределения поставок не изменились.
Значение целевой функции:
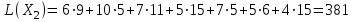(ед.). Значение целевой функции уменьшилось на 10 ед.
Проверка решения Х2 на оптимальность. Расчет потенциалов для занятых клеток: u1 = 0;
клетка (1, 1): v1 = c11 – u1 = 6 – 0 = 6;
клетка (4, 1): u4 = c41 – v1 = 5 – 6 = 1;
клетка (1, 2): v2 = c12 – u1 = 10 – 0 = 10;
клетка (2, 2): u2 = c22 – v2 = 7 – 10 = 3;
клетка (4, 4): v4 = c44 – u4 = 4 – (1) = 5;
клетка (3, 4): u3 = c34 – v4 = 7 – 5 = 2;
клетка (3, 3): v3 = c33 – u3 = 5 – 2 = 3;
Расчет оценок свободных клеток:
13 = u1 + v3 c13 = 0 + 3 – 7 = –4 < 0,
14 = u1 + v4 c14 = 0 + 5 – 5 = 0,
21 = u2 + v1 c21 = – 3 + 6 – 10 = –7 < 0,
23 = u2 + v3 c23 = – 3 + 3 – 6 = –6 < 0,
24 = u2 + v4 c24 = – 3 + 5 – 9 = –7 < 0,
31 = u3 + v1 c31 = 2 + 6 – 13 = –5 < 0,
32 = u3 + v2 c32 = 2 + 10 – 14 = –2 < 0,
42 = u4 + v2 c42 = – 1 + 10 – 10 = –1 < 0,
43 = u4 + v3 c43 = – 1 + 3 – 6 = –4 < 0.
Результаты расчета представлены в распределительной таблице:
| bj ai | 1 | 2 | 3 | 4 | ui | |
| 15 | 16 | 15 | 20 | |||
| 1 | 14 | 6 9 | 10 5 | 7 (–4) | 5 (0) | 0 |
| 2 | 11 | 10 (–7) | 7 11 | 6 (–6) | 9 (–7) | –3 |
| 3 | 20 | 13 (–5) | 14 (–2) | 5 15 | 7 5 | 2 |
| 4 | 21 | 5 6 | 10 (–1) | 6 (–4) | 4 15 | 1 |
| vj | 6 | 10 | 3 | 5 | | |
Все оценки свободных клеток положительные, следовательно, решение Х2 оптимально.
Оценка клетки (1, 4) 14 = 0 означает, что задача имеет альтернативные решения.
Методика нахождения альтернативного решения
Для нахождения альтернативного решения для клетки с нулевой оценкой строят еще один цикл перераспределения поставок по тем же правилам, что и при улучшении решения. Проверка оптимальности решения для альтернативного решения не производится. Следует проверить значение целевой функции, соответствующее альтернативному решению: оно должно совпадать со значением целевой функции, соответствующим первому оптимальному решению.
Найдем одно из альтернативных решений. Для этого для клетки с нулевой оценкой строим еще один цикл: 0*96150* (все вершины цикла, кроме первой, находятся в занятых клетках, углы прямые, число вершин четное). У вершин цикла с соответствующими значениями поставок по правилу чередования знаков ставим знаки (+) и (–), начиная со свободной клетки. У вершин со знаком (–) выбираем минимальный груз = min[9, 15] = 9.
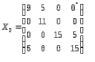
Его прибавляем к грузам, стоящим у положительных вершин, и отнимаем от грузов, стоящих у отрицательных вершин. Получаем новый цикл:
Получили альтернативное решение задачи (план перевозок):
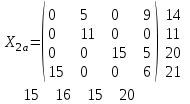
Значение целевой функции:
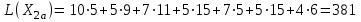(ед.).Значение целевой функции альтернативного решения совпало со значением целевой функции первого оптимального решения транспортной задачи.
Таким образом, решение транспортной задачи:
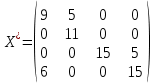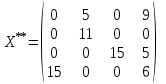, , L(X*) = 381(ед.).5. Решение транспортной задачи в среде Microsoft Exсel
Ввод исходных данных (в области C3:F6 – тарифы на перевозку продукции; в столбце G3:G6 – запасы; в ячейках С7
, D7, E7, F7 – потребности).
В области решения в ячейке G10 введите формулу стоимости перевозок:
=СУММПРОИЗВ(C12:F15;C3:F6). Для этого необходимо нажать на значок f(x) на панели инструментов, выбрать математическую функцию СУММПРОИЗВ и ввести два массива C12:F15 и C3:F6. Далее в области C12:F15 проставьте любое первоначальное решение (например, единицы)/
В ячейке С16 записывается формула: =СУММ(C12:C14), т.е. сумма значений по столбцу (можно выделить значения столбца и нажать на знак автосуммы Σ на панели инструментов). Аналогично в D16, E16, F16. Автоматически суммируются значения по столбцам.
В ячейке G12 записывается формула: =СУММ(C12:F12), т.е. сумма значений по строке (можно выделить значения строки и нажать на знак автосуммы Σ на панели инструментов). Аналогично в G13, G14, G15. Автоматически суммируются значения по строкам:
Далее выполняют команду Поиск решения (вкладка Сервис или Данные).
Установить целевую ячейку G10, равной минимальному значению.
В поле ввода Изменяя ячейки установить C12:F15
В поле ввода Ограничения установить C12:F15 >= 0
C16:E16 = C7:E7
G12:G15 = G3:G6
Далее нажимают на кнопку Параметры .
Вычисления производятся при нажатии кнопки Выполнить два раза. Получим решение задачи:
3.2.3. Обоснование распределения финансовых ресурсов между проектами.
На развитие трех предприятий выделено В млн. руб. Известна эффективность капитальных вложений xi в каждое j-е предприятие, заданная таблично значением нелинейной функции fj(xi), где
,