ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 179
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПАРАМЕТРЛІ ЕСЕПТЕРДІ ШЕШУДІҢ ӘДІС-ТӘСІЛДЕРІ
Әдістемелі құралында қарапайым математиканың ең қиын тақырыптарының бірі – "параметрлері бар есептер"қарастырылады. Параметрлері бар әр түрлі есептер (теңдеулер, теңсіздіктер, теңдеулер мен теңсіздіктер жүйесі және т.б.) және оларды шешу әдістері келтірілген.
Әдістемелік құралы математика мұғалімдері мен жалпы білім беретін мектептердің, лицейлердің, гимназиялардың оқушыларына, сондай - ақ педагогикалық жоғары оқу орындарының Математика мамандықтарының студенттері мен оқытушыларына пайдалы болады.
Әдістемелік құралы математика пәнінен емтиханға дайындалуға көмектеседі және математикалық бейіні бар сыныптар мен мектептер үшін тиісті тақырып бойынша элективті курстың негізі болады.
-
МАЗМҰНЫ
І. Кіріспе
ІІ. Негізгі бөлім
2.1. Параметрлері бар теңдеулерді, теңсіздіктерді, жүйелерді шешу.
2.2. Параметрлері бар есептерді шешудің координаталық-параметрлік әдісі
2.3. Параметрлі интервалдар әдісімен бөлшек-рационалды теңсіздіктерді шешу
2.4. Көрсеткіштік, логарифмдік және тригонометриялық функциялардың қасиеттеріне байланысты параметрлері бар теңдеулерді шешу
ІІІ. Қорытынды
ІҮ. Пайдаланылған әдебиеттер.
-
І. КІРІСПЕ
Параметрлері бар есептер оқушылардың логикалық ойлауы мен математикалық мәдениетін қалыптастыруда маңызды рөл атқарады, бірақ оларды шешу оларға айтарлықтай қиындықтар тудырады. Себебі параметрлері бар әрбір теңдеу әрқайсысы үшін шешім алынуы керек кәдімгі теңдеулердің тұтас класы болып табылады. Мұндай міндеттер бірыңғай мемлекеттік емтиханда және жоғары оқу орындарына түсу емтихандарында ұсынылады.
Егер теңдеуде кейбір коэффициенттер нақты сандық мәндермен берілмесе, бірақ әріптермен көрсетілсе, онда олар параметрлер деп аталады, ал теңдеу параметрлік болады.Параметрлері бар есептерде белгісіз шамалармен бірге сандық мәндері нақты көрсетілмегенімен, белгілі және белгілі бір сандық жиында берілген деп саналатын шамалар пайда болады. Кезінде бұл есептің шартына кіретін параметрлер шешімнің логикалық және техникалық бағытына және жауап формасына айтарлықтай әсер етеді.
Параметрлері бар тапсырмалар өте алуан түрлі. Оларды шешудің жалпы әдістері жоқ (тек сызықтық теңдеулерді, теңдеулерді және параметрі бар теңдеулер жүйесін, квадрат теңдеулерді және квадрат триномияның түбірлерінің берілген сандарға қатысты орналасуына байланысты есептерді қоспағанда). Барлық есептерді параметрлермен біріктіретін жалғыз нәрсе-олардың кез-келгенін келесі екі топтың біріне жатқызуға болады: параметрдің барлық мәндерін табу қажет болатын есептер, олардың әрқайсысында белгілі бір шарт орындалады (теңсіздіктің шешімі бар, теңдеудің түбірлері берілген аралыққа жатады және т. б.) және есептер, онда параметрлермен теңдеуді (теңсіздік, жүйе) шешу қажет. Келесі жағдайда, мәселенің қандай параметр мәндерінде шешімдері бар екенін анықтау керек және осы шешімдерді параметр мәндерінің әрқайсысы үшін көрсету керек (егер кейбір параметр мәндерінде шешімдер болмаса, онда жауапта дәл осылай жазу керек-әйтпесе шешім толық емес деп саналуы мүмкін).
Көптеген есептерді параметрлермен шешу қандай да бір жолмен сызықтық және квадраттық функциялардың қасиеттерімен байланысты. а параметрі бар кез келген сызықтық теңдеу түрге әкелуі мүмкін
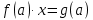 .
.Егер
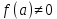 -ге тең болса, теңдеудің жалғыз шешімі болады.
-ге тең болса, теңдеудің жалғыз шешімі болады.Параметрлері бар есептер толыққанды математикалық іс-әрекеттің кең өрісін білдіреді. Бұл мәселелерді шешу студенттерге жалпы сипаттағы эвристикалық әдістердің едәуір санын ашады, тұлғаның математикалық дамуы үшін құнды.
Параметрлері бар тапсырмалар диагностикалық және болжамды мәнге ие. Олар мектеп математикасының негізгі бөлімдерін, математикалық және логикалық ойлау деңгейін, зерттеу қызметінің бастапқы дағдыларын тексеруге мүмкіндік береді. Тәжірибе көрсеткендей, параметрлері бар есептерді шешу әдістерін меңгерген студенттер басқа тапсырмаларды сәтті орындайды. Әрине, параметрлері бар есептерді шешу математикалық ойлауды қалыптастырудың қуатты құралдарының бірі болып табылады:
- ақыл-ой операцияларын дамыту (салыстыру, ұқсастық, жіктеу, нақтылау, жалпылау) және талдау мен синтездеу қабілетін дамыту үшін үлкен әлеуетті мүмкіндіктерге ие;
- кем дегенде екі баламаны қарастырумен байланысты кез-келген тапсырмаға тән логикалық пайымдау мәдениетін қалыптастырады, ал параметрлік есептерді шешудің логикалық құрылымы, әдетте, әлдеқайда көп;
– ойлау икемділігін дамытады, ол әдеттегі әрекет ету тәсілінен тыс жүру қабілетімен сипатталады (өйткені пара - метрикалық теңдеулерді, теңсіздіктер мен жүйелерді шешкен кезде параметр тең айнымалы ретінде әрекет ете алады) және т. б.;
– теңдеулерді, теңсіздіктерді немесе олардың жүйелерін шешудің әртүрлі тәсілдерін зерттеу, шешудің ұтымды жолдарын іздеуге ұмтылу (көптеген теңдеулер мен параметрлері бар теңсіздіктер шешудің сапалы тәсілдеріне мүмкіндік береді)сипатталатын ойлаудың фокусы мен белсенділігін қалыптастырады;
- объектілер немесе олардың қасиеттері арасындағы қатынастардың динамикасын қолдану, айнымалылар мен олардың өзгерістерін көру қабілетімен сипатталатын "функционалды ойлауды" қалыптастырыңыз;
– визуалды ойлаудың қалыптасуына ықпал етеді (өйткені параметрлік теңдеулерді, теңсіздіктерді және олардың жүйелерін талдаудың және шешудің әртүрлі графикалық әдістері бар).
Әдістемелік құралында параметрлері бар есептердің әртүрлі түрлері келтірілген, оларды шешудің әртүрлі әдістері көрсетілген. Бұл нұсқаулықтың негізгі мақсаты-қарапайым математика аясында оқырманның математикалық мәдениетін арттыру.
-
2.1. ПАРАМЕТРЛЕРІ БАР ТЕҢДЕУЛЕРДІ, ТЕҢСІЗДІКТЕРДІ, ЖҮЙЕЛЕРДІ ШЕШУ.
Математика бағдарламасында мамандандырылмаған математикалық мектептер үшін параметрлері бар есептерге шамалы ме - жүз берілетіні белгілі. Сондықтан, ең алдымен, параметр идеясы бар жалпы білім беретін математиканың бөлімдерін көрсетейік.
Сонымен, кейбір ұғымдарды енгізу кезінде оқушылар параметрлермен кездеседі. Егжей-тегжейлі анықтамаларды бермей, мысал ретінде келесі нысандарды қарастырыңыз:
-
функция тікелей пропорционалдылық: у = кх; -
сызықтық функция: y = x + b; -
сызықтық теңдеу: ах + b = 0; -
бірінші дәрежелі теңдеу: ах + b = 0; -
Квадрат теңдеу: ах2 + bх + с = 0.
Мектеп курсында қарастырылған параметрлері бар есептерге, мысалы, сызықтық және квадрат теңдеулердің шешімдерін жалпы түрде іздеу, параметрлердің мәндеріне байланысты олардың тамырларының санын зерттеу жатады.
Оқырман ең бастысы үйренуі керек: параметр тұрақты, бірақ белгісіз сан болғандықтан, қосарланған сипатқа ие. Біріншіден, болжамды атақ параметрмен сандық сынық ретінде "байланысуға" мүмкіндік береді, екіншіден, қарым - қатынас еркіндігінің дәрежесі оның белгісіздігімен шектеледі.
Параметрмен алғаш танысқан кезде үйренуге болатын негізгі нәрсе - егер сіз қаласаңыз да, тіркелген, бірақ белгісіз санмен мұқият жұмыс істеу қажеттілігі.
Параметр - мәндері белгілі бір жиынтықтың элементтерін бір-бірінен ажыратуға қызмет ететін шама. Мысалы, декарттық тікбұрышты координаттарда (х - a)2 + (у – b)2 = 1 теңдеуі хОу жазықтығындағы 1 радиус шеңберлерінің жиынын анықтайды.
аx2 + bx + c = 0 теңдеуін қарастырайық. Әрине, теңдеуде біз кейбір әріптерді белгісіз деп санаймыз, ал басқа параметрлер негізінен шартты болып табылады. Нақты тәжірибеде айнымалылар арасындағы бірдей қатынастан кейбір айнымалыларды басқалар арқылы білдіруге тура келеді, яғни теңдеуді бір әріпке қатысты шешіп, оны белгісіздің белгісі, ал басқа әріптерді параметрлер деп санаңыз.
Дәстүр бойынша белгісіздер латын алфавитінің соңғы әріптерімен белгіленеді - х, у, z, ал параметрлер бірінші – а, в, басқа алфавиттің әріптерімен немесе жалпы әріптерімен (мысалы, грек).
Есепті параметрлермен шешу дегеніміз-тапсырманың шешімдері бар параметрлердің барлығын және тек білімдерін табу.
Параметрлер нақты мәндерді қабылдайды және параметрлері бар есептерде нақты сандар ізделеді деп келісілді.
"Параметр" ұғымына әртүрлі анықтамалар беріледі. Мысалы, С.И.Новоселовтың "алгебраның арнайы курсы" кітабында келтірілген анықтаманы қарастырайық, ол келесі басылымдардың көпшілігінің анықтамаларына негіз болды: "егер белгісіз теңдеуге әріптермен көрсетілген сандар кірсе, онда олар параметрлер деп аталады". Әріптің белгіленуі "параметр"сияқты ұғымның маңызды белгісі емес екені анық.
Теңдеуді қарастырайық
(a, b, c, …, k, x)=(a, b, c, …, k, x), (1)
мұндағы a, b, c, ..., k, x-айнымалы шамалар.
Айнымалы мәндердің кез келген жүйесі
а = а0, b = b0, c = c0, …, k = k0, x = x0,
осы теңдеудің сол және оң жақтары нақты мәндерді қабылдайтын кезде a, b, c, ..., k, x айнымалыларының рұқсат етілген мәндер жүйесі деп аталады.А барлық рұқсат етілген мәндердің жиыны болсын а, B-барлық рұқсат етілген мәндердің жиыны b, т. б., Х – барлық рұқсат етілген мәндердің жиыны х, яғни, А шегі а, b шегі B,..., x шегі x. Егер A, B, C, ..., K жиындарының әрқайсысында сәйкесінше a, b, c, ..., K бір мәнін таңдап, бекітіп, оларды (1) теңдеуге ауыстырсақ, онда біз X-ге қатысты теңдеу аламыз, яғни бір белгісіз теңдеу. Теңдеуді шешкен кезде тұрақты деп саналатын а, b, c, ..., k айнымалылары параметрлер деп аталады, ал теңдеудің өзі параметрлері бар теңдеу деп аталады.
Параметрлер латын алфавитінің бірінші әріптерімен белгіленеді: a, b, с, d,..., k, l, m, n және белгісіз – x,y, z әріптерімен.
Параметрлері бар теңдеуді шешу дегеніміз-параметрлердің қандай мәндерінде шешімдер бар екенін және олардың не екенін көрсету.
Бірдей параметрлері бар екі теңдеу эквивалентті деп аталады, егер:
а) олар бірдей параметр мәндерімен мағынасы бар;
б) бірінші теңдеудің әрбір шешімі екіншісінің шешімі болып табылады және керісінше.
Шешім алгоритмі. Біз теңдеудің анықтау аймағын табамыз.
ХОА координаттар жүйесінде а=(х) функцияның графигін құрамыз.
а = с түзудің а=(х) функциясының графигімен қиылысу нүктелерін табамыз, мұндағы с(-;+.) Егер а=с түзу болса, а=(х) графикті қиып өтеді, онда біз қиылысу нүктелерінің абсциссаларын анықтаймыз. Ол үшін а=(х) теңдеуді х жиынына қатысты шешу жеткілікті.
Жауапты жазамыз.
І.Теңдеуді шеш
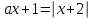 (1)
(1)Шешімі.
Х=0 теңдеудің түбірі болмағандықтан, а-ға қатысты теңдеуді шешуге болады:
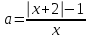 немесе
немесе 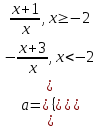
Функция графигі-екі " желімделген " гипербола. Бастапқы теңдеудің шешімдерінің саны сызылған сызық пен түзудің қиылысу нүктелерінің санымен анықталады у=а.
Егер а (-;-1](1;+)
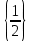 , онда түзу у=а (1) теңдеуінің графигін бір нүктеде қиып өтеді. Теңдеуді шешкен кезде осы нүктенің абсциссасын табамыз
, онда түзу у=а (1) теңдеуінің графигін бір нүктеде қиып өтеді. Теңдеуді шешкен кезде осы нүктенің абсциссасын табамыз 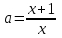 , х- ке қатысты.
, х- ке қатысты.Осылайша, осы аралықта (1) теңдеудің шешімі болады
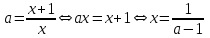 .
.Егер а
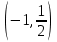 , онда у=а түзуі (1) теңдеуінің графигін екі нүктеде қиып өтеді. Бұл нүктелердің абсциссаларын
, онда у=а түзуі (1) теңдеуінің графигін екі нүктеде қиып өтеді. Бұл нүктелердің абсциссаларын 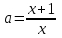 және
және 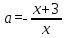 теңдеулерден табуға болады, бұдан шығатыны
теңдеулерден табуға болады, бұдан шығатыны 
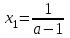 және
және 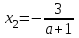 .
.Егер а
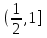 , онда у=а түзуі (1) теңдеу графигін қиып өтпейді, сондықтан шешімдер жоқ.
, онда у=а түзуі (1) теңдеу графигін қиып өтпейді, сондықтан шешімдер жоқ.Жауап:
Егер а (-;-1](1;+)
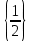 , онда
, онда 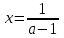 ;
;Егер а
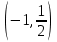 , онда
, онда 
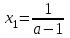 ,
, 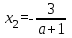 ;
;Егер а