Файл: Параметрлі есептерді шешуді дістсілдері.docx

Енді (3)жүйені қарастыруға жүгінейік. Бұл жүйенің бірінші теңдеуі хОу жазықтығында бірінші және екінші квадранттарда орналасқан гиперболалар тобын анықтайды. Жүйенің екінші (3) теңдеуі хОу жазықтығында түзулер тобын анықтайды.

Бекітілген оң a және b жүйеде (3) екі, үш немесе төрт шешім болуы мүмкін. Шешімдердің саны теңдеу арқылы берілген түзудің болуына байланысты 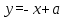, 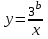гиперболамен ортақ нүктелер бар 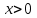болғанда, ( 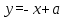түзуі әрқашан 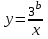функция графигімен бір қиылысу нүктесі болады).

Мұны шешу үшін теңдеуді қарастырыңыз

,

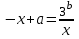бұл келесі түрде қайта жазуға ыңғайлы



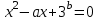
Енді есептің шешімі соңғы теңдеудің D дискриминантын қарастыруға дейін азаяды:

• 
  Егер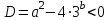 , т.е. если 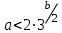, то система (3) имеет два решения;
  
• 
  если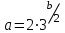 , онда (3) жүйенің үш шешімі бар;
  
• 
  егер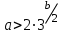 , онда (3) жүйе төрт шешімге ие.
  

Осылайша, (1) және (2) жүйелердегі шешімдердің бірдей саны төрт. Және 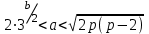болады.

Жауап:

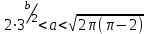
Параметрлермен теңсіздіктер. Негізгі анықтамалар.

Теңсіздік

(a, b, c, …, k, x)>(a, b, c, …, k, x), (1)

мұнда a, b, c, …, k – параметрлер, ал x – нақты айнымалы шама, параметрлері бар бір белгісіз теңсіздік деп аталады.

Параметр мәндерінің кез келген жүйесі а = а₀, b = b₀

---

, c = c₀, …, k = k₀, кейбір функциямен

(a, b, c, …, k, x) және

(a, b, c, …, k, x

нақты сандар аймағында мағынасы бар, параметрлердің рұқсат етілген мәндер жүйесі деп аталады.

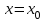рұқсат етілген x мәні деп аталады, егер

(a, b, c, …, k, x) және

(a, b, c, …, k, x

параметр мәндерінің кез келген рұқсат етілген жүйесі үшін жарамды мәндерді қабылдаңыз.

Барлық рұқсат етілген х мәндерінің жиынтығы теңсіздікті анықтау аймағы деп аталады (1).

Нақты сан х₀ теңсіздіктің жеке шешімі деп аталады (1), Егер теңсіздік болса (a, b, c, …, k, x₀)>(a, b, c, …, k, x₀)

кез-келген рұқсат етілген параметрлер жүйесінде дұрыс.

Теңсіздіктің барлық жеке шешімдерінің жиынтығы (1) осы теңсіздіктің жалпы шешімі деп аталады.

Теңсіздікті шешу (1) дегеніміз-параметрлердің қандай мәндерінде жалпы шешім бар екенін және оның қандай екенін көрсету.

Екі теңсіздік

(a, b, c, …, k, x)>(a, b, c, …, k, x) және (1)

(a, b, c, …, k, x)>(a, b, c, …, k, x) (2)

егер олар бірдей параметрлер мәндерінің жүйелерінің бірдей жиынтығында бірдей ортақ шешімдерге ие болса, эквивалентті деп аталады.

---

Шешім алгоритмі.

• 
  Біз осы теңсіздікті анықтау аймағын табамыз.
  
• 
  Теңсіздікті теңдеуге дейін азайтайық.
  
• 
  Біз а-ны х-тен функция ретінде білдіреміз.
  
• 
  ХОа координаттар жүйесінде берілген теңсіздікті анықтау аймағына кіретін х мәндері үшін а = (х) функцияларының графиктерін құрамыз.
  
• 
  Біз осы теңсіздікті қанағаттандыратын көптеген нүктелерді табамыз.
  
• 
  Параметрдің нәтижеге әсерін зерттейміз.
  
• 
  графиктердің қиылысу нүктелерінің абсциссаларын табыңыз.
  
• 
  а=соnst түзуін жазамыз және оны --тен +-ке дейін созамыз.
  
• 
  Жауапты жазамыз.
  

Бұл ХОа координаттар жүйесін қолдана отырып, параметрлермен теңсіздіктерді шешудің алгоритмдерінің бірі ғана. Стандартты ХОУ координаттар жүйесін қолдана отырып, шешудің басқа әдістері де мүмкін.

Мысал. І. а параметрінің барлық рұқсат етілген мәндері үшін теңсіздікті шешіңіз



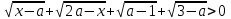
Шешімі.

Теңсіздіктер жүйесімен анықталған а параметрін анықтау саласында



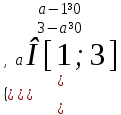
бұл теңсіздік теңсіздіктер жүйесіне тең



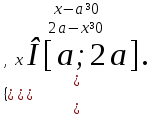
Егер 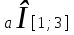, бастапқы теңсіздіктің шешімдері сегментті толтырады .

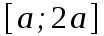Жауап: , .
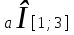II. Теңсіздікті шешіңіз 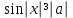на 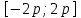а параметр мәндеріне байланысты.

Шешімі.

1. 
   Біз рұқсат етілген мәндер аймағын табамыз –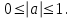
   
2. 
   хОу координаттар жүйесінде функцияның графигін құрайық.
   

• 
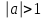  болғанда, шешімдердің теңсіздігі жоқ.
  
• 
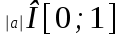  болғанда, 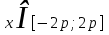үшін шешім x арақатынасын қанағаттандырады 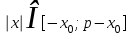, мұндаға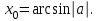
  

---

Жауап: теңсіздіктің шешімдері

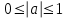
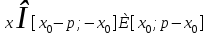, мұндаға 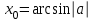, 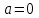болғанда, шешімі 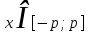; 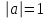болғанда, шешімі .

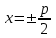IІІ. Теңсіздікті шешіңіз


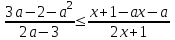
Шешімі.

Рұқсат етілген мәндер аймағы немесе асимптота сызықтарын табамыз

1. 
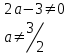
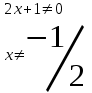
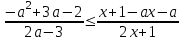
   Біз графиктерді полярлық координаттар жүйесінде салу керек функциялардың теңдеулерін табамыз; ол үшін теңдікке көшейік:
   

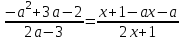
Алымды көбейткіштерге бөлейік.



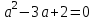
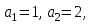болғандықтан, онда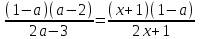



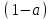теңдіктің екі бөлігін де бөлейік 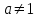_{болғанда}. Онда 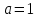шешім болып табылады: теңдеудің сол жағы оң жақ бөлікке тең және нөлге тең .







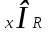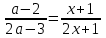
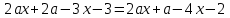
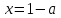
3. Полярлық координаттар жүйесінде ХОa-да функциялардың графиктерін құру

---

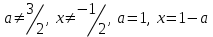
біз қалыптасқан аймақтарды нөмірлейміз (осьтер рөл атқармайды). Тоғыз аймақ шықты.

4. Біз осы теңсіздікке қай аймақ сәйкес келетінін іздейміз, ол үшін біз аймақтан нүкте алып, теңсіздікке ауыстырамыз.

Түсінікті болу үшін кесте құрайық.

№	нүкте	теңсіздік:	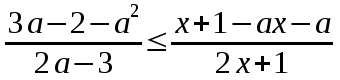шешім
1			-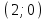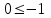
2			+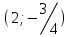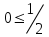
3			-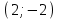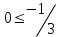
4			+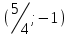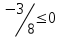
5			-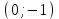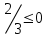
6			+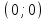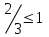
7			-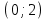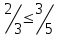
8			+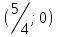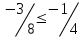
9			-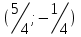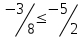

---