ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 181
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
)(X- )(X-
)(X- )(X-
)(X- )<0 x интервалдары үшін, (
)<0 x интервалдары үшін, ( ;
; ), (
), ( ;
; ),
),
Ескерту 1.
Сандардың өзі ( ;
; ),(
),( ;
; ) теңсіздіктің шешімі емес.
) теңсіздіктің шешімі емес.
(X- )(X-
)(X- )(X-
)(X- )(X-
)(X- )>0
)>0
Ескерту 2.
Түр теңсіздіктерінің көптеген шешімдері A(x)≥0 және A(x)≤0 және мұнда,
A(x)=(X- ) (X-
) (X- )∙…∙(X-
)∙…∙(X- );
);
барлық шешімдердің жиынтығы бар n ≥ 1,n∈N теңсіздіктер A(x)>0 және A(x)<0 және теңдеудің барлық шешімдерінің жиынтығы A(x)=0
Ескерту 4. Егер теңсіздік канондық түрге әкелсе, онда оң жақта"+"белгісі болады.
Ескерту 5. Теңсіздік белгісі "қатаң емес": көпмүшенің немесе нумератордың сандық түзу түбірінде - боялған шеңберлер. "Қатаң" және "қатаң емес" теңсіздіктер үшін бөлгіштің тамыры "бос" .
Бөлшек-рационалды теңсіздіктер.
Анықтама. Бөлшек рационалды түрдің теңсіздігі деп аталады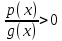 , мұнда p(x) және g(x) - көпмүшелер.
, мұнда p(x) және g(x) - көпмүшелер.
Рационалды теңсіздіктерден айырмашылығы, бөлшек рационалдылар айнымалының барлық мәндері үшін анықталмауы мүмкін. Атап айтқанда, мұндай мәндерді қарастырудан алып тастау керек х, онда көпмүше g(x) ол нөлге айналады (өйткені оны нөлге бөлуге болмайды!).
Егер екінші жағынан, барлық рұқсат етілген мәндерде бөлшек рационалды өрнек бар екені анық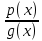
және p(x)*g(x) көбейтіндісінің көпмүшесі бірдей белгіге ие.интервал математический дробный неравенство
2. Шешім алгоритмі
Бөлшек-рационалды теңсіздіктерді шешудің мысалдарын қарастырыңыз.
Мысал 1. Теңсіздікті шешіңіз
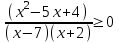 .
.
Шешім. 1. Алдымен біз теңсіздіктің рұқсат етілген мәндерінің аймағын табамыз (бұдан әрі қысқартылған түрде жазамыз - рұқсат етілген мәндер аймағы). Әлбетте, бұл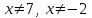 .
.
2. Бөлшек-рационалды теңсіздікті рационалдыға айналдырайық:
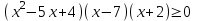 .
.
3. Алынған теңсіздіктің сол жағын көбейтейік:
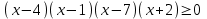 .
.
4. Көпмүшенің түбірлері -2, 1, 4 және 7 сандарының "бірлік" еселігі бар екенін ескеріңіз, оларды сандық оське қойып, алынған аралықтарда теңсіздік белгілерін орналастырыңыз:
5. Біз нақты жауапты жазамыз, оның ішінде алымда тұрған көпмүшенің тамыры және бөлгіштің түбірлерін қоспағанда.
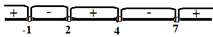
Сурет 20
Жауап: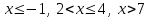 .
.
Назар аударыңыз! Жауапты жазу үшін теңсіздіктерді де, бос орындарды да пайдалануға болады. Мысалы, бұл жауапты келесі түрде де жазуға болады:
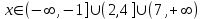 .
.
Келесі мысалда біз бірнеше түбірлік теңсіздіктерді қарастырамыз. Мысал 2. Теңсіздікті шешіңіз: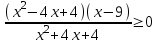 .
.
Шешім. Алдымен алымдағы бірінші өрнек пен бөлгіштегі өрнек толық квадраттар екенін ескеріңіз. Келесі: бөлгіш нөлге айналады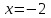 , сондықтан рұқсат етілген мәндер аймағы:
, сондықтан рұқсат етілген мәндер аймағы: 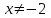 .
.
Рационалды теңсіздікке көшейік, аламыз: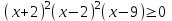 .
.
Алынған теңсіздіктің сол жағындағы көпмүшенің тамырларын сандық оське қойып, осы көпмүшенің белгілерін алынған аралықтарда анықтаймыз. -2 және 2 тамырларының еселігін ескере отырып, біз аламыз:
Назар аударыңыз, белгі тек 9-да өзгереді, ал 2 және -2-де ол сақталады, өйткені бұл жұп еселіктің түбірлері.

Сурет 21
Енді жауапты" жинайық": негізгі аралыққа-сәуле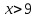 2 және 9 алымдарының түбірлерін қосыңыз, ал бөлгіштің түбірі -2 алынып тасталады. Жауап:
2 және 9 алымдарының түбірлерін қосыңыз, ал бөлгіштің түбірі -2 алынып тасталады. Жауап:
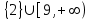 .
.
Тағы бір маңызды мысалды қарастырайық, өйткені дәл осындай тапсырмаларда талапкерлер көптеген қателіктер жібереді.
Мысал 3. Теңсіздікті шешіңіз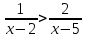 .
.
Шешім. Бұл теңсіздік канондық бөлшек рационалға ұқсамайды, бірақ ол төмендейді. Ең бастысы-оны дұрыс жасау. Мұны істеу үшін біз бөлшекті теңсіздіктің оң жағынан солға ауыстырамыз және алынған екі бөлшек айырмашылығын ортақ бөлгішке келтіреміз: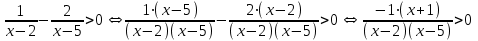 .
.
Алымды -1-ге қысқартайық, ал теңсіздік белгісі керісінше өзгереді: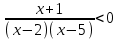 . Енді біздің алдымызда түпнұсқаға тең канондық бөлшек-рационалды теңсіздік тұр. Біз оны интервал әдісімен шешеміз. Жауап:
. Енді біздің алдымызда түпнұсқаға тең канондық бөлшек-рационалды теңсіздік тұр. Біз оны интервал әдісімен шешеміз. Жауап: 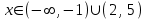 .
.
Ескерту. Көбінесе мұндай есептер дұрыс шешілмейді, атап айтқанда: сол жақ бөліктің нумераторын оң жақ бөлгішке көбейту және керісінше. Нәтижесінде мүлдем басқа теңсіздік пайда болады: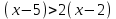 , бұл сызықтық теңсіздікке дейін азаяды
, бұл сызықтық теңсіздікке дейін азаяды 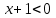 ол үшін жауап:
ол үшін жауап: 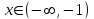 тек ішінара дұрыс сәйкес келеді.
тек ішінара дұрыс сәйкес келеді.
Мысал 4.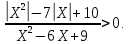
Шешім.Біз теңсіздікті интервал әдісімен шешеміз.Функциялардың нөлдерін табыңыз f(x)=x, модуль белгісімен тұрған: x=0.
1.Егер x≤0, онда теңсіздік форманы алады
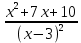 >0,
>0,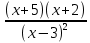 >0.
>0.
x∈(-∞;-5)∪(-2;0].
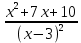 >0,
>0,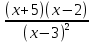 >0
>0
x∈(0;2)∪(5;+∞).
Бастапқы теңсіздіктің шешімі бірінші және екінші жағдайларда алынған шешімдердің жиынтығы болып табылады:
x∈(-∞;-5)∪(-2;2)∪(5;+∞).
Жауап: х∈(-∞;-5)∪(-2;2)∪(5;+∞).
Мысал5: Бөлшек рационалды теңсіздікті шешіңіз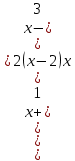 >0
>0
Шешім.х=5,x=-1,x=0,x=2,x=3 сандық түзу нүктесінде белгілеп, теңсіздіктің сол жағындағы белгілердің өзгеруін зерттейміз.Теңсіздікті шешу интервалдарды біріктіру болып табылады: (-5;-1)∪(-1;0)∪(2;3)∪(3;+∞).
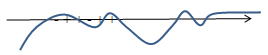
Сурет 22
2. Интервалдар әдісімен параметрі бар бөлшек-рационалды теңсіздіктер
Анықтама.
I. Параметр дегеніміз не?
Анықтама 1. Параметр (грек тілінен. parametron-өлшеу) - мәндері белгілі бір жиынтықтың элементтерін бір-бірінен ажыратуға қызмет ететін шама.
Мысалы, декарттық координаттарда теңдеу y=a ,a≠0, координаттардың басында шыңдары бар барлық параболалардың жиынтығын орнатады. Нақты мағынада a∈(-∞;0)∪(0;+∞) біз осы отбасының параболаларының бірін аламыз.
,a≠0, координаттардың басында шыңдары бар барлық параболалардың жиынтығын орнатады. Нақты мағынада a∈(-∞;0)∪(0;+∞) біз осы отбасының параболаларының бірін аламыз.
Параметрдің тағы бір анықтамасын берейік.
Анықтама 2. Параметр тәуелсіз айнымалы деп аталады, оның мәні есепте берілген тұрақты немесе ерікті нақты Сан немесе алдын ала келісілген жиынға жататын сан болып саналады.
Анықтама 3. Мәндерін өзіміз анықтайтын белгісіз шамалар параметрлер деп аталады.
Параметрлер ретінде қандай белгісіздерді таңдау керек, әдетте өрнекті зерттеу тәсілімен анықталады.
Анықтама 4. Айнымалылармен теңдік берілсін x және а:f(x,a)=0. Егер әрбір нақты мән үшін есеп қойылса а бұл теңдеуді х-ке қатысты шешу үшін f(x;a)=0 теңдеуі деп аталады теңдеу айнымалыға қатысты х және параметр а.
Параметр әдетте латын әліпбиінің бірінші әріптерімен белгіленеді:a,b,c,d,…..
Теңдеу шешілетін айнымалы-алфавиттің соңғы әріптері:x,y,z,t,u,…. .
Анықтама 5.А параметрімен f(x;a) = 0 теңдеуін анықтау өрісі бойынша біз f(x;a) мағынасы бар X және A мәндерінің барлық осындай жүйелерін түсінеміз.
Кейде теңдеуді анықтау аймағы өте оңай орнатылатынын, ал кейде оны нақты түрде жасау қиын екенін ескеріңіз. Содан кейін біз тек теңсіздіктер жүйесімен шектелеміз, оның шешімдерінің жиынтығы теңдеуді анықтау саласы болып табылады. Бұл, әдетте, теңдеуді шешу үшін жеткілікті.
II. "Параметрмен мәселені шешу"нені білдіреді?
Әрине, бұл тапсырмадағы сұраққа байланысты. Егер, мысалы, теңдеуді, теңсіздікті, олардың жүйесін немесе жиынтығын шешу қажет болса, онда бұл кез-келген параметр мәні үшін немесе алдын-ала келісілген жиынға жататын параметр мәні үшін негізделген жауап беруді білдіреді.
Егер теңдеудің, теңсіздіктің және т.б. шешімдерінің жиынтығы жарияланған шартты қанағаттандыратын параметр мәндерін табу қажет болса, онда есептің шешімі көрсетілген параметр мәндерін іздеуден тұрады.
 )(X-
)(X- )(X-
)(X- )<0 x интервалдары үшін, (
)<0 x интервалдары үшін, ( ;
; ), (
), ( ;
; ),
),Ескерту 1.
Сандардың өзі (
 ;
; ),(
),( ;
; ) теңсіздіктің шешімі емес.
) теңсіздіктің шешімі емес.(X-
 )(X-
)(X- )(X-
)(X- )(X-
)(X- )>0
)>0Ескерту 2.
Түр теңсіздіктерінің көптеген шешімдері A(x)≥0 және A(x)≤0 және мұнда,
A(x)=(X-
 ) (X-
) (X- )∙…∙(X-
)∙…∙(X- );
);барлық шешімдердің жиынтығы бар n ≥ 1,n∈N теңсіздіктер A(x)>0 және A(x)<0 және теңдеудің барлық шешімдерінің жиынтығы A(x)=0
Ескерту 4. Егер теңсіздік канондық түрге әкелсе, онда оң жақта"+"белгісі болады.
Ескерту 5. Теңсіздік белгісі "қатаң емес": көпмүшенің немесе нумератордың сандық түзу түбірінде - боялған шеңберлер. "Қатаң" және "қатаң емес" теңсіздіктер үшін бөлгіштің тамыры "бос" .
Бөлшек-рационалды теңсіздіктер.
Анықтама. Бөлшек рационалды түрдің теңсіздігі деп аталады
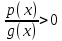 , мұнда p(x) және g(x) - көпмүшелер.
, мұнда p(x) және g(x) - көпмүшелер.Рационалды теңсіздіктерден айырмашылығы, бөлшек рационалдылар айнымалының барлық мәндері үшін анықталмауы мүмкін. Атап айтқанда, мұндай мәндерді қарастырудан алып тастау керек х, онда көпмүше g(x) ол нөлге айналады (өйткені оны нөлге бөлуге болмайды!).
Егер екінші жағынан, барлық рұқсат етілген мәндерде бөлшек рационалды өрнек бар екені анық
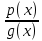
және p(x)*g(x) көбейтіндісінің көпмүшесі бірдей белгіге ие.интервал математический дробный неравенство
2. Шешім алгоритмі
-
Аралық әдіспен бөлшек-рационалды теңсіздікті шешу алгоритмі. Бөлшек рационалды өрнек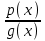 көпмүшеге түрлендіру-
көпмүшеге түрлендіру- 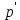 (x)=p(x)∙g(x)
(x)=p(x)∙g(x) -
Көпмүшені төмендетілмейтін факторларға бөлеміз: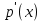 =
=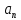 (
( +
+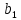 x+
x+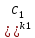 …(
…( +
+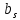 x+
x+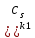 (x-
(x-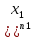 …(x-
…(x-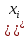
-
Біз екінші ретті төмендетілмейтін факторларды – квадрат триномиалдарды азайтамыз, -
Көпмүшенің тамырларын сандық оське қою, -
Коэффициент белгісіне байланысты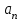 көпмүшенің белгілерін анықтаңыз
көпмүшенің белгілерін анықтаңыз 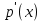 ереже бойынша алынған аралықтарда:
ереже бойынша алынған аралықтарда:
-
оң жақ жартылай интервалда (x>xl) көпмүшенің белгісі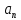 коэффициент белгісімен сәйкес келеді,
коэффициент белгісімен сәйкес келеді, -
сандық ось бойымен солға жылжу. Кезекті XI түбірінен өткенде, көпмүшенің белгісі, егер көбейткіш болса, керісінше өзгереді (x-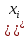 тақ дәрежесі бар
тақ дәрежесі бар 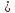 (оның ішінде-бірлік), егер бұл дәреже жұп болса, белгіні сақтаңыз,
(оның ішінде-бірлік), егер бұл дәреже жұп болса, белгіні сақтаңыз, -
c. белгінің қарастырылып отырған теңсіздікте қалай бөлінгеніне байланысты біз жауап ретінде "оң" немесе "теріс" интервалдарды таңдаймыз, -
d. егер теңсіздік қатаң болмаса, жауап ретінде біз көпмүшенің барлық түбірлерін қосамыз p(x), -
e. көпмүшенің барлық түбірлерін жауаптан алып тастауды ұмытпаңыз g(x).
Бөлшек-рационалды теңсіздіктерді шешудің мысалдарын қарастырыңыз.
Мысал 1. Теңсіздікті шешіңіз
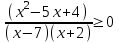 .
.Шешім. 1. Алдымен біз теңсіздіктің рұқсат етілген мәндерінің аймағын табамыз (бұдан әрі қысқартылған түрде жазамыз - рұқсат етілген мәндер аймағы). Әлбетте, бұл
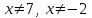 .
.2. Бөлшек-рационалды теңсіздікті рационалдыға айналдырайық:
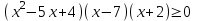 .
.3. Алынған теңсіздіктің сол жағын көбейтейік:
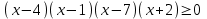 .
.4. Көпмүшенің түбірлері -2, 1, 4 және 7 сандарының "бірлік" еселігі бар екенін ескеріңіз, оларды сандық оське қойып, алынған аралықтарда теңсіздік белгілерін орналастырыңыз:
5. Біз нақты жауапты жазамыз, оның ішінде алымда тұрған көпмүшенің тамыры және бөлгіштің түбірлерін қоспағанда.
Сурет 20
Жауап:
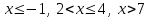 .
.Назар аударыңыз! Жауапты жазу үшін теңсіздіктерді де, бос орындарды да пайдалануға болады. Мысалы, бұл жауапты келесі түрде де жазуға болады:
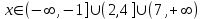 .
.Келесі мысалда біз бірнеше түбірлік теңсіздіктерді қарастырамыз. Мысал 2. Теңсіздікті шешіңіз:
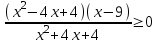 .
.Шешім. Алдымен алымдағы бірінші өрнек пен бөлгіштегі өрнек толық квадраттар екенін ескеріңіз. Келесі: бөлгіш нөлге айналады
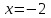 , сондықтан рұқсат етілген мәндер аймағы:
, сондықтан рұқсат етілген мәндер аймағы: 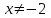 .
.Рационалды теңсіздікке көшейік, аламыз:
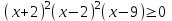 .
.Алынған теңсіздіктің сол жағындағы көпмүшенің тамырларын сандық оське қойып, осы көпмүшенің белгілерін алынған аралықтарда анықтаймыз. -2 және 2 тамырларының еселігін ескере отырып, біз аламыз:
Назар аударыңыз, белгі тек 9-да өзгереді, ал 2 және -2-де ол сақталады, өйткені бұл жұп еселіктің түбірлері.

Сурет 21
Енді жауапты" жинайық": негізгі аралыққа-сәуле
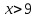 2 және 9 алымдарының түбірлерін қосыңыз, ал бөлгіштің түбірі -2 алынып тасталады. Жауап:
2 және 9 алымдарының түбірлерін қосыңыз, ал бөлгіштің түбірі -2 алынып тасталады. Жауап:
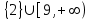 .
.Тағы бір маңызды мысалды қарастырайық, өйткені дәл осындай тапсырмаларда талапкерлер көптеген қателіктер жібереді.
Мысал 3. Теңсіздікті шешіңіз
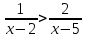 .
.Шешім. Бұл теңсіздік канондық бөлшек рационалға ұқсамайды, бірақ ол төмендейді. Ең бастысы-оны дұрыс жасау. Мұны істеу үшін біз бөлшекті теңсіздіктің оң жағынан солға ауыстырамыз және алынған екі бөлшек айырмашылығын ортақ бөлгішке келтіреміз:
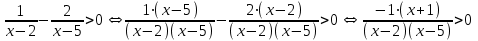 .
.Алымды -1-ге қысқартайық, ал теңсіздік белгісі керісінше өзгереді:
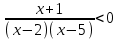 . Енді біздің алдымызда түпнұсқаға тең канондық бөлшек-рационалды теңсіздік тұр. Біз оны интервал әдісімен шешеміз. Жауап:
. Енді біздің алдымызда түпнұсқаға тең канондық бөлшек-рационалды теңсіздік тұр. Біз оны интервал әдісімен шешеміз. Жауап: 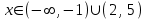 .
.Ескерту. Көбінесе мұндай есептер дұрыс шешілмейді, атап айтқанда: сол жақ бөліктің нумераторын оң жақ бөлгішке көбейту және керісінше. Нәтижесінде мүлдем басқа теңсіздік пайда болады:
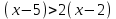 , бұл сызықтық теңсіздікке дейін азаяды
, бұл сызықтық теңсіздікке дейін азаяды 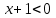 ол үшін жауап:
ол үшін жауап: 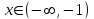 тек ішінара дұрыс сәйкес келеді.
тек ішінара дұрыс сәйкес келеді.Мысал 4.
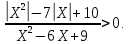
Шешім.Біз теңсіздікті интервал әдісімен шешеміз.Функциялардың нөлдерін табыңыз f(x)=x, модуль белгісімен тұрған: x=0.
1.Егер x≤0, онда теңсіздік форманы алады
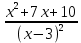 >0,
>0,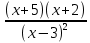 >0.
>0.x∈(-∞;-5)∪(-2;0].
-
Егер x>0, онда теңсіздік келесі формаға ие болады
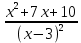 >0,
>0,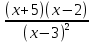 >0
>0x∈(0;2)∪(5;+∞).
Бастапқы теңсіздіктің шешімі бірінші және екінші жағдайларда алынған шешімдердің жиынтығы болып табылады:
x∈(-∞;-5)∪(-2;2)∪(5;+∞).
Жауап: х∈(-∞;-5)∪(-2;2)∪(5;+∞).
Мысал5: Бөлшек рационалды теңсіздікті шешіңіз
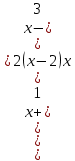 >0
>0Шешім.х=5,x=-1,x=0,x=2,x=3 сандық түзу нүктесінде белгілеп, теңсіздіктің сол жағындағы белгілердің өзгеруін зерттейміз.Теңсіздікті шешу интервалдарды біріктіру болып табылады: (-5;-1)∪(-1;0)∪(2;3)∪(3;+∞).

Сурет 22
2. Интервалдар әдісімен параметрі бар бөлшек-рационалды теңсіздіктер
Анықтама.
I. Параметр дегеніміз не?
Анықтама 1. Параметр (грек тілінен. parametron-өлшеу) - мәндері белгілі бір жиынтықтың элементтерін бір-бірінен ажыратуға қызмет ететін шама.
Мысалы, декарттық координаттарда теңдеу y=a
 ,a≠0, координаттардың басында шыңдары бар барлық параболалардың жиынтығын орнатады. Нақты мағынада a∈(-∞;0)∪(0;+∞) біз осы отбасының параболаларының бірін аламыз.
,a≠0, координаттардың басында шыңдары бар барлық параболалардың жиынтығын орнатады. Нақты мағынада a∈(-∞;0)∪(0;+∞) біз осы отбасының параболаларының бірін аламыз.Параметрдің тағы бір анықтамасын берейік.
Анықтама 2. Параметр тәуелсіз айнымалы деп аталады, оның мәні есепте берілген тұрақты немесе ерікті нақты Сан немесе алдын ала келісілген жиынға жататын сан болып саналады.
Анықтама 3. Мәндерін өзіміз анықтайтын белгісіз шамалар параметрлер деп аталады.
Параметрлер ретінде қандай белгісіздерді таңдау керек, әдетте өрнекті зерттеу тәсілімен анықталады.
Анықтама 4. Айнымалылармен теңдік берілсін x және а:f(x,a)=0. Егер әрбір нақты мән үшін есеп қойылса а бұл теңдеуді х-ке қатысты шешу үшін f(x;a)=0 теңдеуі деп аталады теңдеу айнымалыға қатысты х және параметр а.
Параметр әдетте латын әліпбиінің бірінші әріптерімен белгіленеді:a,b,c,d,…..
Теңдеу шешілетін айнымалы-алфавиттің соңғы әріптері:x,y,z,t,u,…. .
Анықтама 5.А параметрімен f(x;a) = 0 теңдеуін анықтау өрісі бойынша біз f(x;a) мағынасы бар X және A мәндерінің барлық осындай жүйелерін түсінеміз.
Кейде теңдеуді анықтау аймағы өте оңай орнатылатынын, ал кейде оны нақты түрде жасау қиын екенін ескеріңіз. Содан кейін біз тек теңсіздіктер жүйесімен шектелеміз, оның шешімдерінің жиынтығы теңдеуді анықтау саласы болып табылады. Бұл, әдетте, теңдеуді шешу үшін жеткілікті.
II. "Параметрмен мәселені шешу"нені білдіреді?
Әрине, бұл тапсырмадағы сұраққа байланысты. Егер, мысалы, теңдеуді, теңсіздікті, олардың жүйесін немесе жиынтығын шешу қажет болса, онда бұл кез-келген параметр мәні үшін немесе алдын-ала келісілген жиынға жататын параметр мәні үшін негізделген жауап беруді білдіреді.
Егер теңдеудің, теңсіздіктің және т.б. шешімдерінің жиынтығы жарияланған шартты қанағаттандыратын параметр мәндерін табу қажет болса, онда есептің шешімі көрсетілген параметр мәндерін іздеуден тұрады.