Файл: Параметрлі есептерді шешуді дістсілдері.docx

, онда шешім жоқ.

II. 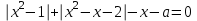теңдеудің 3 түрлі түбірі болатын а параметрінің барлық мәндерін табыңыз.

Шешімі.

Теңдеуді 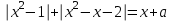қайта жазу арқылы және 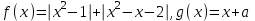функцияларды қарастырғаннан кейін, а параметрінің қажетті мәндері және олар тек 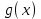функция графигінің ережелеріне сәйкес келетінін байқауға болады, онда 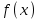функция графигімен дәл үш қиылысу нүктесі болады.

ХОУ координаттар жүйесінде біз 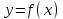функцияның графигін саламыз. Ол үшін оны келесі түрде ұсынуға болады 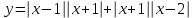және пайда болған төрт жағдайды қарастырғаннан кейін біз бұл функцияны келесідей жазамыз: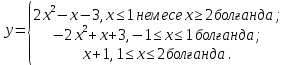



Функция графигі ретінде 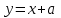- бұл Ох осіне көлбеу бұрышы бар түзу, 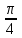-ке тең , және (0;а) координаттары бар нүктеде Оу қиылысатын ось, біз көрсетілген үш қиылысу нүктесін тек осы түзу 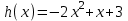функция графигіне тиген жағдайда ғана алуға болады деген қорытындыға келеміз. Сондықтан біз туынды табамыз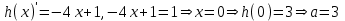

Жауап: .
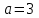III. а параметрінің барлық мәндерін табыңыз, олардың әрқайсысында теңдеулер жүйесі бар

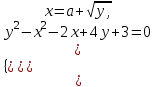
шешімі бар.

Шешімі.

Жүйенің бірінші теңдеуінен 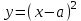аламыз, мұндағы 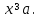Демек, бұл теңдеу "жартылай парабола" отбасын анықтайды- 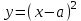параболаның оң жақ тармақтары абсцисса осі бойымен шыңдарды "сырғытады"

---

Екінші теңдеудің сол жағында толық квадраттарды таңдап, оны көбейткіштерге бөлейік

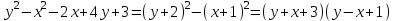
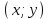жазықтықтың көптеген нүктелерімен, екінші теңдеуді қанағаттандыратын екі түзу 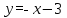және _.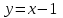

А параметрінің қандай мәндерінде "жартылай парабола" отбасының қисығы алынған түзулердің бірімен кем дегенде бір ортақ нүктеге ие екенін анықтайық.

Егер шыңдары болса жартылай парабола А нүктесінің оң жағында, бірақ В нүктесінің сол жағында (В нүктесі тиетін "жартылай параболаның" жоғарғы жағына тікелей сәйкес келеді 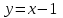), қарастырылып отырған графиктердің ортақ нүктелері жоқ. Егер "жартылай параболаның" шыңы А нүктесіне сәйкес келсе, онда .

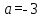"Жартылай Параболаны" түзу сызықпен жанасу жағдайы 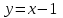біз жүйенің жалғыз шешімінің болу жағдайынан анықтаймыз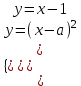

Бұл жағдайда 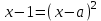теңдеуі біз есептеп шығаратын бір түбірі бар :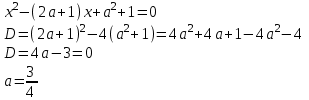



Демек, бастапқы жүйенің а-ның мәнінде 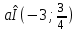шешімдері жоқ, ал 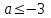_{болғанда, немесе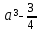} тең болғанда жалғыз шешімі болады.

Жауап: а  (-;-3] ( ;+).
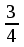IV. Теңдеуді шеш:



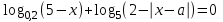
Шешімі.

Келесі теңдеуді қолдана отырып 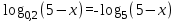, берілген теңдеуді келесі түрде жазамыз: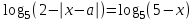

---

Бұл теңдеу жүйеге тең

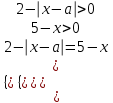
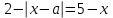теңдеуді келесі түрде жазамыз

. (*)

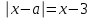Соңғы теңдеуді геометриялық ойларды қолдану арқылы шешу оңай. Функциялардың графиктерін құрайық 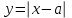и 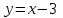. Гррафиктен мынаны аңғаруға болады, 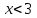болғанда графиктер қиылыспайды. Демек шешім жоқ.

Егер , онда 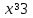болғанда функция графиктері сәйкес келеді және, демек, барлық мәндер 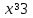тең болғанда теңдеудің шешімдері болып табылады (*).

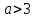тең болғанда графиктер абсцисса болатын 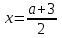бір нүктеде қиылысады. Олай болса, 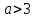болғанда (*) теңдеуі жалғыз шешімге ие болады - .

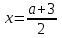Енді біз ( * ) теңдеуінің табылған шешімдері шарттарды қанағаттандыратын а мәндерді зерттейміз

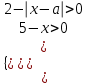
_{болғанда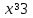}, . Жүйені келесі түрде жазамыз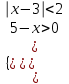



Оның шешімі х (1;5) аралық болады. 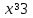_{екенін ескеретін болсақ}, бастапқы теңдеу кезінде барлық мәндер қанағаттандырылады деп қорытынды жасауға болады х аралықтан [3; 5). Келесі жағдайды қарастырайық 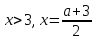. Теңсіздіктер жүйесі келесідей болады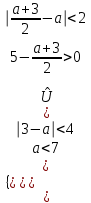

---

Бұл жүйені шеше отырып, а (-1;7) тең екенін анықтаймыз. Бірақ , сондықтан а (3;7) болғанада бастапқы теңдеудің жалғыз шешімі бар .

Жауап:

Егер а (-;3), онда шешім жоқ;

Егере а=3, онда х [3;5);

Егер a (3;7), онда ;

Егер a [7;), онда шешім жоқ.
V. Теңдеуді шешіңіз

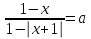, мұнда а - параметр. (5)
Шешімі.

1. 
   а-ның кез-келген мәнінде :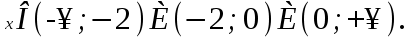
   
2. 
   Егер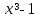 , онда ;
   

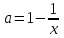егер 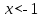, онда .

3. 
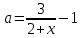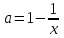   функцияның графигін құрамыз, біз оның бір бөлігін ерекшелейміз, 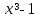_{сәйкес келеді}. Содан кейін функция графигінің сол бөлігін белгілеңіз 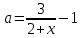, 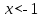_{-ге сәйкес келеді}.
   

4. График бойынша біз (5) теңдеудің қандай мәндерде шешімі бар екенін және қайсысында шешімі жоқ екенін анықтаймыз.

Жауап:

егер 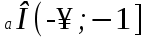, онда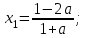

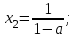
егер 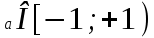, онда ;

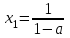егер ,

---

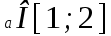онда шешім жоқ;

егер 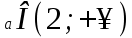, онда , .

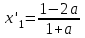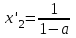VI. Бұл параметр мәндері қандай шарттарды қанағаттандыруы керек 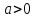және 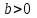, жүйелер болған кезде

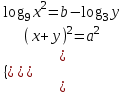(1)

және

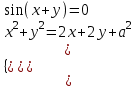(2)

шешімдердің саны бірдей?
Шешімі.

Осыны ескере отырып 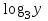тек мағынасы бар 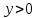, трансформациядан кейін жүйені аламыз

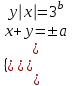(3)

эквивалентті жүйе (1).

Жүйе (2) жүйеге тең

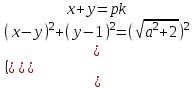(4)

Жүйенің бірінші теңдеуі (4) хОу жазықтығында түзулер тобын, екінші теңдеу А(1;1) нүктесінде центрі және 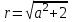радиусы бар концентрлік шеңберлер тобын анықтайды.

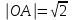болғандықтан, ал 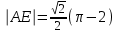, онда 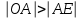, және, демек, жүйеде (4) кем дегенде төрт шешім бар. 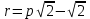болғанда, шеңбер түзу сызыққа тиеді 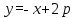ал (4) жүйеде бес шешім бар.

Олай болса, егер 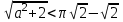, онда (4) жүйе төрт шешімге ие, егер 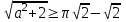, мұндай шешімдер төртеуінен көп болады.

Егер шеңберлердің радиустарын емес, а параметрінің өзін ескеретін болсақ, онда жүйе (4) жағдайда төрт шешімге ие, 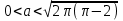болғанда, және төрт шешімнен артық, егер .

---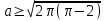