ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 180
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рациональные алгебраические уравнения с параметрами.
1. P(x, a) = x - |a| = 0. а параметрінің әрбір мәні үшін теңдеуді шешіңіз.
Сурет -1
Шешім: бастау үшін модульді оң жаққа жылжытыңыз:
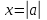 . Енді біз модульдің анықтамасын қолданамыз және жүйені жазамыз:
. Енді біз модульдің анықтамасын қолданамыз және жүйені жазамыз: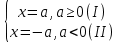
Екі жағдайды талдайық:
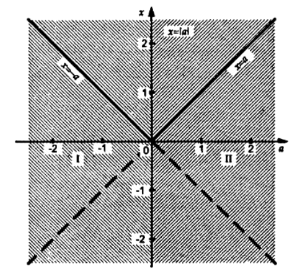
1. x = |a| функция графигі, мұнда a параметрі – аргумент, 1-суретте көрсетілген. График-көлденең параметрлік осі Oa бар xoy координаталық-параметрлік жазықтығындағы барлық нүктелердің жиынтығы (Х, a), олардың әрқайсысының координаталық мәндері мен параметрлері алынған жүйені қанағаттандырады. XОУ координаталық-параметрлік жазықтығының нүктелері, координаталық мәндер және олардың әрқайсысының параметрлері (I) өрнегін қанағаттандырады, жартылай жазықтықта орналасқан х = a түзу бөлігінде орналасқан a ≥ 0 шекарамен a = 0 (1-сурет).
Сол сияқты біз (II) өрнегінің шешімін табамыз. Нүктелер a < 0 жартылай жазықтығында орналасқан X = -a түзу бөлігінде орналасқан (1 – сурет).
Осылайша, а параметрінің әрбір мәні x координатының жалғыз мәніне сәйкес келеді. Егер a < 0, онда x = -a, егер a = 0, онда x = 0, егер a > 0, онда x = a.

Сурет -2
2. 2-суретте бірдей жиын бейнеленген, бірақ Oa тік параметрлік осі бар aox координаталық-параметрлік жазықтығында. а = const түзулерінің әрқайсысы бастапқы теңдеудің шешімін анықтайтын x координатасы бар нүктеде бейнеленген жиынды қиып өтеді.
Егер a = const < 0, онда x = -a, егер a = const = 0, онда x = 0, егер a = const > 0, онда x = a. Осылайша, біз бірінші жағдайдағыдай жауап аламыз.
Жауап: Егер a < 0,онда x = -a, егер a = 0, онда x = 0, егер a > 0, онда x = a.
2. 3|x+2a| - 3a + x – 15 = 0.
а параметрінің қандай мәндерінде теңдеудің барлық шешімдері 4 ≤ x ≤ 6 теңсіздікті қанағаттандырады?
Шешім: біз модульді ашамыз, екі жүйенің жиынтығын аламыз:
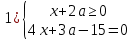
2)
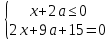
Бұл нөмірде тікелей x + 2a = 0 xoa координаталық-параметрлік жазықтығын екі "жартылай аймаққа" бөледі 1) және 2).
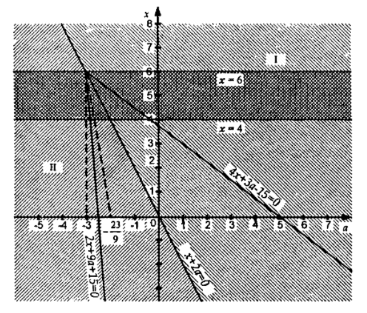
Сурет 3
Шартты қанағаттандыратын 1) жүйенің шешімімен 4 ≤ x ≤ 6, координаталық-параметрлік жазықтықта нүктеде басы бар сәуленің сегменті болады a = -3, x = 6 және соңында a =
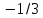 , x = 4 (а табу үшін х мәндері теңдеуге ауыстырылады).
, x = 4 (а табу үшін х мәндері теңдеуге ауыстырылады). Сол сияқты біз жүйенің шешімін табамыз
2). Бұл нүктеде басы бар сәуле сегменті a = -3, x = 6 и a =
 , x = 4 (бұл сегменттер қалың сызықтармен 4 суретте көрсетілген).
, x = 4 (бұл сегменттер қалың сызықтармен 4 суретте көрсетілген).Екі шешім де сегменттегі а параметрінің барлық мәндеріндегі теңсіздікті қанағаттандырады [-3;
 ].
].Жауап: -3 ≤ a ≤
 .
.3. (2–x)(x+a) = 0. Теңдеудің екі түрлі теріс емес түбірі бар а параметрінің барлық мәндерін табыңыз.
Шешім: ХОa координаталық-параметрлік жазықтығында барлық нүктелер жиынтығы (х, a), координаталық мәндер және олардың әрқайсысының параметрлері берілген теңдеуді қанағаттандырады, парабола-функцияның графигі
a = (2-x)(x+1)
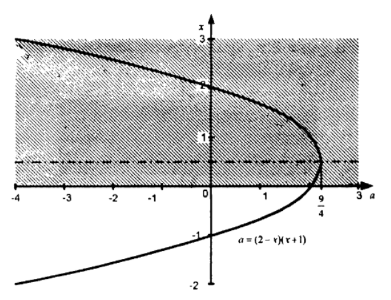
Сурет -4
Парабола нүктелерде Ox осін кесіп өтеді x = -1, a = 0 и x = 2, a = 0. Параболаның төбелері x = 1/2, a = 9/4 екі түбірі де сәйкес келеді. 2 ≤ a ≤ 9/4 болғанада, екі түбір де теріс емес.
Рациональные алгебраические неравенства с параметрами.
4. X - |a| > 0. А параметрінің әрбір мәні үшін теңсіздікті шешіңіз.
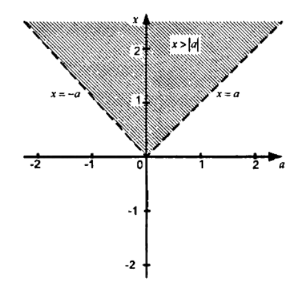
Сурет -5
Шешім: 5-суретте xoy координаталық-параметрлік жазықтығында (x, a) көптеген нүктелер бейнеленген, олардың әрқайсысының координаталық мәндері мен параметрлері берілген теңсіздікті қанағаттандырады. Функция графигінің үстінде орналасқан нүктелер x = |a|, бұл жиынның элементтері.
А параметрінің әрбір мәні қажетті координат мәндерімен бейнеленген жиынның нүктелеріне сәйкес келеді.
Жауап: Егер a < 0, онда x > -a, егер a = 0, онда x > 0, егер a > 0, онда
x > a.
5. Теңсіздік болатын a параметрінің барлық мәндерін табыңыз
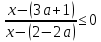 барлық x үшін 2 ≤ x ≤ 3орындалады.
барлық x үшін 2 ≤ x ≤ 3орындалады.Шешімі:Теңсіздікті шешейік F(x, a) =
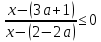
Координаталық-параметрлік жазықтықта түзу x = 3а + 1 нумератор нөлге, ал бөлгіш x = 2–2a-ға айналады. Бұл түзулер координаталық-параметрлік жазықтықты төрт "ішінара аймаққа"бөледі.
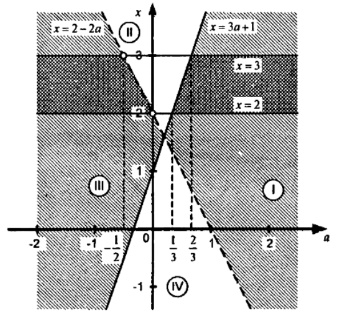
Сурет - 6
Енді біз әр аймақтағы белгілерді анықтауымыз керек, ол үшін зерттелетін аймақтан кез-келген нүктені алу керек. Мысалы, x=2, a=1 F(2, 1) > 0. Демек, барлық жерде І облыста F(x, a) > 0. Қалған аймақтарда біз белгілерді ұқсастық бойынша анықтаймыз. Осылайша, теңсіздік I және III облыстарда орындалады, x=3а+1 шекарасы оның шешімі болып табылады, ал х=2-2a шекарасы қарастырылып отырған теңсіздіктің көптеген шешімдеріне жатпайды.
Берілген жиынның 2 ≤ x ≤ 3 теңсіздігін қанағаттандыратын нүктелер жиынымен қиылысуы берілген теңсіздіктің 2 ≤ x ≤ 3 аралығындағы шешімін береді. Демек, берілген теңсіздік a < -1/2 және a ≥ 2/3 кезінде 2 ≤ x ≤ 3 аралығындағы барлық x үшін бірден орындалады.
Жауап: a < -1/2, a ≥ 2/3.
6. Q параметрінің әрбір бүтін мәні үшін x2-5(x-1)+3|x-q|-q ≤0 теңсіздігінің бүтін шешімдерін табыңыз.
Шешім: екі жүйеден тұратын эквивалентті жиынтық құрайық:
1)
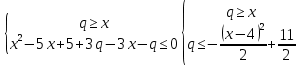
2)
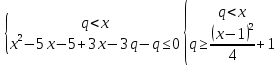
ХОУ координаталық-параметрлік жазықтығында алынған теңсіздік жүйелерінің жиынтығын қанағаттандыратын мәндер жиыны (x, q) екі параболамен шектеледі. Шыңдарда парабола x= 1, q=1 және x = 4, q=11/2. Біз бұл жиынды xm координаталары мен qn параметрінің бүтін мәндері бар тікбұрышты тормен жабамыз: 1 ≤ xm ≤ 5, 1 ≤ qn ≤ 6.
Біз торлы тіктөртбұрыштың түйіндеріндегі барлық нүктелер жиынтығының ішінен көлеңкеленген жиынға жататын нүктелерді табамыз, яғни. координаталық-параметрлік жазықтықта теңсіздіктің бүтін шешімдерін береді (7 – суретте бұл нүктелер қалың, ал шешім бермейтін нүктелер квадраттармен бейнеленген)
.
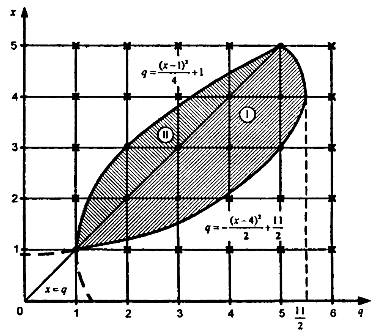
Сурет 7
Жауап: Егер q=1, онда x=1;
егер q=2, онда x=2, x=3;
егер q=3, онда x=2, x=3;
егер q=4, онда x=3, x=4
егер q=5, онда x=3, x=4, x=5.
7. Теңсіздіктер жүйесі болатын барлық а мәндерін табыңыз
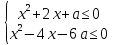 жалғыз шешімі бар.
жалғыз шешімі бар.Шешім: ХОa координаталық-параметрлік жазықтықта берілген теңсіздіктер жүйесінің шешімі I және II жиындардың қиылысы болып табылады. I жиын a = -x2 – 2x (1) (1) параболасында және оның сол жағында орналасқан жазықтықтың барлық нүктелерінен тұрады, ал II жиын a = 1/6 ∙ (x2-4x) (2) параболасында және оның оң жағында орналасқан нүктелерден тұрады.
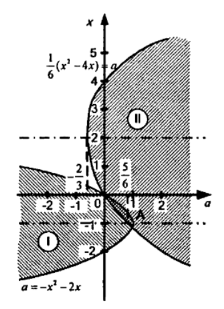
Сурет 8
Параболалар (1) және (2) олар үшін нүктелерде қиылысады x = 0, a = 0 және x = -8/7 < -1 және a = 48/49 < 1.
А парабола төбесінде (1) x = -1, a=1.
O және A нүктелері сәйкесінше теңсіздіктер жүйесінің алынған шешімдер жиынтығының ең сол және оң нүктелері болып табылады.
Демек, a < 0 және a > 1-де берілген теңсіздіктер жүйесінің шешімдері жоқ; a = 0 және a = 1-де-жалғыз шешімі бар; 0 < a < 1 – де-шешімдердің шексіз жиынтығы.
Жауап: a = 0, a = 1.
Иррациональные уравнения и неравенства с параметрами.
8. а параметрінің әрбір мәні үшін теңдеуді шешіңіз
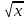 =a.
=a.Шешім: квадрат арифметикалық түбірді анықтау арқылы жүйені құруға болады:
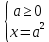
XОа координаталық-параметрлік жазықтығында бастапқы рационалды теңдеудің шешімі-оң жақ жарты жазықтықта орналасқан x = a2 параболасының бөліктерінде орналасқан осы жазықтықтың нүктелерінің жиынтығы a ≥ 0.
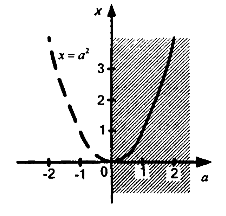
Сурет 9
Жауап: Егер a < 0, онда шешім жоқ, егер a ≥ 0, онда x = a2.
9. а параметрінің қандай мәндерінде теңдеу
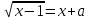 шешімі болады?
шешімі болады?Шешімі:
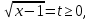 болсын, берілген өрнекті квадраттайық:
болсын, берілген өрнекті квадраттайық: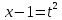 . Алынған өрнектен
. Алынған өрнектен
x: x = t2 + 1 айнымалысын білдіреміз. Енді сіз жүйені жасай аласыз:
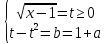
tOb координаталық-параметрлік жазықтығында қалың сызық жүйенің шешімін көрсетеді.
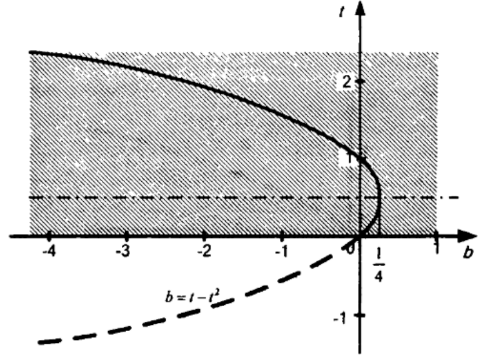
Сурет 10
Бастапқы теңдеудің шешімі бар
b = 1+a ≤ 1/4
a ≤ -3/4
Жауап: a ≤ -3/4.
10. Теңсіздікті шешіңіз
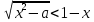 а параметрінің барлық мәндері үшін.
а параметрінің барлық мәндері үшін.Шешімі: Жүйені құрайық:
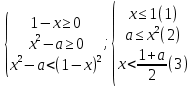
XОa координаталық-параметрлік жазықтығында алынған жүйенің шешімі (x,a) нүктелерінің жиыны болып табылады, бір уақытта түзу сызықтан төмен орналасқан x = 1 және оған, параболада a = x2 және оның сол жағында, түзу сызықтан төмен
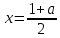 .
.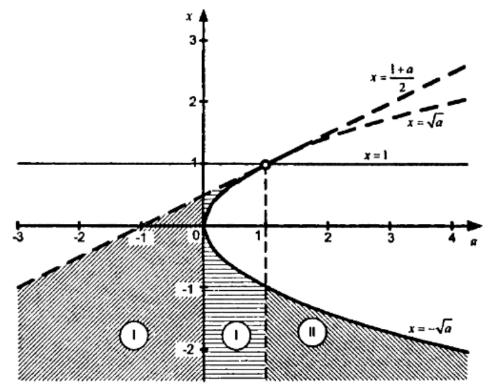
Сурет 11
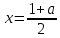 түзуі a = x2 параболаға қатысты Шартта анықталған параметрдің координаты мен мәні бар нүктеде
түзуі a = x2 параболаға қатысты Шартта анықталған параметрдің координаты мен мәні бар нүктеде
Параболаның жоғарғы және төменгі тармақтарының теңдеулері a = x2 түрі бар
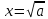 және
және 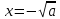 .
.11-суретте көптеген шешімдер штрихталған.
Жауап: Егер a ≤ 0, онда
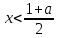 ; егер 0 < a < 1, онда
; егер 0 < a < 1, онда 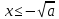 ,
, 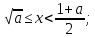 егер a ≥ 1, онда
егер a ≥ 1, онда 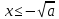 .
.11. Теңсіздікті шешіңіз
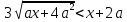 а параметрінің барлық мәндері үшін.
а параметрінің барлық мәндері үшін. 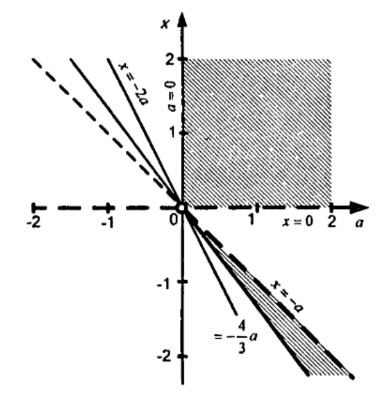
Сурет 12
Шешім: жүйені құрайық: