Файл: На какие группы делятся средние величины.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 06.12.2023

Просмотров: 338

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Блок 1

  1. На какие группы делятся средние величины?



Средняя величина — это обобщающий показатель, характеризующий типический уровень явления в конкретных условиях места и времени. Средняя величина всегда обобщает количественную вариацию признака. Средняя в отличие от простой абсолютной величины позволяет сравнивать общий уровень признака у единиц, относящихся к разным совокупностям.

Все средние величины разделяются на два больших класса:

  • 1) степенные средние, к которым относятся прежде всего наиболее известные и часто применяемые виды средних. Это средняя арифметическая, средняя квадратическая и средняя геометрическая величины;

  • 2) структурные средние величины, в качестве которых рассматриваются мода и медиана.

Степенные средние величины исчисляются в двух формах — простой и взвешенной. Простая средняя величина имеет следующий общий вид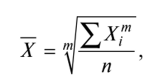



где X• — варианта (значение) осредняемого признака; т — показатель степени средней; п — число вариант (наблюдений).

Взвешенная средняя величина считается по сгруппированным данным, представленным в виде дискретных или интервальных рядов распределения: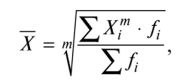



где Xj — варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта; т — показатель степени средней; ft — частота, показывающая, сколько раз встречается /-е значение осредняемого дискретного признака или количество попаданий признака в /-й интервал.
Формулы расчета степенных средних включают показатель степени (т). В зависимости от его значения различается:

  • • средняя гармоническая, если т = -1;

  • • средняя геометрическая, если т = 0;

  • • средняя арифметическая, если т= 1;

  • • средняя квадратическая, если т = 2;

  • • средняя кубическая, если т = 3 и т.д.
Если рассчитать все виды средних для одних и тех же исходных данных, то их значения окажутся неодинаковыми. Здесь действует правило мажорантности: с возрастанием показателя степени т увеличивается и соответствующая средняя величина:

  1. При каких условиях используются средние степенные простые величины?
Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных. Потребность определения средних величин связана с тем, что у различных единиц исследуемых совокупностей индивидуальные значения одного и того же признака, как правило, неодинаковы.

  1. При каких условиях требуется использование средних степенных взвешенных величин?
Ответ: Если данные представлены первичным признаком (потому что показатели, выраженные превичным признаком, могут быть непосредственно измерены сосчитаны), если данные с группированы в вариационных рядах распределения.

  1. В чем отличие и сходство средней арифметической взвешенной и средней гармонической взвешенной?

    Средняя арифметическая взвешенная, используется, когда в задаче есть знаменатель(fi), а средняя гармоническая взвешенная используется, когда есть числитель. Обе формулы используются при наличие у показателя вторичного признака

  1. Что такое дисперсия? В чем измеряется?
Дисперсия- средняя величина из квадратов отклонений значений признака от средней величины. Дисперсия считается безмерной величиной.Из за трудности интерпретации дисперсии переходят от дисперсии к среднему квадратическому отклонению:Среднее квадратическое отклонениеизмеряется в единицах исходной информации

  1. В чем различие в использовании простой и взвешенной формулы для расчета дисперсии?
Степенные средние могут быть простыми и взвешенными.Простая средняя величина рассчитывается при наличии двух и более несгруппированных
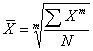
 статистических величин, расположенных в произвольном порядке по следующей общей формуле:Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:

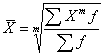
  1. Что такое среднее квадратическое отклонение? В чем его преимущество перед дисперсией?
Среднеквадратическим отклонением называют значение квадратного корня из дисперсии случайной величины D. Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные значения признака от среднего их значения.Преимущество среднего квадратического отклонения перед дисперсией состоит в том, что оно является именованной величиной, т.е. имеет ту же единицу измерения, что и значения признака.

  1. Что такое коэффициент вариации? В чем измеряется? Для чего используется?
В теории вероятности и статистике, коэффициент вариации, также известный как относительное стандартное отклонение, это стандартная мера дисперсии распределения вероятностей или частотного распределения. Она часто выражается в процентах и определяется как отношение стандартного отклонения σ к среднему μ. КВ или СОО широко используются в аналитической химии для выражения точности и повторяемости анализа. Они также часто применяются в инженерии и физике, при проведении исследований по обеспечению качества. Кроме того, КВ используется экономистами и инвесторами в экономических моделях.

  1. Что такое ряд динамики? Из каких элементов состоит?
Ряд динамики (хронологический, динамический, временной) – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Ряд динамики состоит из двух элементов: 1) периодов или моментов времени (t); 2) уровней изучаемого показателя (у).

  1. Какие типы рядов динамики бывают?

  • По времени — ряды моментные и интервальные (периодные), которые показывают уровень явления на конкретный момент времени или на определенный его период. Сумма уровней интервального ряда дает вполне реальную статистическую величину за несколько периодов времени, например, общий выпуск продукции, общее количество проданных акций и т.п. Уровни моментного ряда, хотя и можно суммировать, но эта сумма реального содержания, как правило, не имеет. Так, если сложить величины запасов на начало каждого месяца квартала, то полученная сумма не означает квартальную величину запасов.

  • По форме представления — ряды абсолютных, относительных и средних величин.

  • По интервалам времени — ряды равномерные и неравномерные (полные и неполные), первые из которых имеют равные интервалы, а у вторых равенство интервалов не соблюдается.

  • По числу смысловых статистических величин — ряды изолированные и комплексные (одномерные и многомерные). Первые представляют собой ряд динамики одной статистической величины (например, индекс инфляции), а вторые — нескольких (например, потребление основных продуктов питания).

  1. Что такой абсолютный прирост? Чем отличаются цепные и базисные абсолютные приросты?
Абсолютный прирост – характеризует изменение показателя за один или несколько последовательных периодов времени в абсолютном выражении;Измеряется в тех же единицах, что и исходная информация Может быть как положительная, так и отрицательнаяАбсолютный прирост называется цепным если за базу сравнения принят уровень предыдущего периодаБазисный прирост называется базисным если за базу сравнения принят какой либо определенный уровень, (чаще начальный)

  1. Что такое темп роста? Чем отличается от коэффициента роста?
Темп роста (Тр) — это показатель интенсивности изменения уровня ряда, который выражается в процентах, определяет общую динамику показателя за один или несколько последовательных периодов времени, а в долях выражается коэффициент роста (Кр). Коэффициент роста определяется как отношение последующего уровня к предыдущему или к показателю принятому за базу сравнения. Он определяет, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения- какую часть базисного уровня составляет сравниваемый.Темп роста всегда положительный. Расчеты темпа роста: цепной, базисный

  1. Как проявляется взаимосвязь между цепными и базисными темпами роста?


Между базисными и цепными темпами роста, выраженными в форме коэффициентов, имеется определенная взаимосвязь, которая заключается в следующем:• во-первых, произведение последовательных цепных темпов роста равно базисному темпу роста за соответствующий период;• во-вторых, частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.Указанные зависимости между темпами роста можно использовать для преобразования базисных темпов в цепные и наоборот, особенно в тех случаях, когда неизвестны абсолютные уровни динамики.

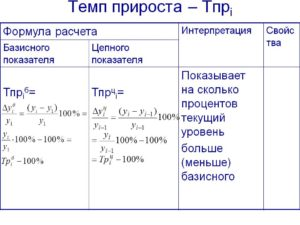
  1. Что такое темп прироста? Как рассчитывается?
Темп прироста – относительная величина прироста, то есть отношение абсолютного прироста к предыдущему или базисному уровню. Характеризует, на сколько процентов уровень данного периода больше (или меньше) базисного уровня.

  1. В чем отличие в интерпретации темпов роста и темпов прироста?
Темп роста – относительный экономический показатель, показывающий процентный рост одного показателя над аналогичным показателем прошлого периода. Темп прироста – самый универсальный сравнительный показатель эффективности, он показывает, НА СКОЛЬКО процентов вырос или снизился один показатель по сравнению с аналогичным показателем более раннего периода.

  1. Почему для первого уровня ряда во временном ряду цепные показатели (абсолютный прирост, темп роста, темп прироста) невозможно рассчитать?
Потому что цепной показатель рассчитывается в пределах исследуемого промежутка, т.к. это первый уровень, то это начало промежутка, цепной показатель не рассчитать из-за отсутствия уровня перед ним.

  1. Чему равен базисный абсолютный прирост для первого года (даты) во временном ряду?
Базисный абсолютный прирост – разность между сравниваемым уровнем ряда   и уровнем, принятым за постоянную базу сравнения  :  Равен 0,0

  1. Чему равен базисный темп роста для первого года (даты) во временном ряду?
Темп роста базисный – отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения. В данном случае равен 100%.

  1. От чего зависит расчет среднего уровня ряда?


Каждый ряд динамики можно рассматривать как некую совокупность n меняющихся во времени показателей, которые можно обобщать в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении изменений того или иного показателя в разные периоды, в разных странах и т.д.Обобщенной характеристикой ряда динамики может служить прежде всего средний уровень ряда. Способ расчета среднего уровня зависит от того, моментный ряд или интервальный (периодный).В случае интервального ряда его средний уровень определяется по формуле простой средней арифметической величины из уровней ряда.

Смотрите также файлы