ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 80
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ответ: выберем формулу средней арифметической взвешенной, так как известен знаменатель логической формулы.
-
Известны доли численности детей в общей численности населения (в %) по городам и общая численность населения по городам, по какой формуле будет рассчитана средняя доля численности детей?
Ответ: средняя доля численности детей будет рассчитана по формуле средней арифметической взвешенной, так как известен знаменатель логической формулы.
-
Имеются данные о налогах на продукты в млрд. руб. по регионам, в чем будет измеряться среднее значение налогов на продукты и дисперсия?
Ответ: среднее значение налогов на продукты будет измеряться в млрд. руб., дисперсия единицы измерения не имеет.
-
Имеются данные о численности рабочей силы в тыс. чел. по регионам, в чем будет измеряться среднее значение численности рабочей силы и среднее квадратическое отклонение?
Ответ: среднее значение численности рабочей силы и среднее квадратическое отклонение будут измеряться в тыс. чел.
-
Если коэффициент вариации равен 15%, что можно сказать о средней величине?
Ответ: средняя величина является типичной и достоверной характеристикой для исследуемой совокупности.
-
Если коэффициент вариации равен 56%, что можно сказать о средней величине?
Ответ: средняя величина является нетипичной и недостоверной характеристикой для исследуемой совокупности
-
Если средняя величина равна 10 рублям, а среднее квадратическое отклонение – 3 рублям, какой будет формулировка вывода по этим показателям?
Ответ: в среднем конкретные значения признака отклоняются от их среднего значения (10 рублей) на 3 рубля в ту или иную сторону, наиболее характерные значения признака находятся в пределах от 7 до 13 руб. (диапазон
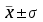 ).
).-
Представлен временной ряд, составленный по показателю «наличие основных фондов на конец года, млрд. руб.», с 2015 по 2019 гг. Что будет написано в итоговой строке по этому показателю?
Ответ: будет написан «–» (прочерк) или знак Х, так как показатели моментных рядов не обладают свойством суммирования.
-
Представлен временной ряд, составленный по показателю «объем прямых иностранных инвестиций, млн. руб.», с 2015 по 2019 гг. Что будет написано в итоговой строке по этому показателю?
Ответ: сумма показателей ряда динамики (так как ряд интервальный).
-
Чем по временным характеристикам отличаются показатели «численность населения на 1 января» и «валовая добавленная стоимость»?
Ответ: «численность населения на 1 января» – развитие явления на определенную дату (моментный ряд динамики); валовая добавленная стоимость» – развитие явления за определенный интервал времени – месяц, квартал, год (интервальный ряд динамики).
-
Сумма приростов численности населения в тыс. чел. к предыдущему году (за 2014, 2015, 2016, 2017 годы) равна 30,5 тыс. чел. Чему равен прирост численности населения в тыс. чел. к 2013 году?
Ответ: 30,5 тыс. чел.
Сумма цепных абсолютных приростов за период равна базисному приросту последнего периода ряда динамики за этот же период.
-
Временной ряд включает в себя 7 уровней, сколько цепных абсолютных приростов можно посчитать?
Ответ: 6.
-
Временной ряд включает в себя 8 уровней, сколько базисных абсолютных приростов можно посчитать?
Ответ: 8, если считать абсолютный прирост базисного года, равный нулю.
-
Временной ряд включает в себя 5 уровней, сколько темпов роста, % к предыдущему году можно рассчитать для данного временного ряда?
Ответ: 4.
-
Временной ряд включает в себя 10 уровней (с 2010 г. по 2019 г.), сколько темпов роста, % к 2010 г. можно рассчитать?
Ответ: 10, если считать базисный темп роста 2010 года, равный 100%.
-
Временной ряд включает в себя 7 уровней, сколько темпов прироста, % к предыдущему году можно рассчитать для данного временного ряда?
Ответ: 6.
-
Имеется показатель «численность населения на 1 января, тыс. чел», в чем будет измеряться абсолютное значение 1% прироста?
Ответ: в тыс. чел.
-
Темп роста численности населения в 2018 г. составил 102,3%, какой можно сделать вывод?
Ответ: численность населения в 2018 г. увеличилась на 2,3%.
-
Число больничных коек в 2019 г. выросло на 5,4%, чему равен темп роста числа больничных коек в 2019 г.?
Ответ: 105,4%.
-
Темп роста численности рабочей силы составил 98,8%, какой вывод можно сделать?
Ответ: численность рабочей силы снизилась на 1,2%.
-
Численность занятых уменьшилась на 5,4%, чем равен темп роста численности занятых?
Ответ: 94,6%.
-
Имеются данные о ценах на 5 товаров, сколько индивидуальных индексов цен и физического объема можно рассчитать?
Ответ: 10 индексов всего: 5 индивидуальных индексов цен и 5 индивидуальных индексов физического объема.
-
Имеются данные о ценах на 5 товаров, сколько общих индексов цен и физического объема можно рассчитать?
Ответ: 2 общий индекса: 1 общий индекс цен и 1 общий индекс физического объема.
-
Если в сентябре общий индекс цен в регионе составил 103,4%, какой вывод можно сделать об изменении цен?
Ответ: в сентябре цены в среднем в регионе выросли на 3,4%.
-
Если средний уровень цен на товары и услуги в июне по сравнению с маем снизился на 3,7%, то чему равен общий индекс цен?
Ответ: 0,963 (96,3%)
-
Если дисперсия равна 1000, что можно сказать о изучаемой совокупности?
Ответ: дисперсия – это средний квадрат отклонений значений признака от их средней величины. Дисперсия еще не дает представления об однородности совокупности, этому показателю трудно дать экономическую интерпретацию, так как он рассчитан в квадратных единицах. Для того, чтобы судить об изучаемой совокупности, нужно рассчитать среднее квадратическое отклонение:
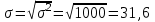
В изучаемой совокупности в среднем конкретные значения признака отклоняются от их среднего значения на 31,6 в ту или иную сторону.
-
Рассчитана средняя цена на яблоки, и она измеряется в рублях, в чем будет измеряться коэффициент вариации?
Ответ: в процентах.
-
Если общий индекс физического объема равен 98,7%, что можно сказать о динамике количества производимых товаров?
Ответ: количество производимых товаров в среднем снизилось на 1,3%.
-
Если общий индекс цен составил 102,5%, а индивидуальный 99,8%, если ли в этом противоречие? Какой вывод можно сделать?
Ответ: нет противоречия. Индивидуальные индексы характеризуют изменение отдельных единиц статистической совокупности, а общий индекс характеризует изменение по всей совокупности элементов сложного явления.
Цена отдельного товара могла снизиться на 0,2% (индивидуальный индекс 99,8%), а другого – увеличиться. Общий индекс цен, равный 102,5% показывает, что в среднем цены на несколько товаров выросли на 2,5%, несмотря на то, что цена одного товара снизилась на 0,2%.
БЛОК 3
-
На предприятии работают 15 работников с заработной платой 25700 руб., 5 работников с заработной платой 23400 руб., 2 работника с заработной платой 23950 руб. и 2 работника с заработной платой 24 тыс. руб. Чему равна средняя заработная плата на данном предприятии?
Решение:
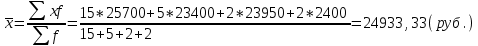
-
Известно, что общий выпуск продукции на 1 предприятии составил 100 тыс. руб., на втором – 150 тыс. руб., цена продукции 1 предприятия равна 100 рублей, 2 предприятия – 105 рублей. Чему равна средняя цена по двум предприятиям?
Решение:
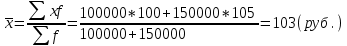
-
В интервале от 10 до 20 тыс. руб. находилась заработная плата 15 работников, в интервале от 20 до 40 тыс. руб. – 20 работников, в интервале от 40 до 60 тыс. руб. – 5 работников. Чему равна средняя заработная плата всех работников?
Решение:
Найдем средину интервалов
1)(10+20)/2=15тыс.руб.
2)(20+40)/2=30тыс.руб.
3) (40+60)/2=50тыс.руб.
Средняя заработная плата всех работников составит
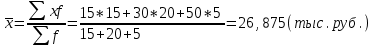
-
Если темп роста равен 110% за 4 года, чему равен средний темп роста в этот период?
Решение:
Средний темп роста равен
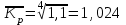
-
Временной ряд состоит из 5 уровней, уровень первого периода = 100 млн. руб., уровень последнего периода = 120 млн. руб., чему равен средний темп роста?
Решение:
Средний темп роста равен
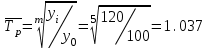
-
Временной ряд состоит из 5 уровней, уровень первого периода = 100 млн. руб., уровень последнего периода = 120 млн. руб., чему равен базисный абсолютный прирост последнего периода и среднегодовой абсолютный прирост?
Решение:
Базисный абсолютный прирост равен:
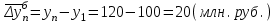
Среднегодовой абсолютный прирост равен
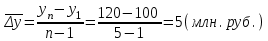
-
На 1 января товарные запасы оценивались в 300 тыс. руб., на 1 февраля – 320 тыс. руб., на 1 марта – 325 тыс. руб., на 1 апреля – 280 тыс. руб. Чему равен средний уровень товарных запасов в 1 квартале года?
Решение:
Средний уровень товарных запасов в 1 квартале будет определятся по формуле средней арифметической взвешенной, так как промежутки между датами не равные:
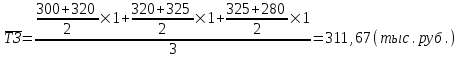
-
На 1 января численность населения города была 105,9 тыс. чел., на 1 марта – 105,7 тыс. чел., на 1 августа – 106,1 тыс. чел., на 1 января следующего года – 106,4 тыс. чел. Чему равна среднегодовая численность населения города?
Решение:
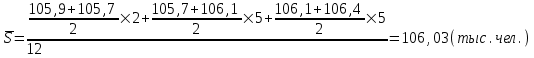
-
Коэффициенты роста к предыдущему году составили: в 2014 г. – 1,004 в 2015 г. -1,021, в 2016 г. – 1,033, в 2017 г. – 1,089. Чему равен базисный темп роста в 2017 г. (к 2013 г.)?
Решение:
Коэффициент роста рассчитывается
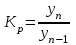
Темп роста рассчитывается:
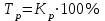
Следовательно:
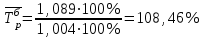
-
Коэффициенты роста к предыдущему году составили: в 2014 г. – 1,004 в 2015 г. -1,021, в 2016 г. – 1,033, в 2017 г. – 1,089. Чему равен средний темп роста в 2014-2017 гг.?
Решение:
Средний темп роста равен
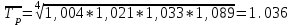
-
Оборот розничной торговли в мае составил 150 тыс. руб., в июне – 200 тыс. руб. Чему равен сводный индекс оборота товаров?
Решение:
Сводный индекс оборота товаров:
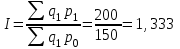
-
Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Чему равен общий индекс цен?
Решение:
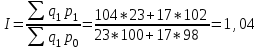
В среднем цены увеличились на 4%
-
Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Чему равен общий индекс физического объема?
Решение:
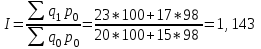
В среднем физический объем увеличились на 14,3%
-
Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Чему равен общий индекс оборота товаров?
Решение:
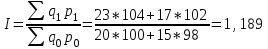
В среднем товарооборот увеличились на 18,9%
-
Цена товара А в январе составила 100 рублей, в феврале – 104 рубля. Цена товара Б в январе – 98 руб., в феврале – 102 руб. В январе было продано товара А – 20 шт., товара Б – 15 шт., в феврале – 23 и 17 шт. соответственно. Рассчитайте индивидуальные индексы цен?