ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 97
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
; 

 ;
; 
 , отсюда
, отсюда
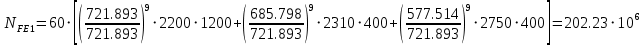
для колеса :
:
 ;
;  ;
; 

 ;
; 

 ;
; 
 , отсюда
, отсюда
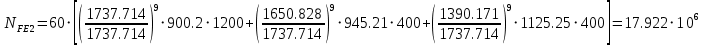
для шестерни «а»:
 ;
; 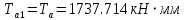 ;
; 

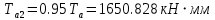 ;
; 

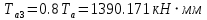 ;
; 
 , отсюда
, отсюда
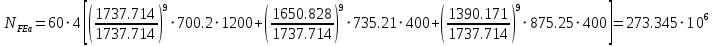
для сателлита «g»:
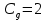 ;
;  ;
; 

 ;
; 

 ;
; 
 , отсюда
, отсюда
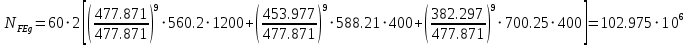
для корончатого колеса «b»:
 ;
;  ;
; 

 ;
; 

 ;
; 
 , отсюда
, отсюда
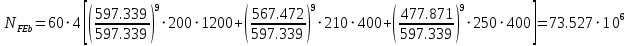
Допускаемые напряжения:
Т.к.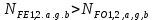 , то
, то 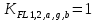 .
.
Т.к. зубья колес 1, 2, шестерни «а» и корончатого колеса «b» работают
одной стороной, то согласно рекомендации [1] имеем: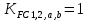 .
.
Т.к. зубья сателлита «» работают двумя сторонами, то согласно
рекомендации [1] имеем: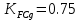 . Тогда допускаемые напряжения
. Тогда допускаемые напряжения
будут равны:
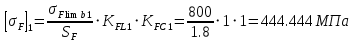 ,
,
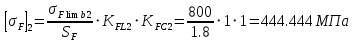 ,
,
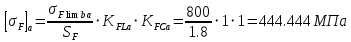 ,
,
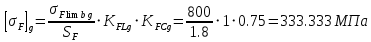 ,
,
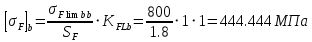
.
2.4 Расчёт цилиндрической передачи
2.4.1 Расчет основных параметров цилиндрической зубчатой передачи
с прямым зубом
Из предыдущих расчётов:
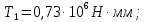
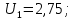
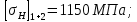
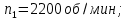
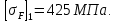
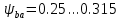 (согласно рекомендации [1]) - коэффициент ширины колеса относительно межосевого расстояния.
(согласно рекомендации [1]) - коэффициент ширины колеса относительно межосевого расстояния.
Примем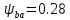 .
.
Коэффициент нагрузки: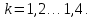
Принимаем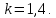
Определим межцентровое расстояние:
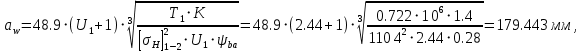 Тогда
Тогда 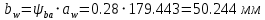 .
.
Округлив до целого значения, получим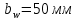 .
.
Увеличим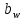 до 54 мм, чтобы обеспечить контактную прочность:
до 54 мм, чтобы обеспечить контактную прочность: 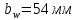 .
.
Примем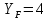 , (принимаем степень точности 7).
, (принимаем степень точности 7).
Определим модуль:
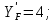
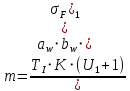 .
.
Округлим до ближайшего по ГОСТ 9563-60 (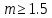 ), получим
), получим 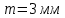 .
.
Определим число зубьев первой шестерни:
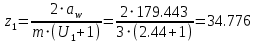 .
.
Округлив до целого значения, получим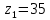 .
.
Определим число зубьев второй шестерни:
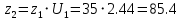 .
.
Округлив до целого значения, получим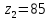 .
.
Вычислим передаточное число по формуле: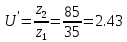
.
Вычислим ошибку: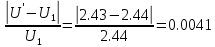 .
.
Согласно рекомендации [1]:
если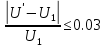 , тогда вычислим значение делительного диаметра шестерни по формуле:
, тогда вычислим значение делительного диаметра шестерни по формуле:
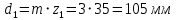 .
.
Определим окружную скорость:
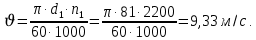
Определим новый коэффициент ширины зубчатого колеса относительно диаметра:
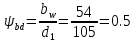 .
.
Коэффициент динамической нагрузки примем равным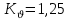 .
.
Коэффициент неравномерности нагрузки примем равным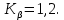 (симметричное расположение подшипников).
(симметричное расположение подшипников).
Тогда новый коэффициент нагрузки:
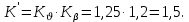
Коэффициент, учитывающий механические свойства материала, примем равным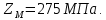
Коэффициент, учитывающий форму (геометрию) сопряженных профилей (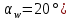 :
:
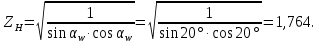
Определим действительное контактное напряжение в передаче:
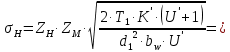
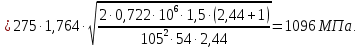
Тогда погрешность составит:
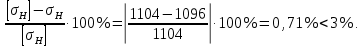
2.4.2 Расчёт цилиндрической прямозубой не корригированной передачи на изгибную прочность
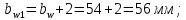
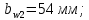
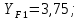
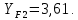
Определим действительное напряжение при изгибе в передаче:
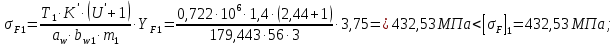
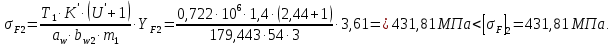
2.4.3 Определение геометрических параметров прямозубой цилиндрической передачи
Определяем делительное межосевое расстояние:
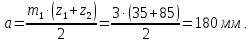
Тогда межосевое расстояние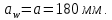
Определим делительный диаметр:
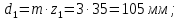
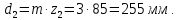
Определим начальный диаметр:
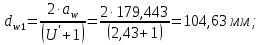
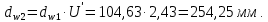
Определим диаметр вершин зубьев:
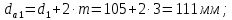
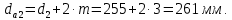
Определим диаметр впадин:
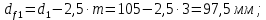
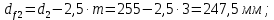
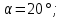
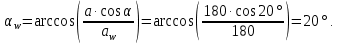
2.5 Расчёт планетарной передачи
2.5.1 Расчет параметров планетарной зубчатой передачи с прямым зубом
Из предыдущих расчётов:
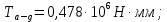
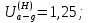
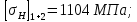

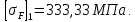
Коэффициент ширины зубчатого венца относительно межцентрового расстояния: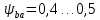 (колёса расположены симметрично относительно опор).
(колёса расположены симметрично относительно опор).
Принимаем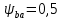 .
.
Коэффициент нагрузки:
Принимаем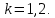
Определим межцентровое расстояние:
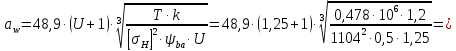
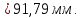
Определим ширину зубчатого колеса:
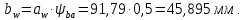
Принимаем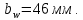
Примем , (т.к. степень точности 7).
, (т.к. степень точности 7).
Определим модуль:


 ;
; 
 , отсюда
, отсюда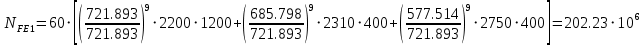
для колеса
 :
: ;
;  ;
; 

 ;
; 

 ;
; 
 , отсюда
, отсюда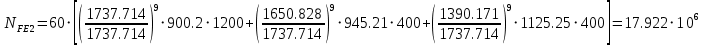
для шестерни «а»:
 ;
; 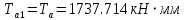 ;
; 

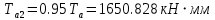 ;
; 

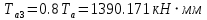 ;
; 
 , отсюда
, отсюда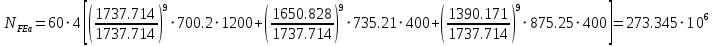
для сателлита «g»:
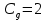 ;
;  ;
; 

 ;
; 

 ;
; 
 , отсюда
, отсюда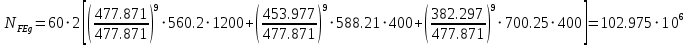
для корончатого колеса «b»:
 ;
;  ;
; 

 ;
; 

 ;
; 
 , отсюда
, отсюда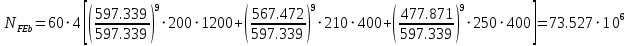
Допускаемые напряжения:
Т.к.
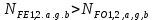 , то
, то 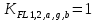 .
.Т.к. зубья колес 1, 2, шестерни «а» и корончатого колеса «b» работают
одной стороной, то согласно рекомендации [1] имеем:
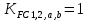 .
. Т.к. зубья сателлита «» работают двумя сторонами, то согласно
рекомендации [1] имеем:
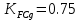 . Тогда допускаемые напряжения
. Тогда допускаемые напряжениябудут равны:
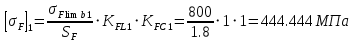 ,
,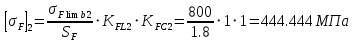 ,
,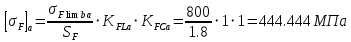 ,
,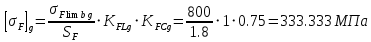 ,
,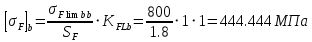
.
2.4 Расчёт цилиндрической передачи
2.4.1 Расчет основных параметров цилиндрической зубчатой передачи
с прямым зубом
Из предыдущих расчётов:
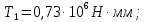
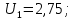
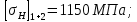
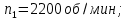
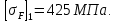
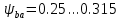 (согласно рекомендации [1]) - коэффициент ширины колеса относительно межосевого расстояния.
(согласно рекомендации [1]) - коэффициент ширины колеса относительно межосевого расстояния.Примем
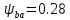 .
.Коэффициент нагрузки:
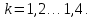
Принимаем
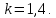
Определим межцентровое расстояние:
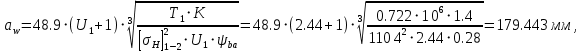 Тогда
Тогда 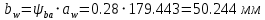 .
. Округлив до целого значения, получим
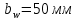 .
.Увеличим
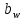 до 54 мм, чтобы обеспечить контактную прочность:
до 54 мм, чтобы обеспечить контактную прочность: 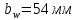 .
.Примем
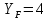 , (принимаем степень точности 7).
, (принимаем степень точности 7).Определим модуль:
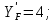
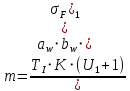 .
.Округлим до ближайшего по ГОСТ 9563-60 (
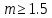 ), получим
), получим 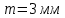 .
.Определим число зубьев первой шестерни:
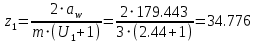 .
.Округлив до целого значения, получим
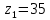 .
.Определим число зубьев второй шестерни:
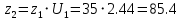 .
. Округлив до целого значения, получим
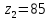 .
.Вычислим передаточное число по формуле:
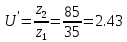
.
Вычислим ошибку:
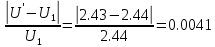 .
.Согласно рекомендации [1]:
если
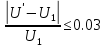 , тогда вычислим значение делительного диаметра шестерни по формуле:
, тогда вычислим значение делительного диаметра шестерни по формуле: 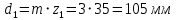 .
.Определим окружную скорость:
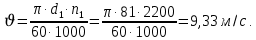
Определим новый коэффициент ширины зубчатого колеса относительно диаметра:
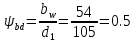 .
.Коэффициент динамической нагрузки примем равным
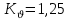 .
.Коэффициент неравномерности нагрузки примем равным
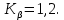 (симметричное расположение подшипников).
(симметричное расположение подшипников).Тогда новый коэффициент нагрузки:
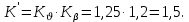
Коэффициент, учитывающий механические свойства материала, примем равным
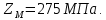
Коэффициент, учитывающий форму (геометрию) сопряженных профилей (
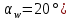 :
: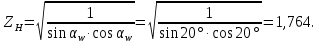
Определим действительное контактное напряжение в передаче:
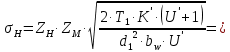
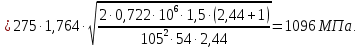
Тогда погрешность составит:
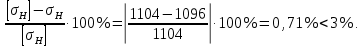
2.4.2 Расчёт цилиндрической прямозубой не корригированной передачи на изгибную прочность
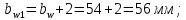
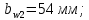
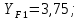
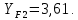
Определим действительное напряжение при изгибе в передаче:
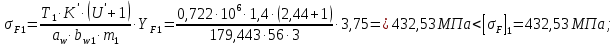
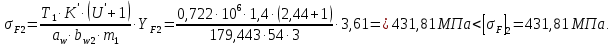
2.4.3 Определение геометрических параметров прямозубой цилиндрической передачи
Определяем делительное межосевое расстояние:
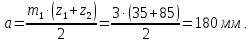
Тогда межосевое расстояние
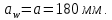
Определим делительный диаметр:
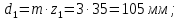
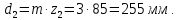
Определим начальный диаметр:
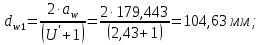
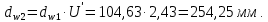
Определим диаметр вершин зубьев:
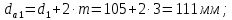
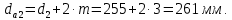
Определим диаметр впадин:
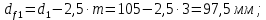
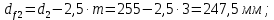
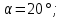
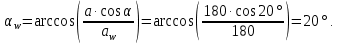
2.5 Расчёт планетарной передачи
2.5.1 Расчет параметров планетарной зубчатой передачи с прямым зубом
Из предыдущих расчётов:
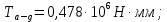
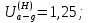
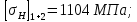

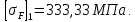
Коэффициент ширины зубчатого венца относительно межцентрового расстояния:
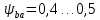 (колёса расположены симметрично относительно опор).
(колёса расположены симметрично относительно опор).Принимаем
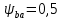 .
.Коэффициент нагрузки:

Принимаем
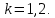
Определим межцентровое расстояние:
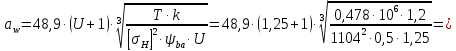
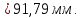
Определим ширину зубчатого колеса:
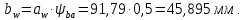
Принимаем
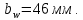
Примем
 , (т.к. степень точности 7).
, (т.к. степень точности 7).Определим модуль: