ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 99
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 3
3.1. Найти единичный вектор
, перпендикулярный вектору 
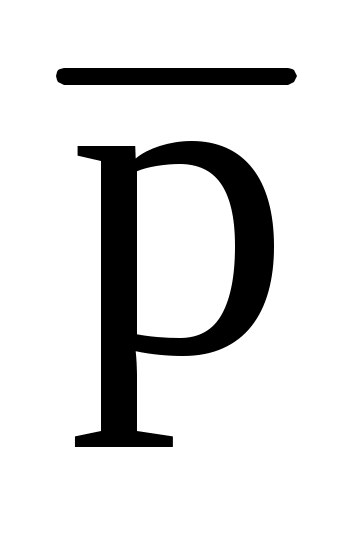
(3; -2; 1) и к оси Oy.3.2. В плоскости Oxz найти вектор
, перпендикулярный вектору 
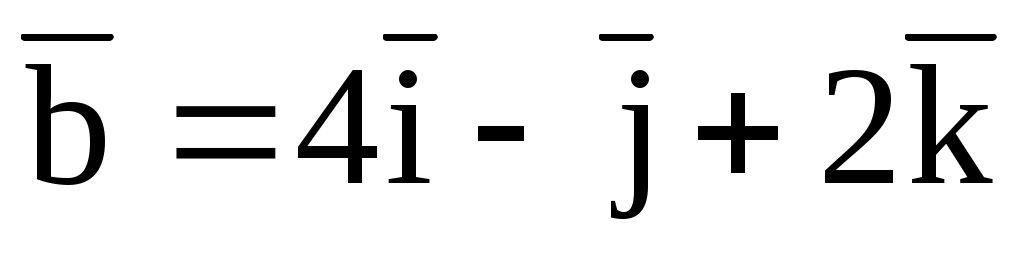
, длина которого равна 3
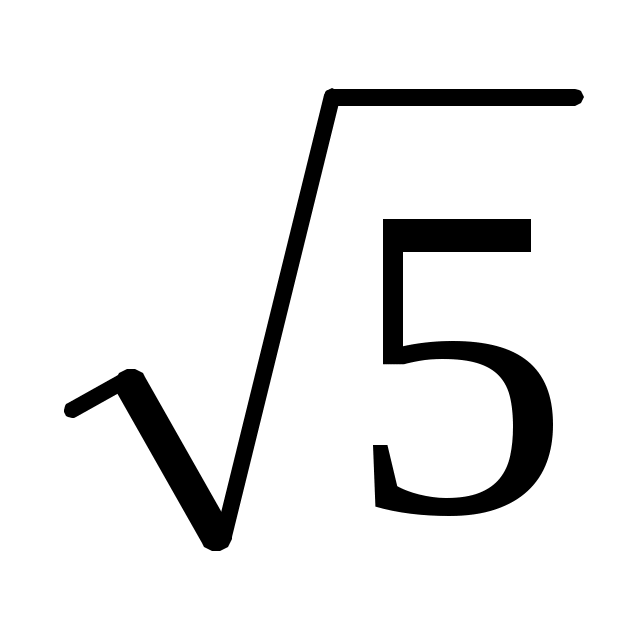
.3.3. В плоскости Oxz найти вектор
, перпендикулярный вектору 
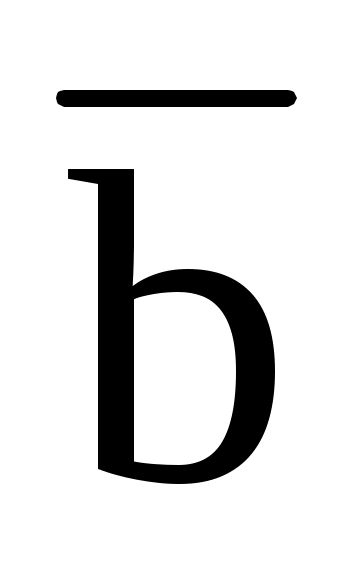
(-2; 4; 4) и имеющий одинаковую с ним длину.3.4. Вектор
, перпендикулярный к векторам (2; -1; 3) и 
(1; 1; 4), образует с осью Oz тупой угол. Найти его координаты, зная, что 
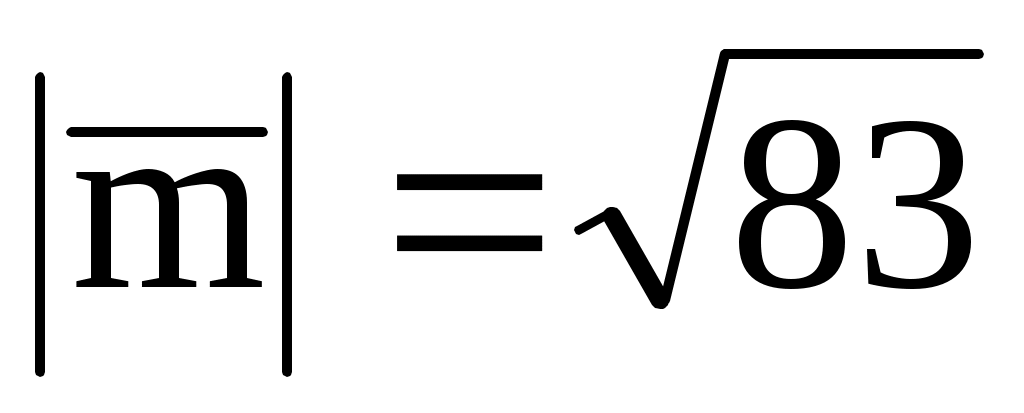
.3.5. Найти вектор
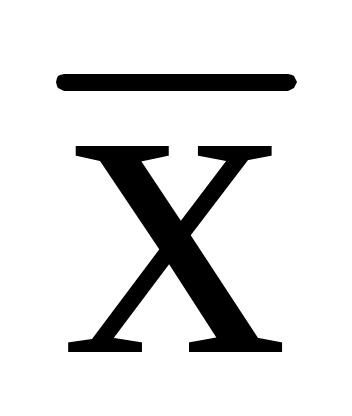
, зная, что он перпендикулярен векторам (2; -3; 1) и (1; -2; 3) и удовлетворяет условию: (
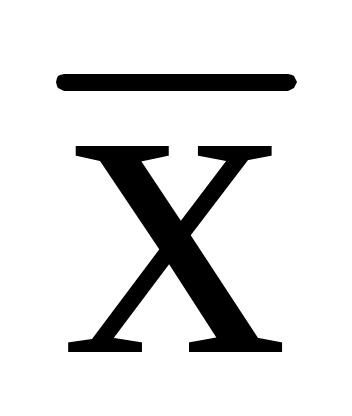
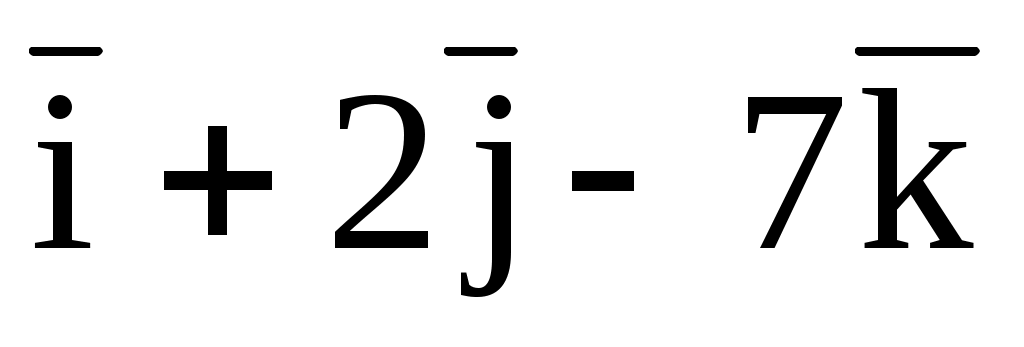
) = 10.3.6. Найти вектор
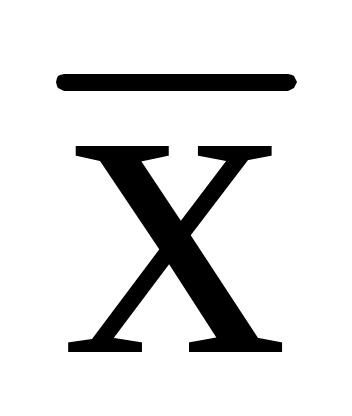
, перпендикулярный векторам 
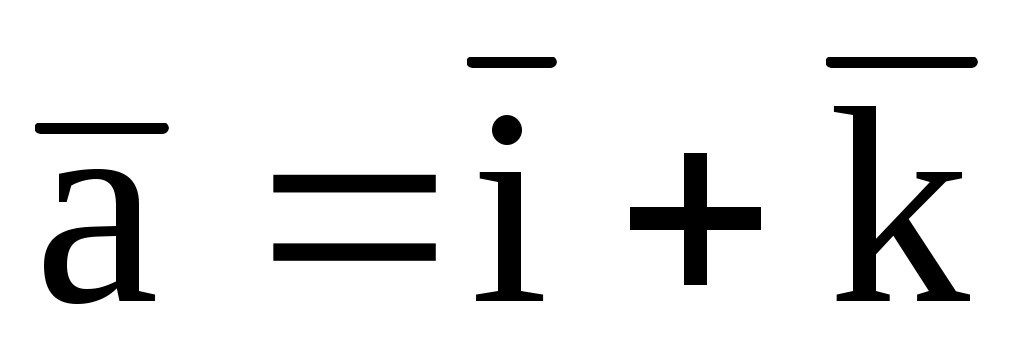
и 
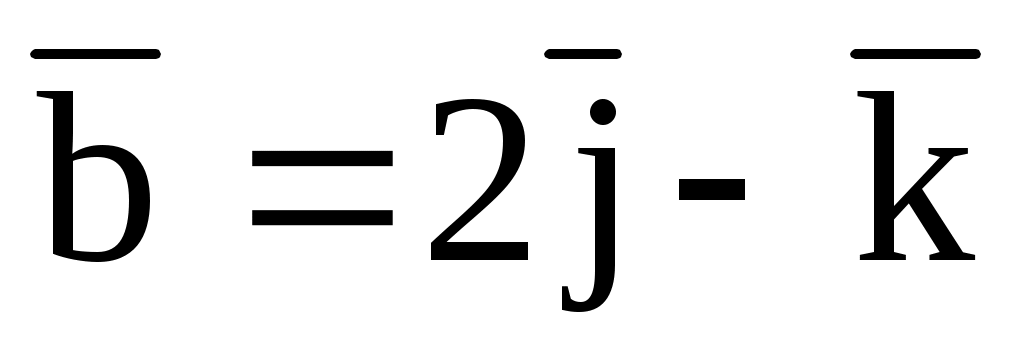
, если 
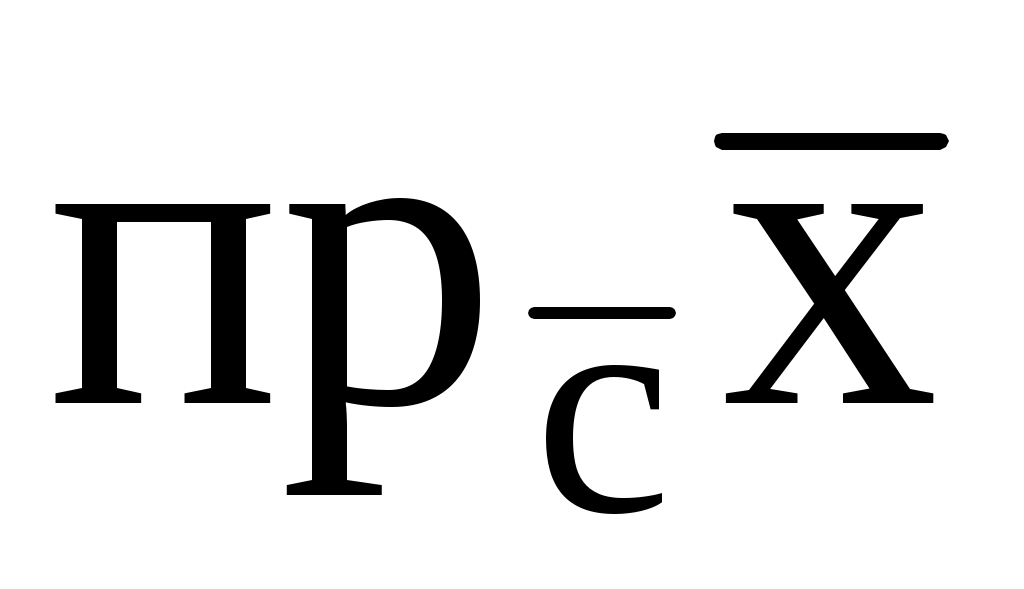
= 1, где 
(1; 2; 2).3.7. Даны два вектора:
(2; 0; -1) и
(0; -2; 0). Найти единичный вектор , перпендикулярный вектору и образующий с вектором угол 60.3.8. Найти вектор
, коллинеарный вектору (3; -2; -3), если 
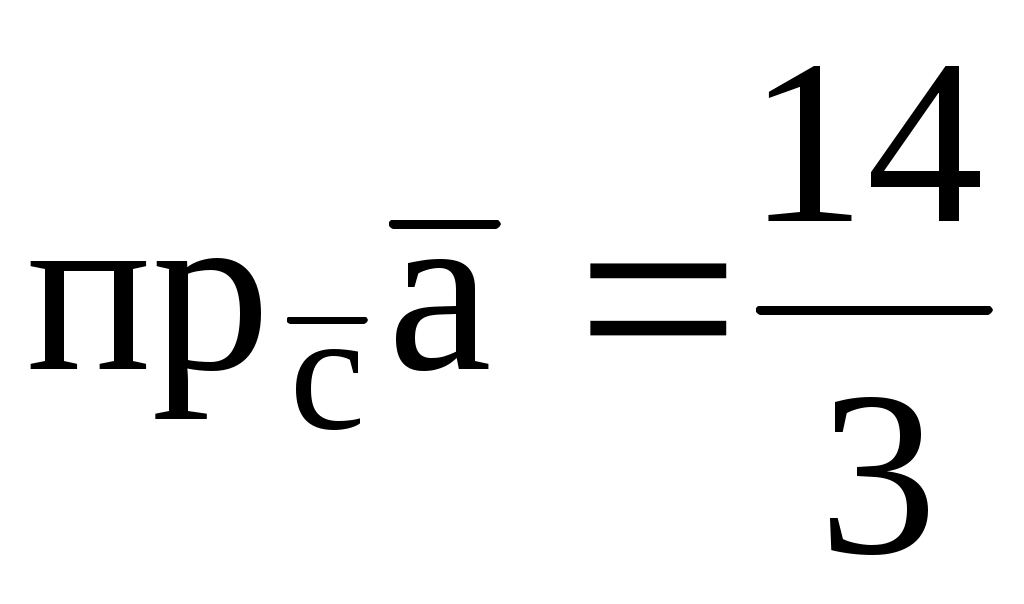
, где 
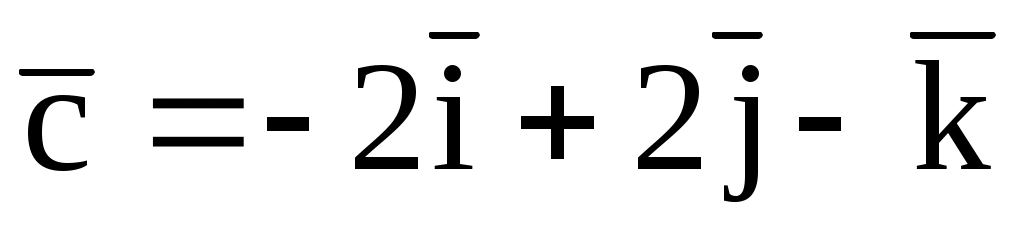
.3.9. Вектор
, перпендикулярный к оси Oy и к вектору (-1; 3; -5), образует тупой угол с осью Oz. Найти его координаты, если 
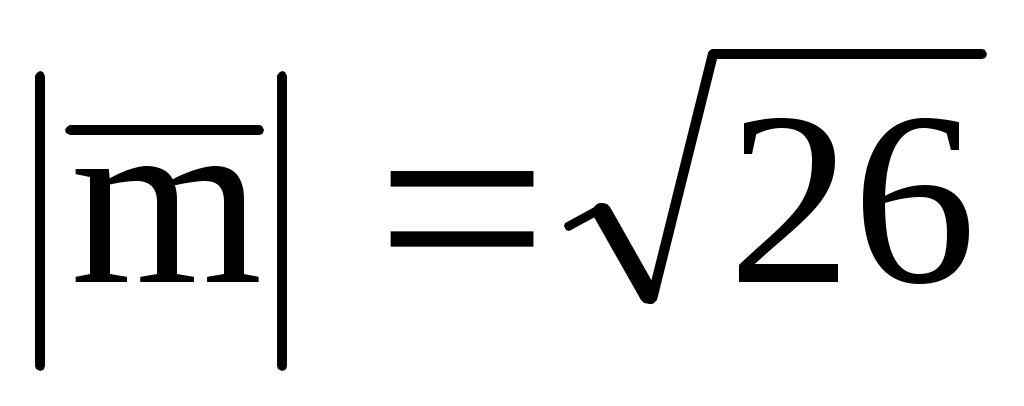
.3.10. Даны два вектора:
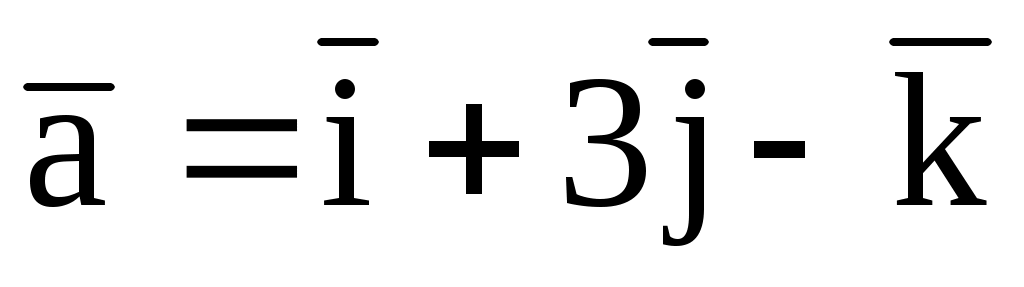
и 
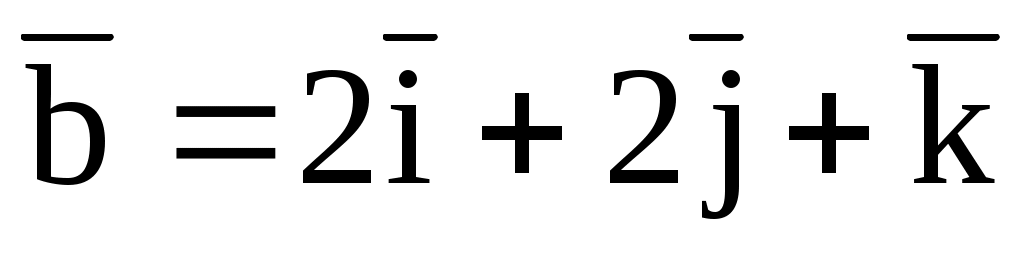
. Найти вектор 
, если 
; 
; 
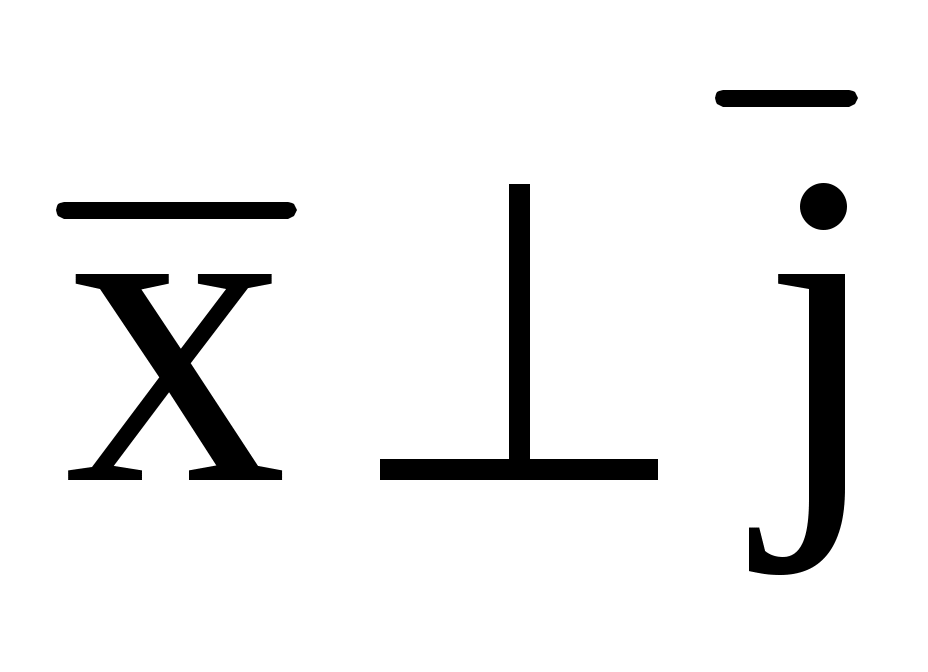
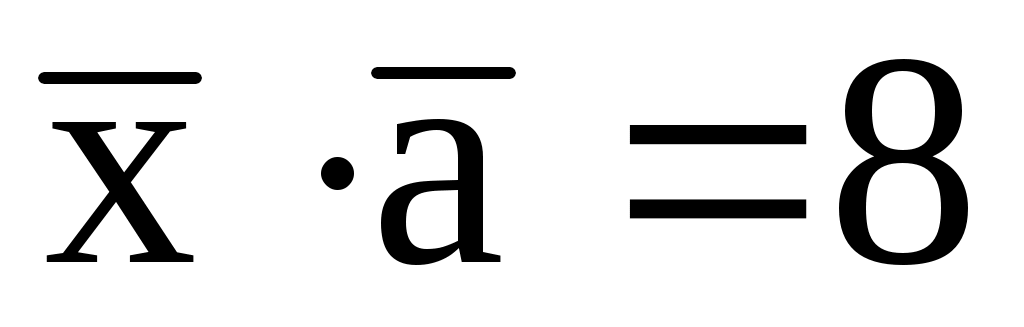
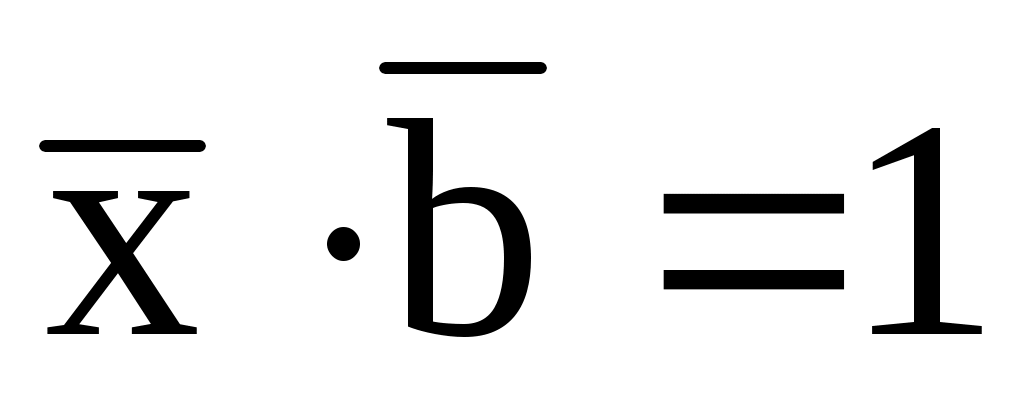
.3.11. Даны три силы
, 
, 
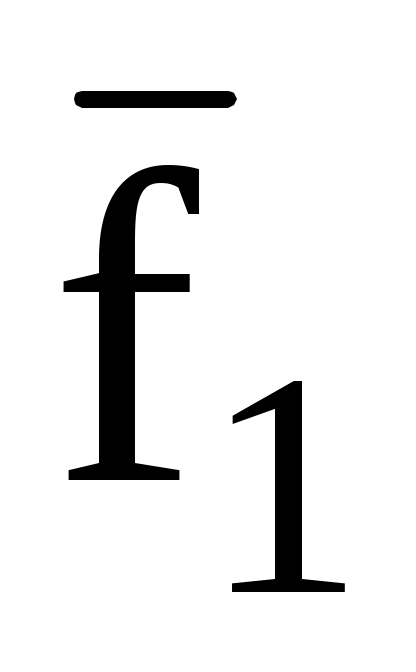
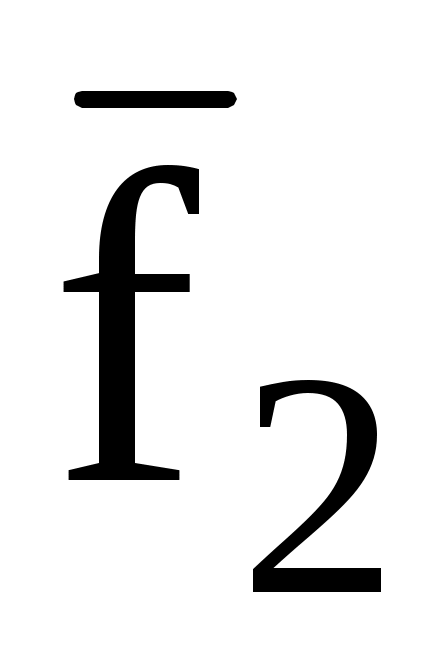
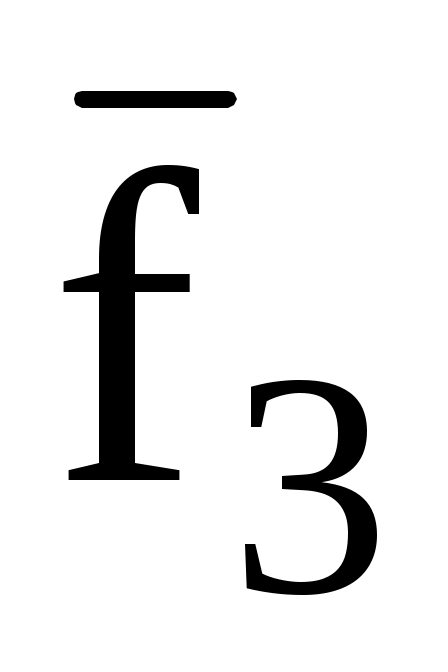
, приложенные к одной точке. Вычислить работу равнодействующей этих сил при перемещении точки из положения А в В, если:а)
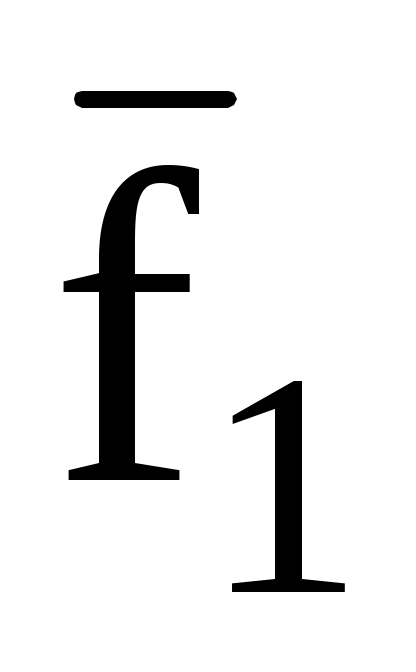
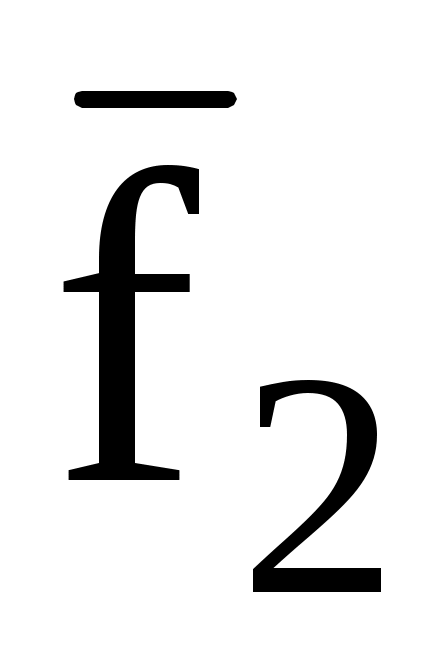
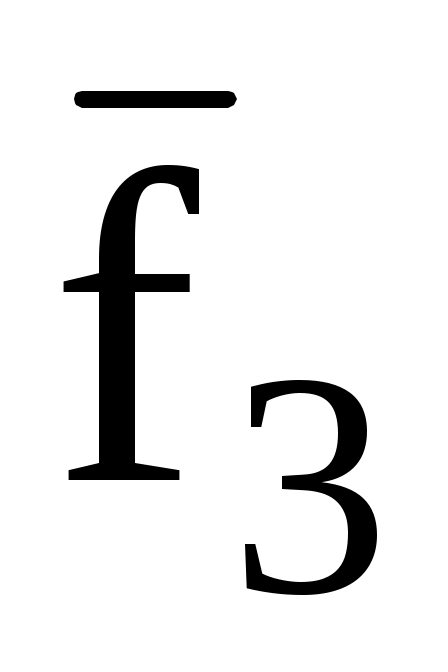
(3; -4; 2), (2; 3; -5), (-3; -2; 4), А(5; 3; -7), В(4; -1; -4).
б)
(2; -1; 1), 
(-1; 2; 2), 
(1; 1; -2), А(2; -1; 0), В(4; 1; -1).в)
(3; -4; 2), (2; 3; -5), (-3; -2; 4), А(0; 0; 0), В(1; 2; 1).г)
(3; 1; -2), (-1; 1; 3), (2; -5; 4), А(0; 2; -1), В(1; 1; -2).3.12. Даны три силы
, 
, 
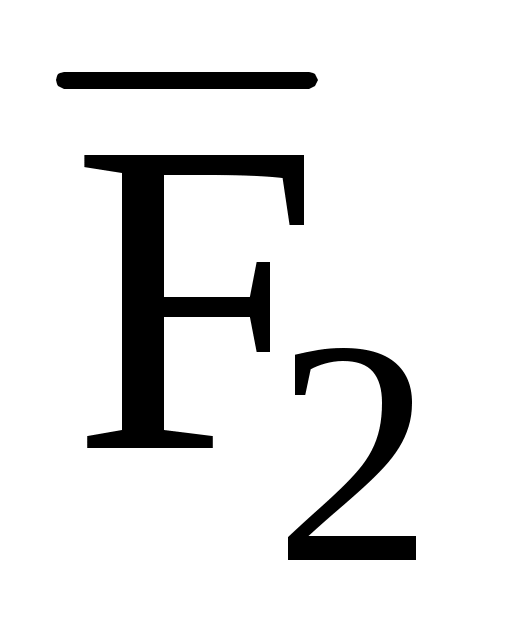
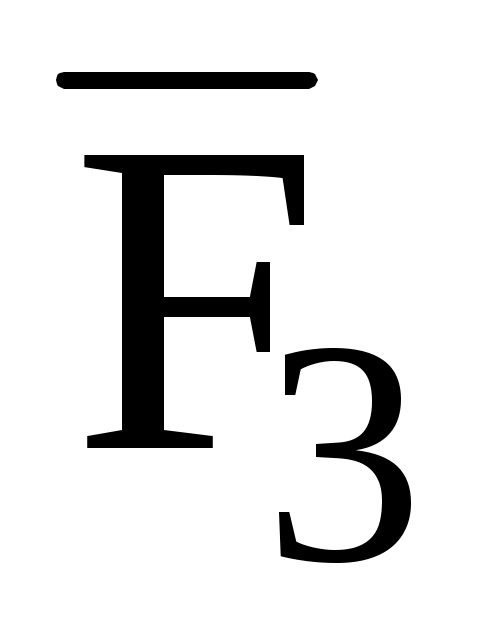
, приложенные к одной точке. При каком значении "m" работа равнодействующей этих сил при прямолинейном перемещении из положения А в положение В равна нулю, если:а)
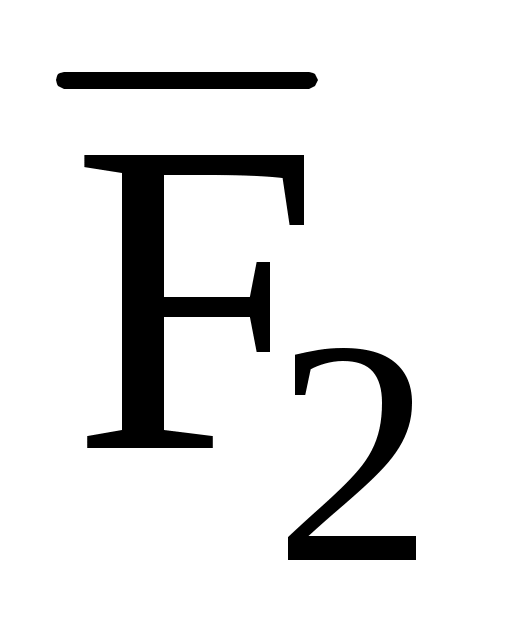
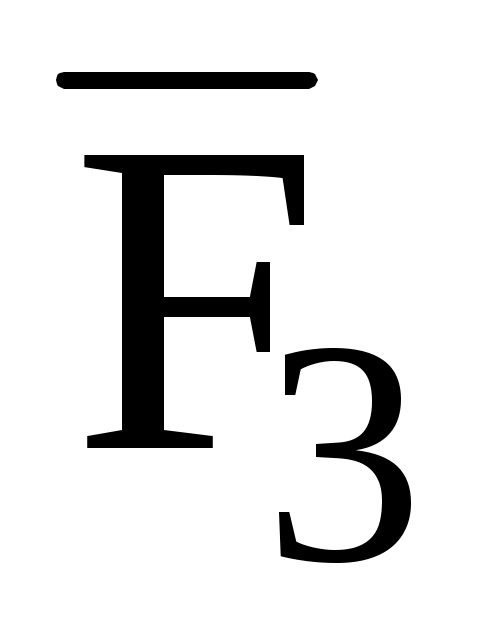
(3; -4; 2), (4; 5; m), (m; 0; -3), А(1; 2; -3), В(4; -1; 5);б)
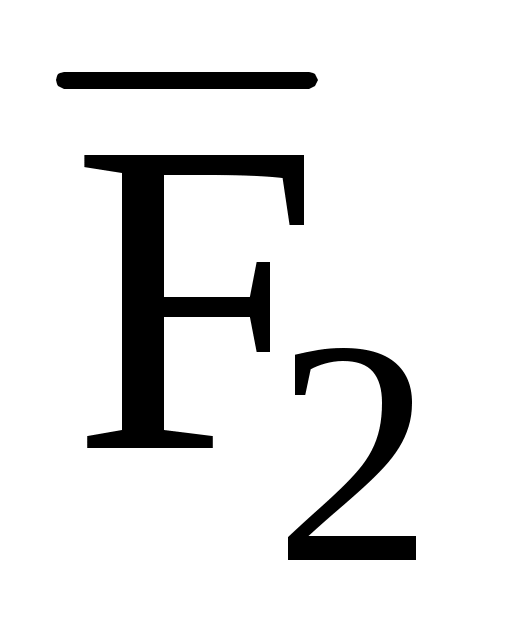
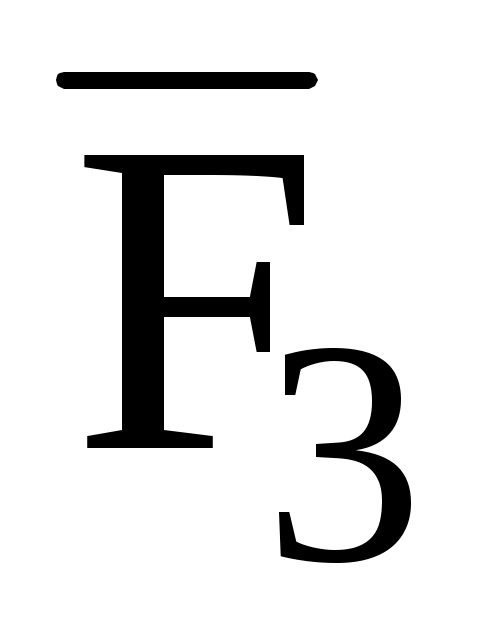
(m; -3; 1), (3; 4; 5), (1; m; -2), А(1; 2; -3), В(4; 0; 2);в)
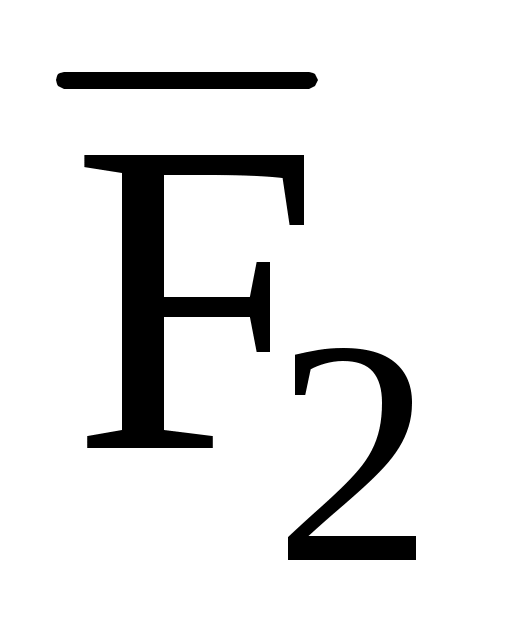
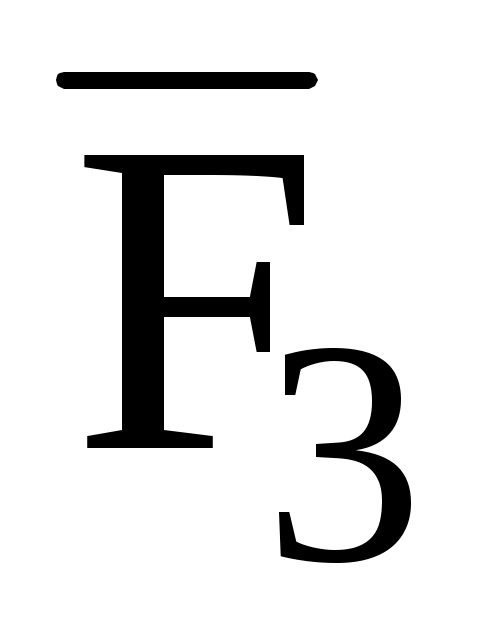
(5; -2; 4), (m; 2; -3), (2; m; 5), А(-1; 2; 3), В(4; -1; 8);г)
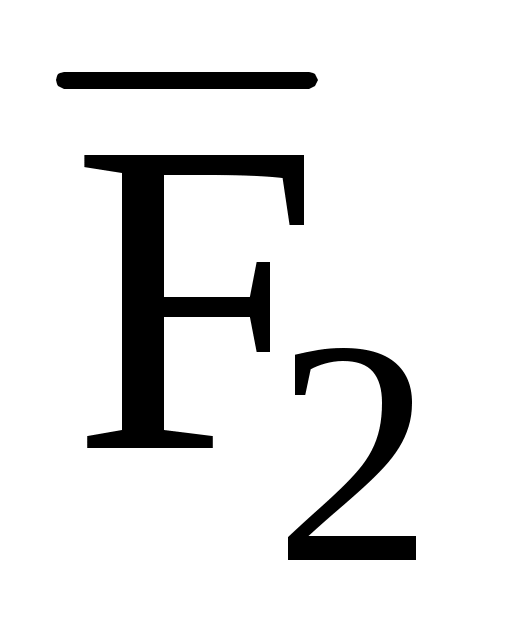
(3; 2; 1), (-1; m; 3),
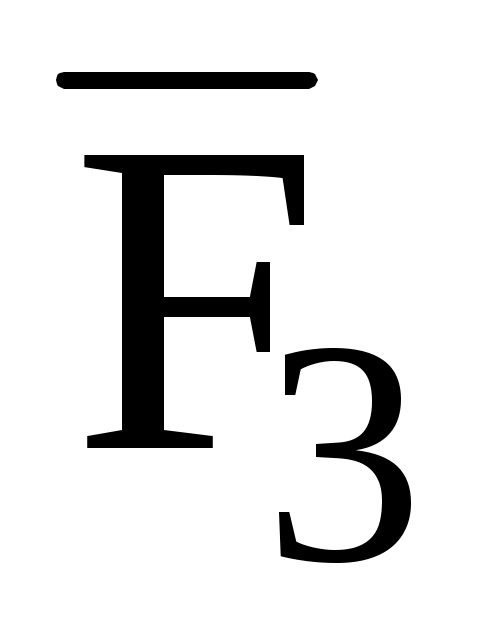
(2; 0; m), А(1; -3; 0), В(0; 2; -3).
3.13. Под действием силы
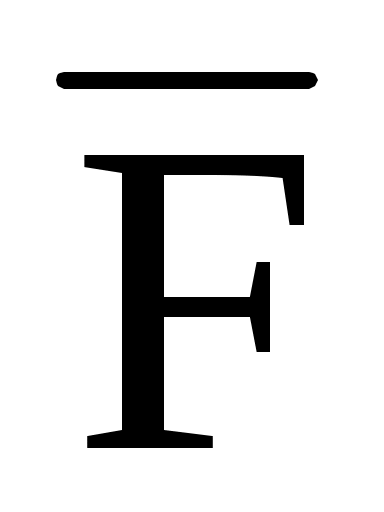
(2; 4; 6) точка переместилась на отрезок 
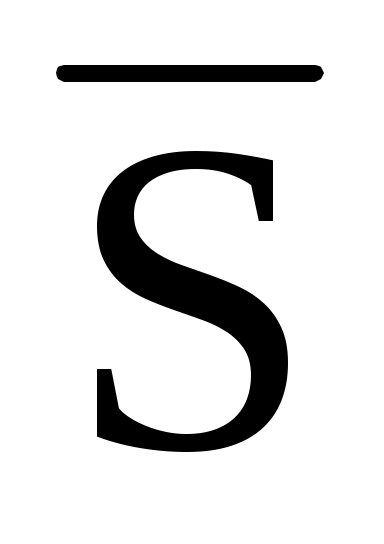
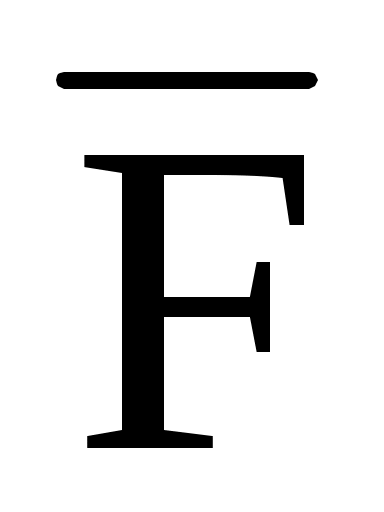
(3; 2; -1). Вычислить работу силы и угол (
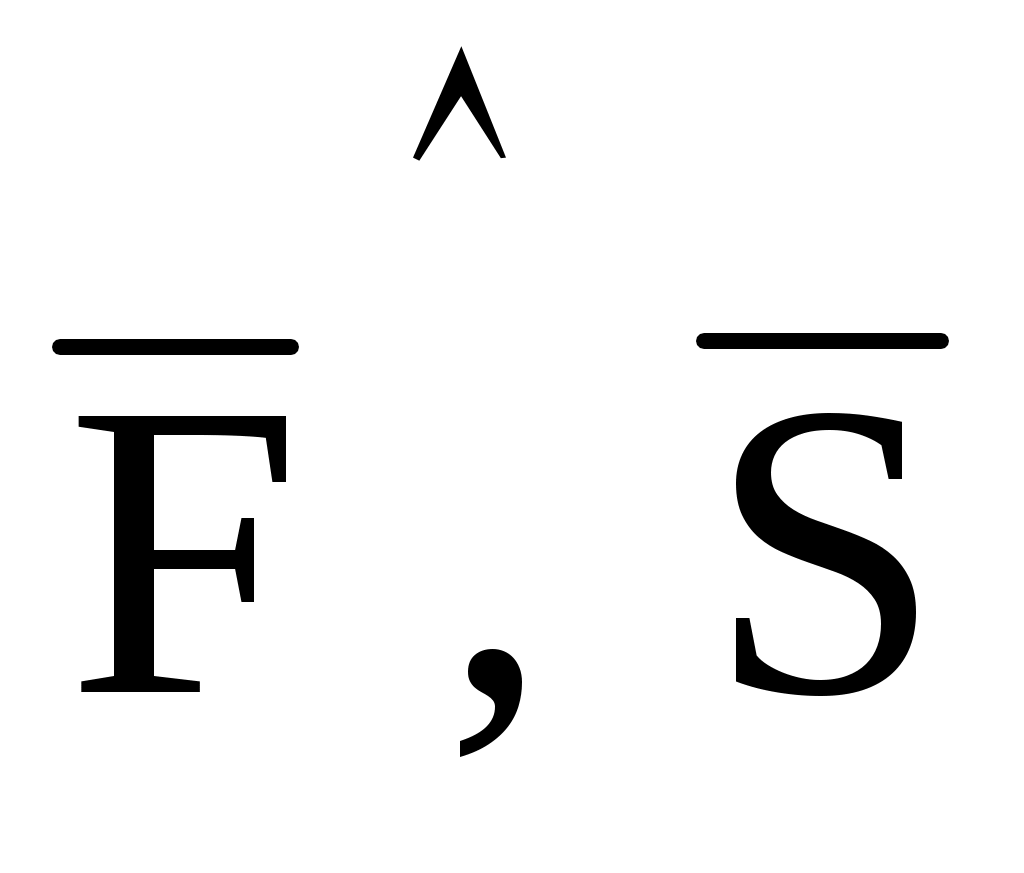
).3.14. Даны вершины 4-угольника ABCD. При каких значениях "u" его диагонали ортогональны, если:
а) А(-3;
; 6), В(-4; -1; 12), С(1; - ; 7), D(3; 1; 4);б) А(1; -5; 7), В(3; 1;
), С(-3; 5; 6), D(- ; -1; 12).3.15. Найти вектор
, коллинеарный вектору (2; -1; 3), если 
-42.3.16. В плоскости xOz найти вектор
, если 
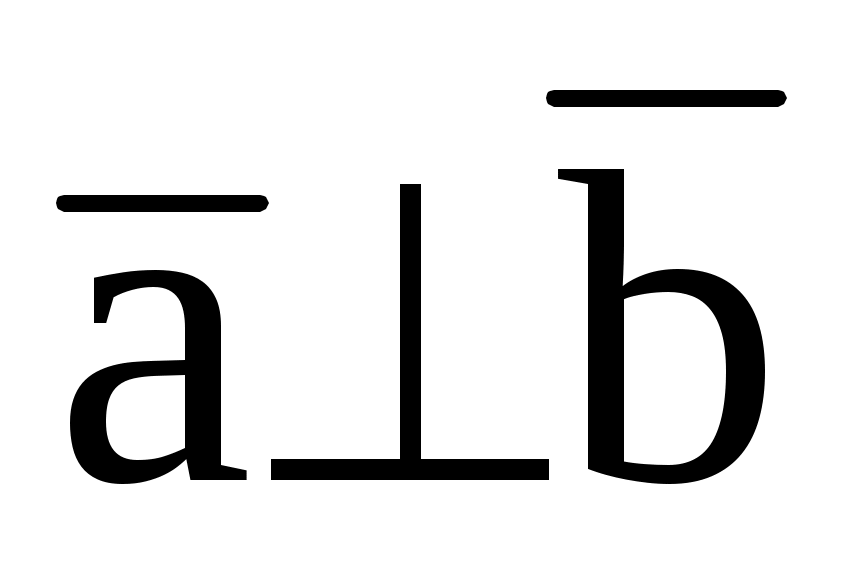
(-3; 5; -4) и 
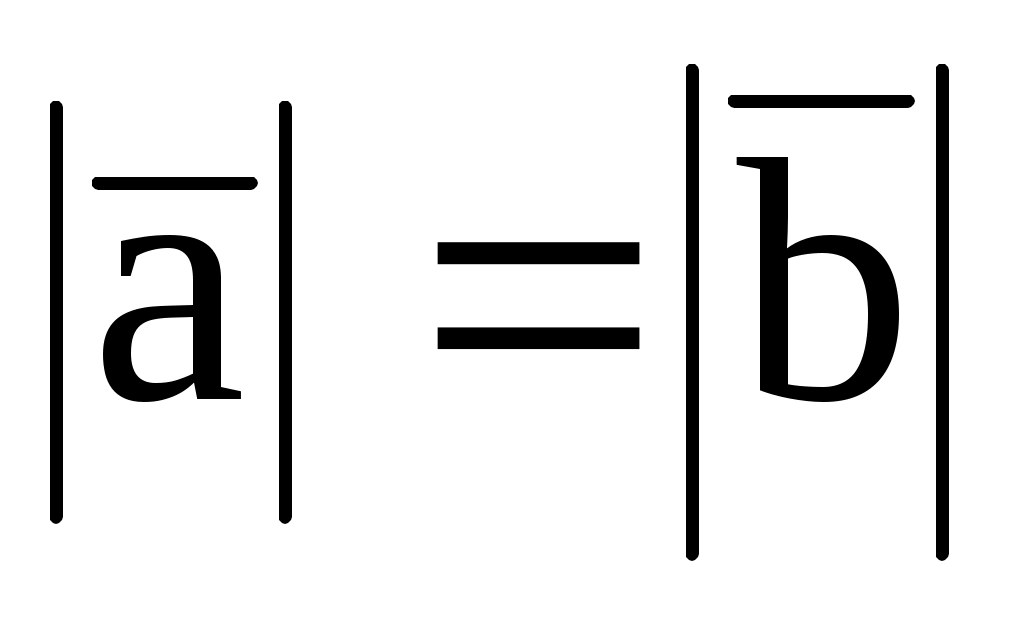
.3.17. В плоскости xOy найти вектор
, перпендикулярный вектору (3; 3; -1), если 
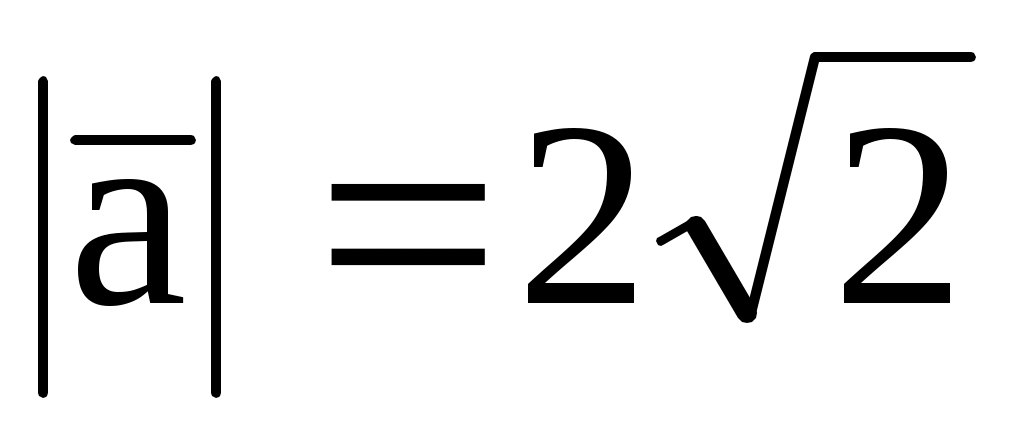
.3.18. Найти единичный вектор
, перпендикулярный вектору (1; -2; 3) и к оси Oz.3.19. Найти вектор
, зная, что он перпендикулярен векторам (1; 1; 2) и
(-2; 2; 3) и удовлетворяет условию
.3.20. Найти вектор
, перпендикулярный векторам (2; -1; 3) и (1; 1; 1), если 
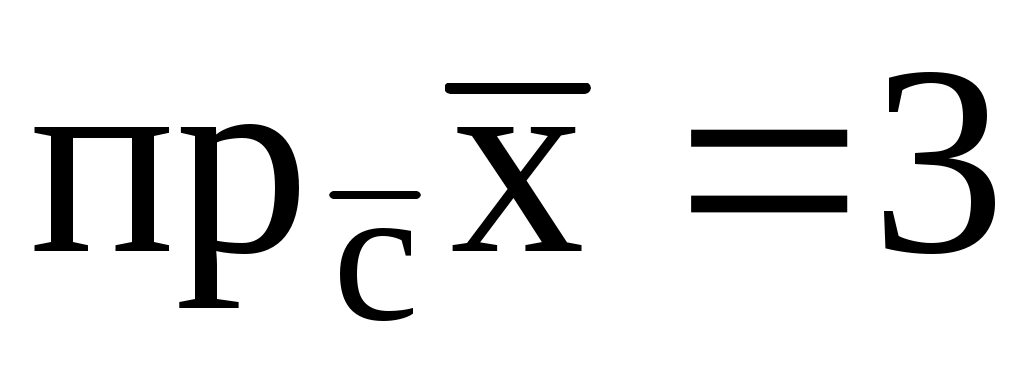
, где (2; 2; -1).3.21. Найти вектор
, коллинеарный вектору (1; -1; 3), если 
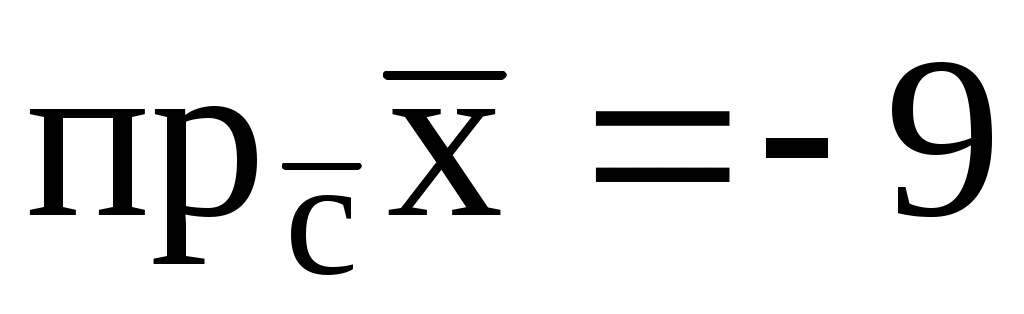
, где 
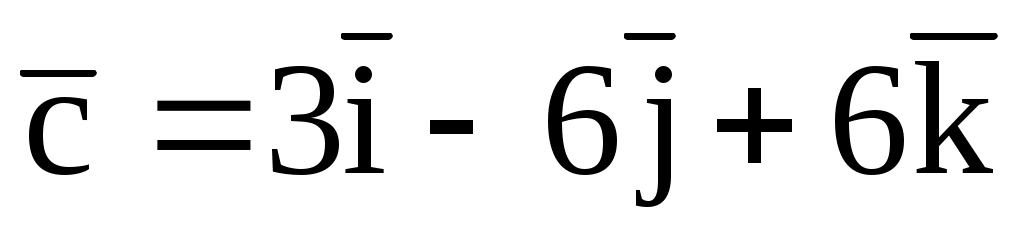
.3.22. Даны три вектора:
, 
, 
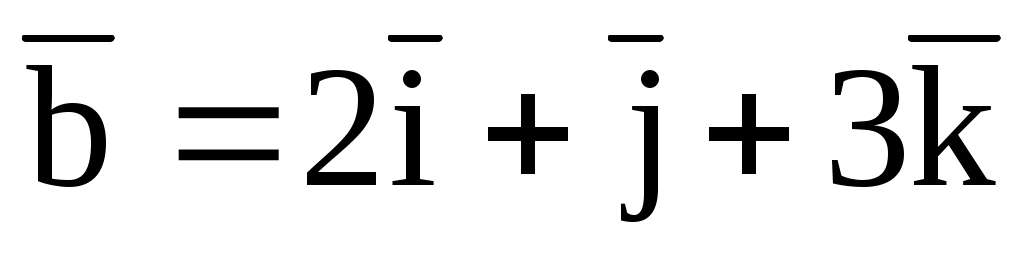
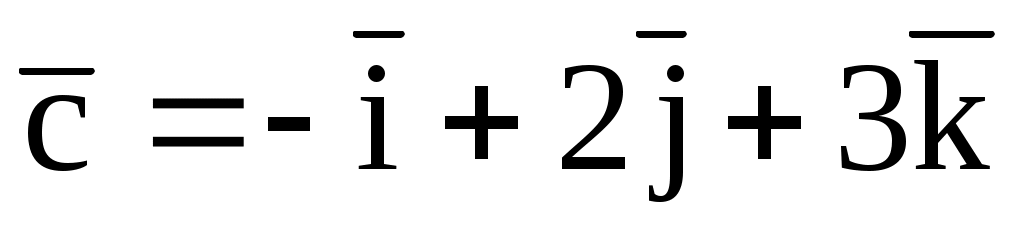
. Найти вектор , удовлетворяющий условиям: 
, 
, 
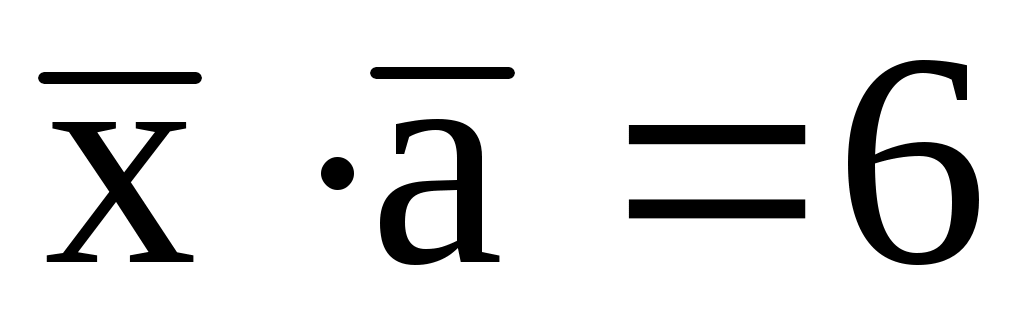
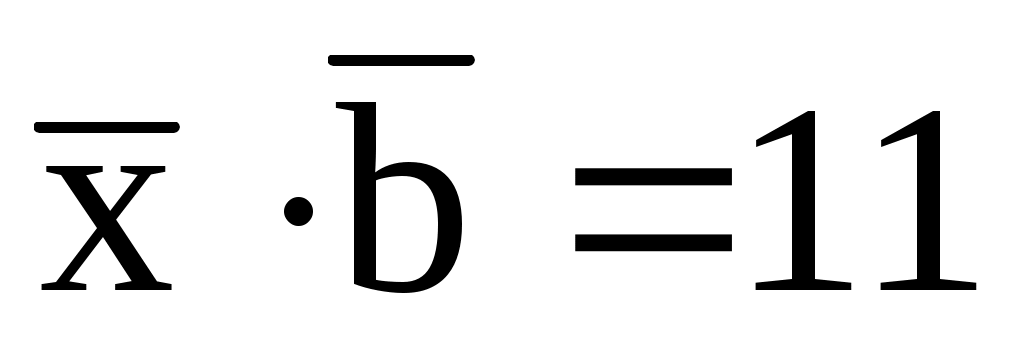
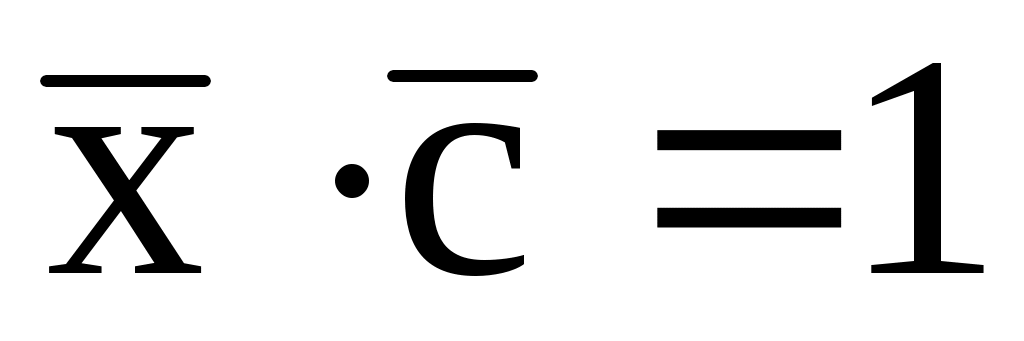
.3.23. Даны два вектора:
= (2; 2; 1) и = (1; -3; -4). Найти вектор при условии, что он перпендикулярен оси Ox и удовлетворяет условиям: 
, 
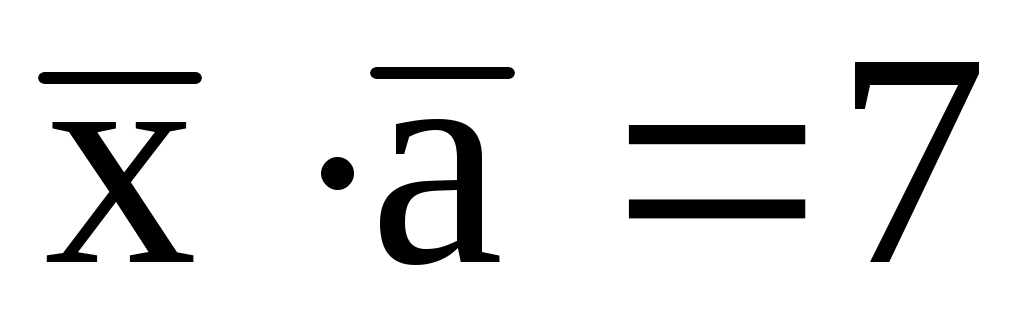
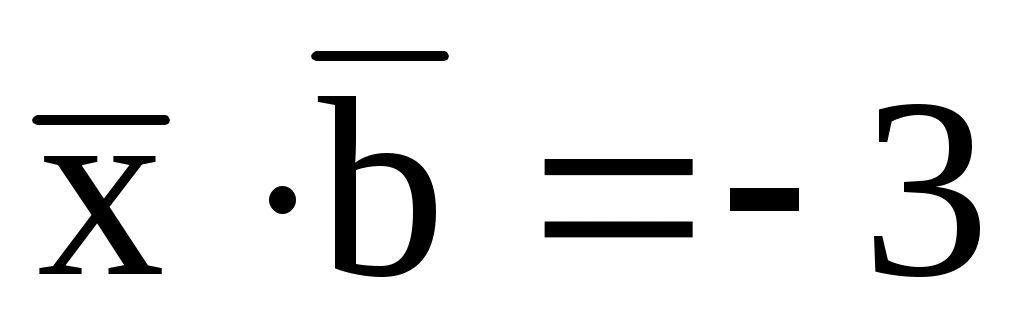
.Задание 4
Упростить выражение, задающее вектор
, найти модуль вектора