ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 103
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= (-3; 1; 2),  = (1; 2; 3). Вычислить
= (1; 2; 3). Вычислить 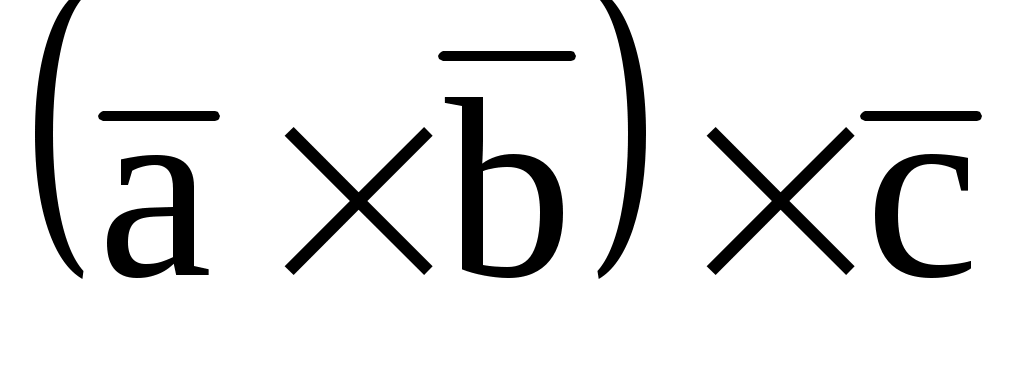 и
и 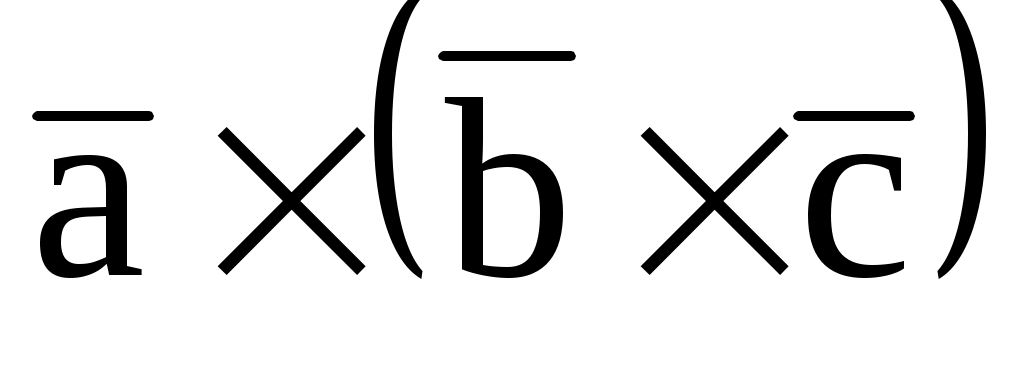 .
.
7.5. Даны точки A, B, C, D. При каком значении "t" тройка векторов ,
,  ,
,  будет:
будет:
а) левой, если А(1; -2; 0), В(3; t; -2), С(0; 1; 5), D(2; 2; -1);
б) правой, если А(3; -1; 2), В(2; 2; 0), С(2t; 1; 3), D(0; -1; 3).
7.6. Проверить, лежат ли в одной плоскости точки A, B, C, и D:
а) А(-1; 2; 1), В(0; 1; -2), С(1; 3; -2) и D(2; 4; -3);
б) А(-1; 2; 1), В(-7; 0; -3), С(4; -1; 2) и D(-2; 1; 0).
7.7. При каком значении t точки A, B, C, и D лежат в одной плоскости, если:
а) А(2; 0; -1), В(1; 1; 0), С(0; -1; t) и D(-1; 2; 2);
б) А(-1; 3; 2), В(2t; -1; 1), С(t; 2; 0) и D(1; 1; 1).
7.8. При каком значении t компланарны векторы ,
,  и
и 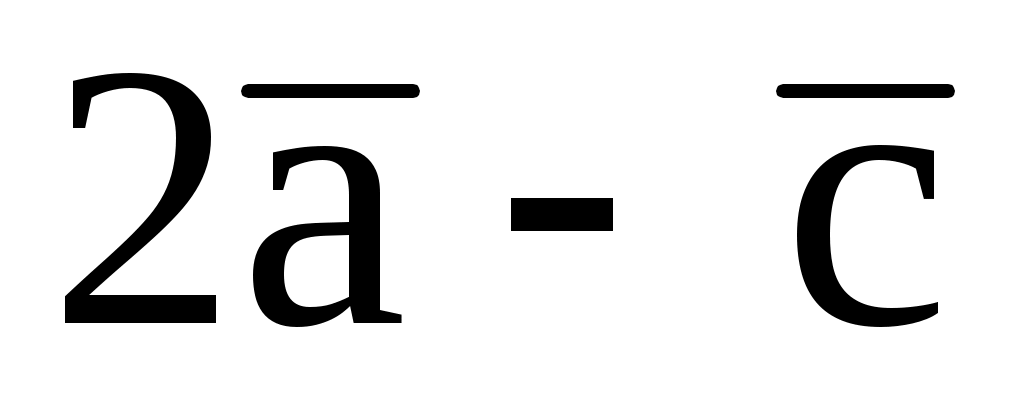 , если:
, если:
а) = (2; 1; -1),
= (2; 1; -1),  (1; 2t; -1),
(1; 2t; -1), 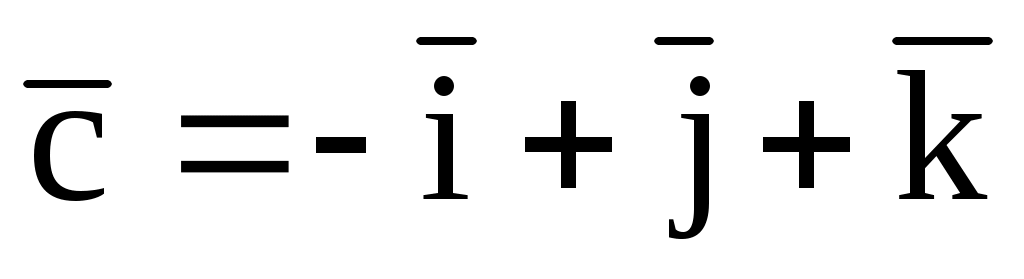 ;
;
б) ,
,  (1; 1; 0),
(1; 1; 0), 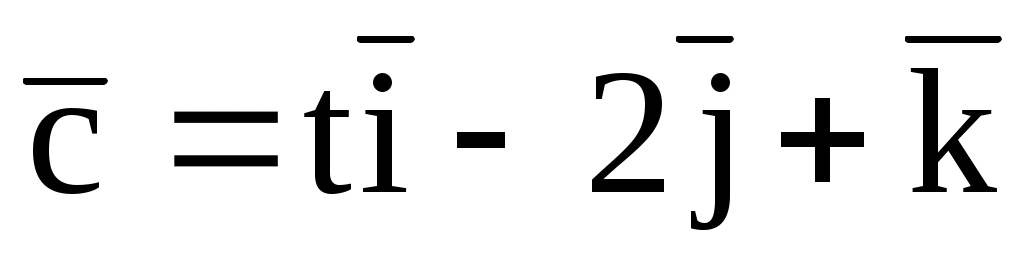 .
.
7.9. Найти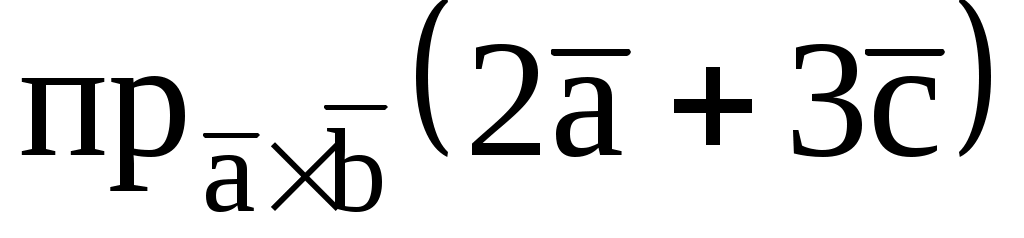 , если
, если  = (1; 1; -1),
= (1; 1; -1), 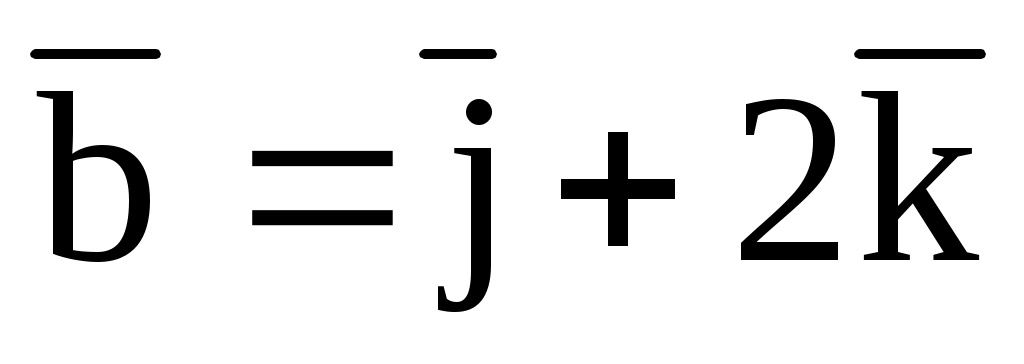 ,
,  = (-1; 0; 1).
= (-1; 0; 1).
7.10. Найти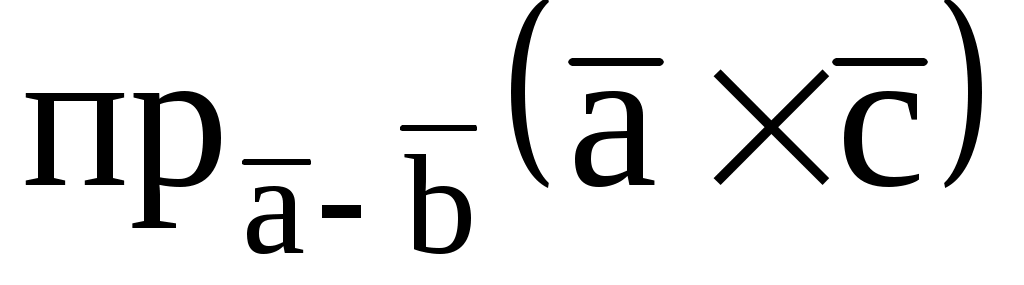 , если
, если 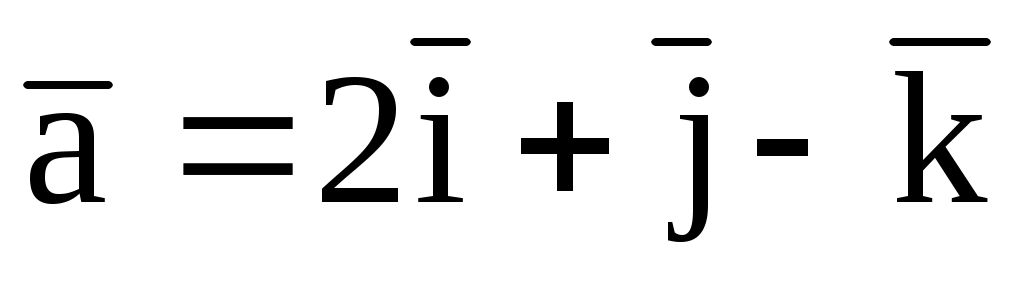
, = (1; 2; 3),
= (1; 2; 3),  = (-1; 0; 2).
= (-1; 0; 2).
7.11. При каком значении m векторы (1; m; -1),
(1; m; -1),  (2; 1; 3) и
(2; 1; 3) и  (-5; -1; 0) удовлетворяют соотношению
(-5; -1; 0) удовлетворяют соотношению 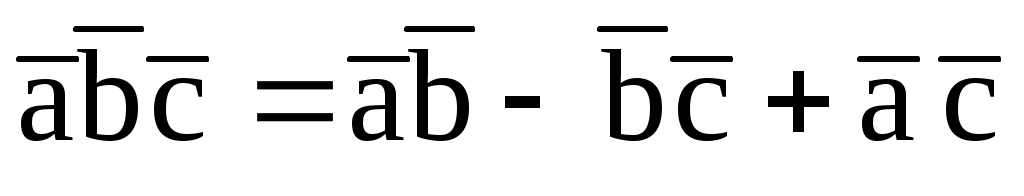 ?
?
7.12. Объём тетраэдра ABCD равен V. Найти координаты вершины D, если:
а) V = 2; А(2; 1; 3), В(3; 3; 2), С(1; 2; 4), DOz;
б) V = 3; А(1; 2; 3), В(3; 2; 1), С(2; 3; 1), DOx;
в) V = 5; А(2; 1; -1), В(3; 0; 1), С(2; -1; 3), DOy.
7.13. При каком значении m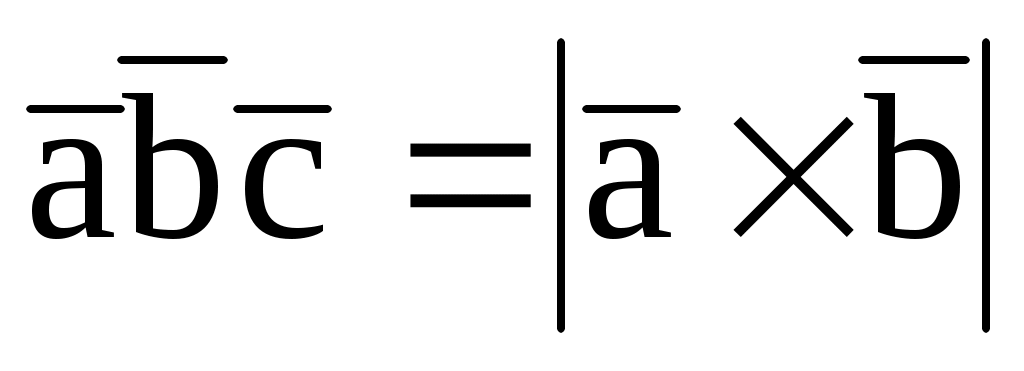 , если
, если  = (2; -2; -3),
= (2; -2; -3),  = (4; 0; 6),
= (4; 0; 6),  = (m; 1; -1).
= (m; 1; -1).
7.14. При каком значении m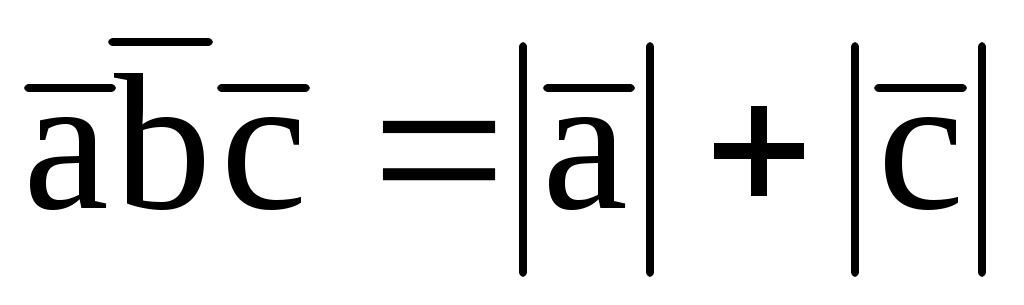 , если
, если  (1; 2; -2),
(1; 2; -2),  (m; -1; 1),
(m; -1; 1),
 (-6; 2; 6)
(-6; 2; 6)
7.15. При каком значении m тройка векторов (3; 1; -1),
(3; 1; -1),  (-1; m; 3),
(-1; m; 3),
 (2; 2; -2) будет левой и объём параллелепипеда, на них построенного, равен 8 ед3?
(2; 2; -2) будет левой и объём параллелепипеда, на них построенного, равен 8 ед3?
7.16. При каком значении m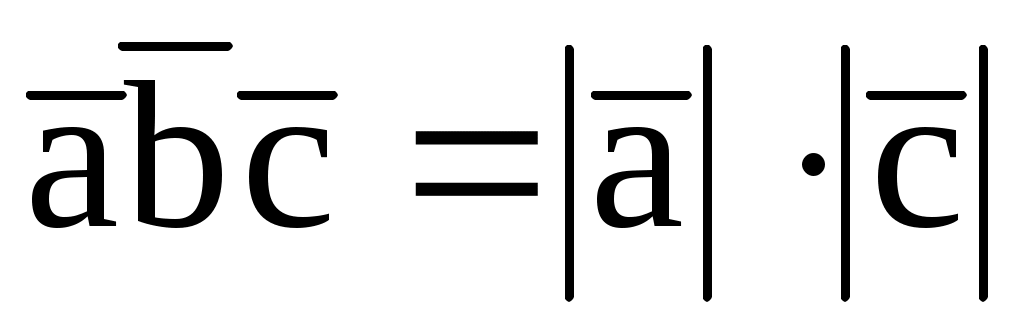 , если
, если  = (2; 2; -1),
= (2; 2; -1),  (-1; 3; m),
(-1; 3; m), 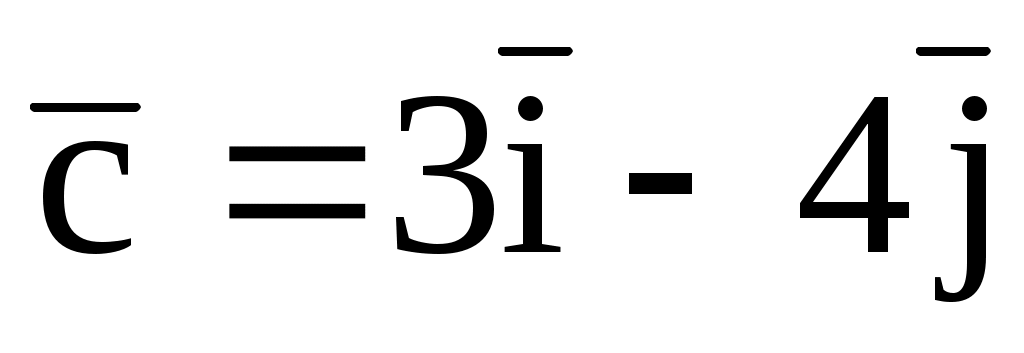 .
.
7.17. Векторы
(3; 3; -4) и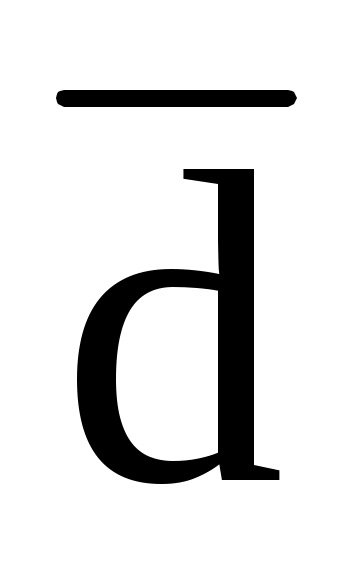 (-1; 1; 2) являются диагоналями параллелограмма, построенного на векторах
(-1; 1; 2) являются диагоналями параллелограмма, построенного на векторах  и
и  . Найти векторы
. Найти векторы  ,
,  и площадь параллелограмма.
и площадь параллелограмма.
7.18. Найти единичный вектор, параллельный вектору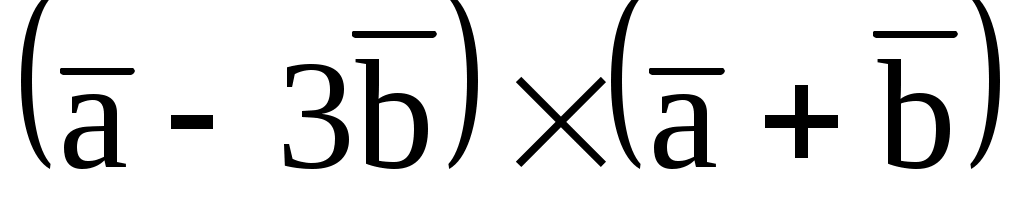 , если
, если  = (2; -1; 3),
= (2; -1; 3),  = (1; 1; 2).
= (1; 1; 2).
Задание 8
8.1. Даны вершины треугольника АВС. Составить а) уравнения сторон треугольника; б) уравнения высоты и медианы, проведённых из вершины В, если:
1) А(1; 2), В(5; 4), С(3; 6).
2) А(-1; 1), В(1; 4), С(3; 1).
3) А(2; 1), В(4; 5), С(6; 3).
4) А(3; -2), В(1; 1), С(-1; 6).
5) А(4; 1), В(3; -2), С(2; 5).
8.2. Даны прямые l1 и l2. Составить уравнения прямых, проходящих через их точку пересечения, а) параллельно прямой l3; б) перпендикулярно прямой l3; в) под углом 45 к l3, если:
1) l1: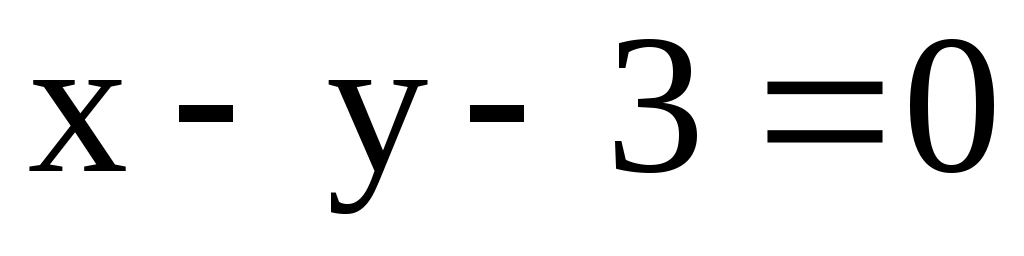 ; l2:
; l2: 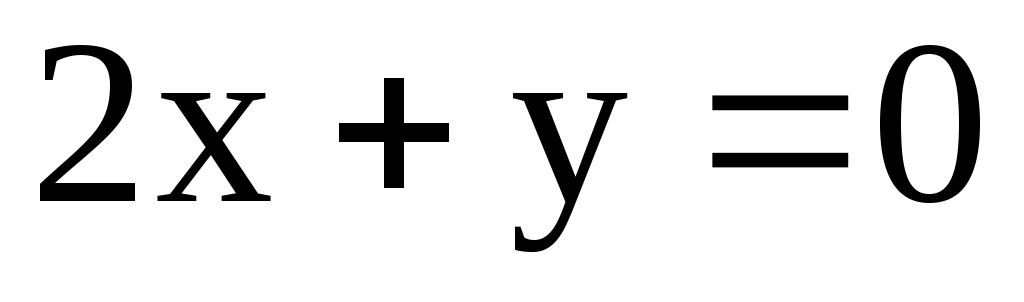 ; l3:
; l3: 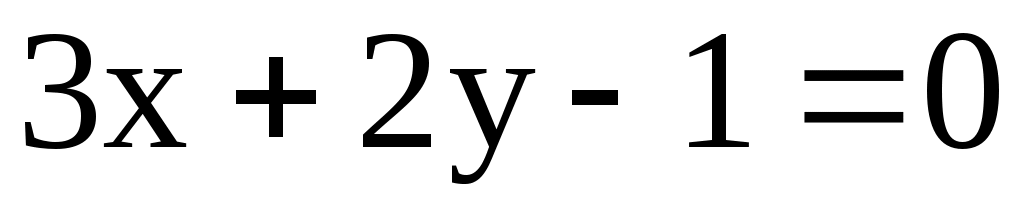 .
.
2) l1: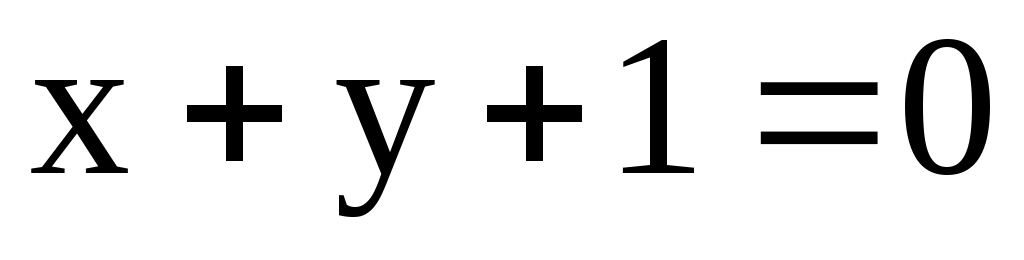 ; l2:
; l2: 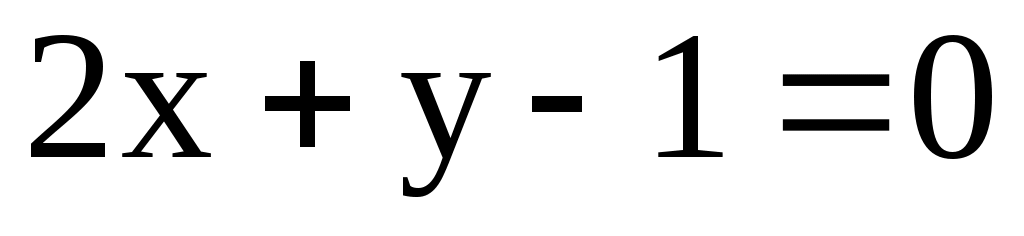 ; l3:
; l3: 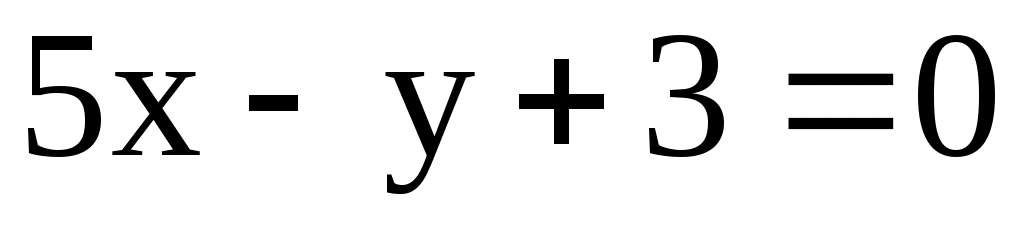 .
.
3) l1: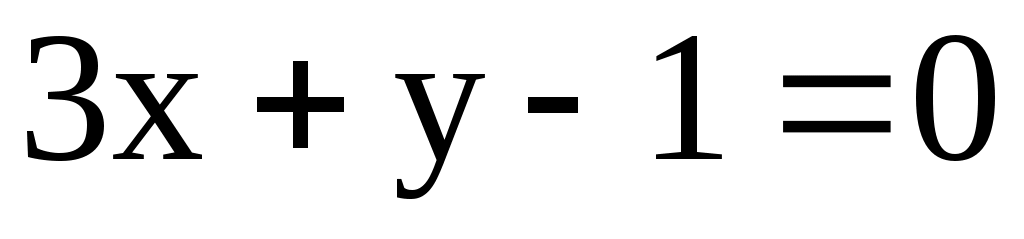 ; l2:
; l2:  ; l3:
; l3: 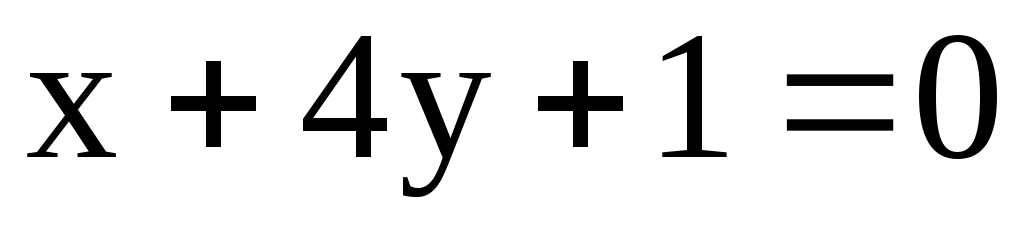 .
.
4) l1: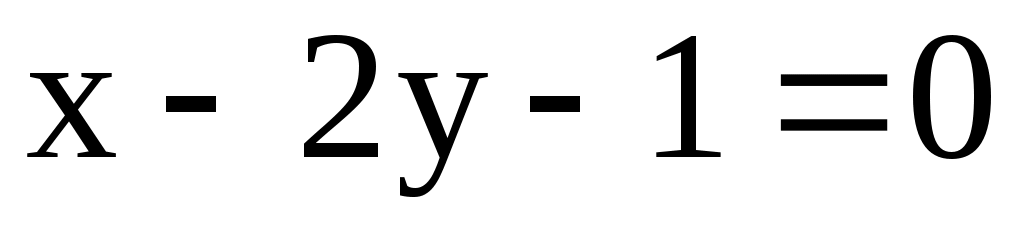 ; l2:
; l2: 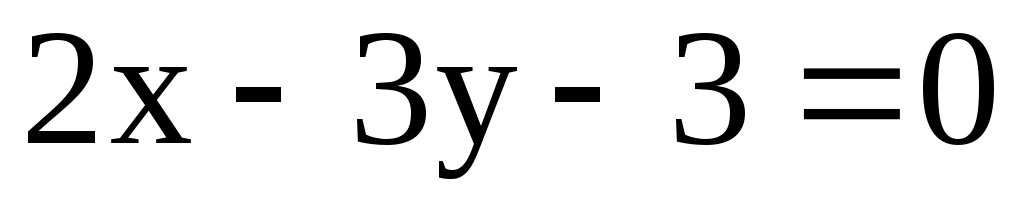 ; l3:
; l3: 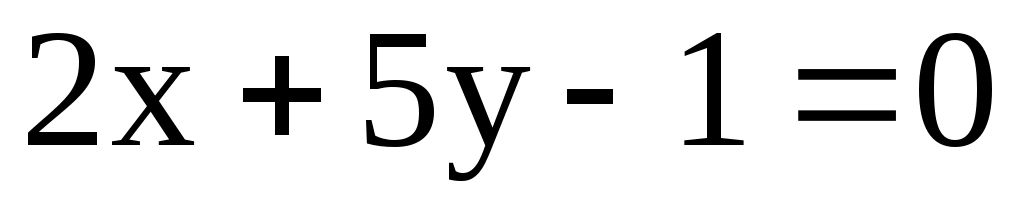 .
.
5) l1: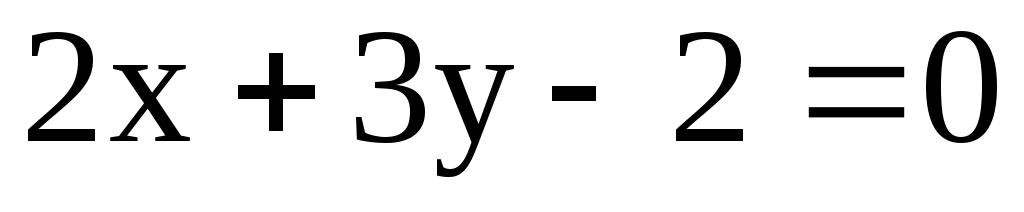 ; l2:
; l2: 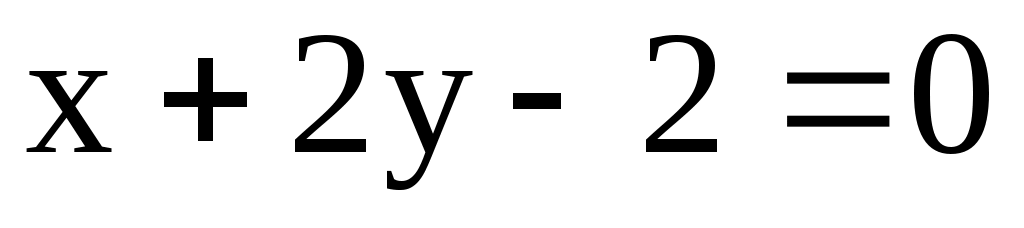 ; l3:
; l3: 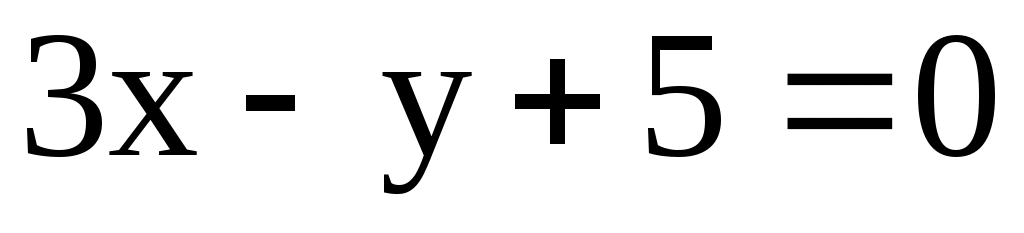 .
.
8.3. Даны координаты вершин треугольника АВС. Найти точки пересечения высот и медиан этого треугольника, если:
1) А(1; 0), В(3; 1), С(2; 2).
2) А(1; -1), В(4; 1), С(1; 3).
3) А(0; 1), В(4; 3), С(2; 5).
4) А(3; 3), В(5; 4), С(-1; -3).
5) А(-1; 2), В(3; 4), С(1; 0).
8.4. Найти проекцию точки М на прямую, проходящую через точки А и В, если:
1) М(1; -1), А(2; 2), В(0; 1).
2) М(-1; 3), А(1; 2), В(2; 1).
3) М(0; 2), А(1; -1), В(-1; 3).
4) М(2; 1), А(1; 5), В(-2; 2).
5) М(-3; 0), А(0; 1), В(1; 3).
8.5. Даны точки А, В и прямая l. Составить уравнения прямых, каждая из которых проходит через середину отрезка АВ и при этом: а) параллельна прямой l; б) перпендикулярна l; в) параллельна оси Oy; г) проходит через начало координат:
1) А(3; 1), В(-5; 3), l: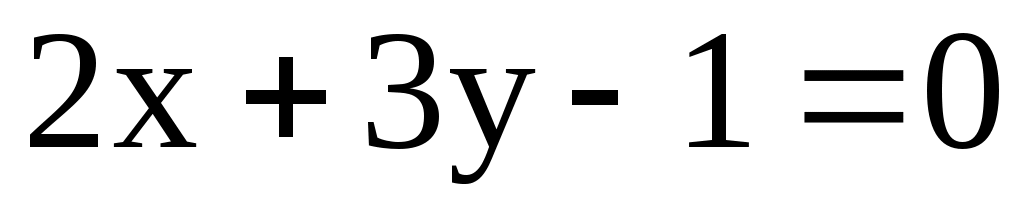 .
.
2) А(-1; 2), В(5; 6), l: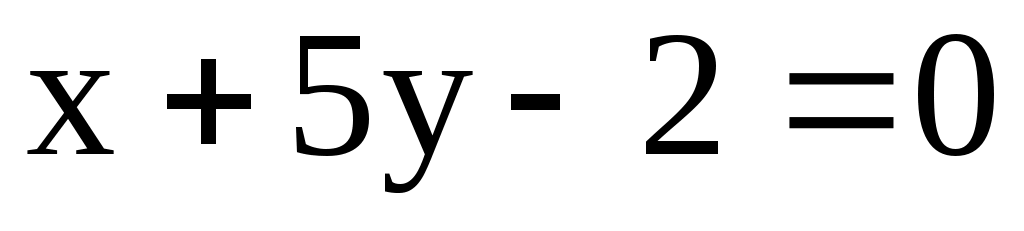 .
.
3) А(2; 2), В(4; -6), l: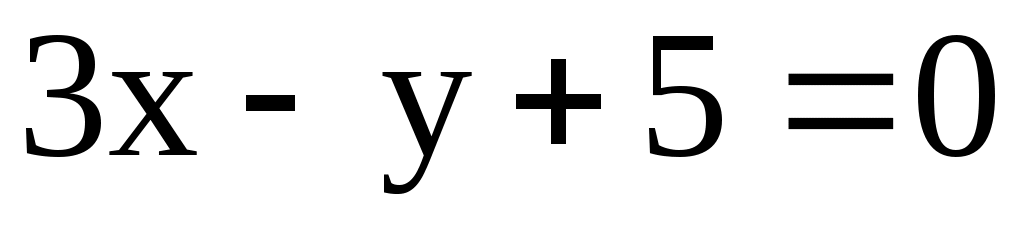 .
.
4) А(0; 4), В(4; -2), l: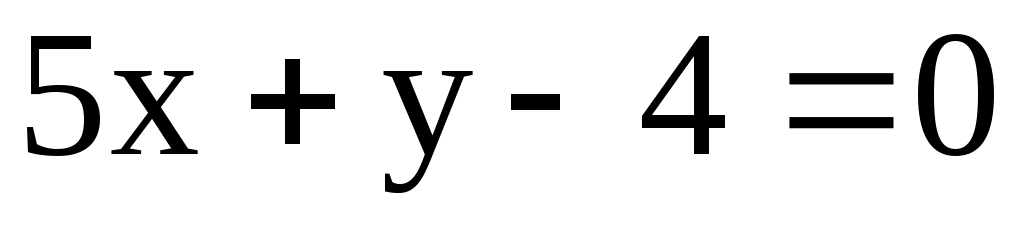 .
.
5) А(1; -1), В(5; 3), l: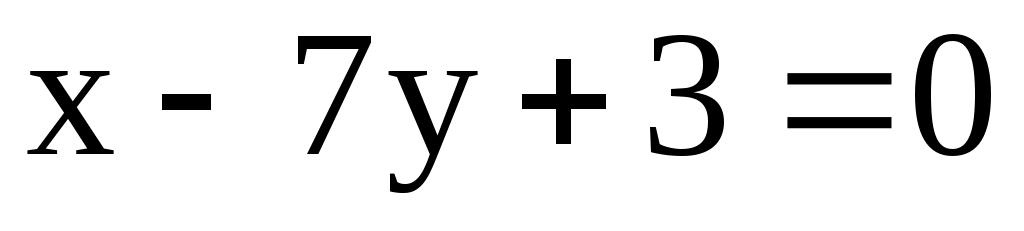 .
.
8.6. Найти координаты точки N, симметричной точке М относительно прямой, проходящей через точки А и В:
1) М(1; 3), А(2; 1), В(-4; -2).
2) М(-1; 2), А(2; -1), В(1; -2).
3) М(2; -1), А(1; 4), В(3; 2).
4) М(3; 0), А(2; -2), В(-4; 1).
5) М(0; -2), А(1; 3), В(3; 0).
Задание 9
9.1. Даны уравнения двух сторон прямоугольника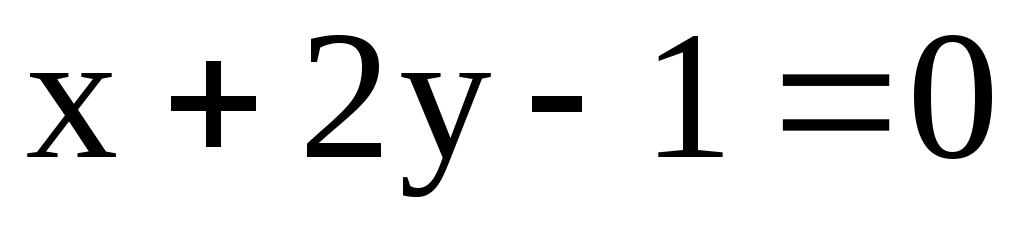 ,
, 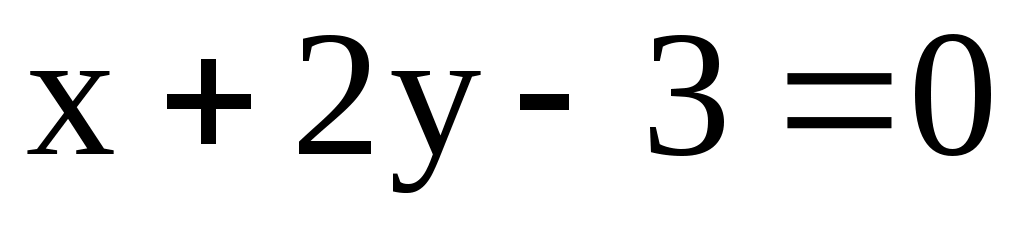 и одной из его диагоналей
и одной из его диагоналей 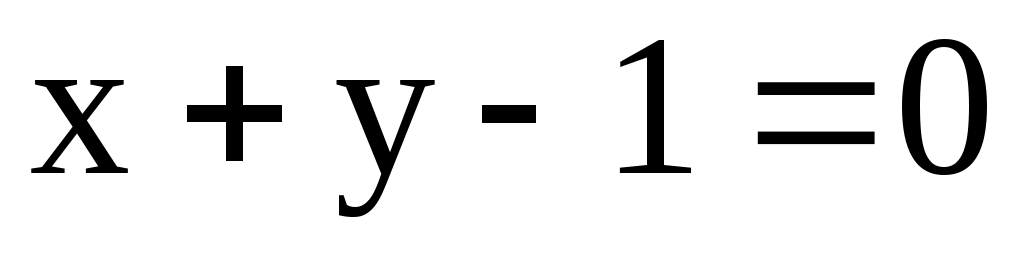 . Составить уравнения двух других сторон и второй диагонали.
. Составить уравнения двух других сторон и второй диагонали.
9.2. Даны уравнения двух сторон прямоугольника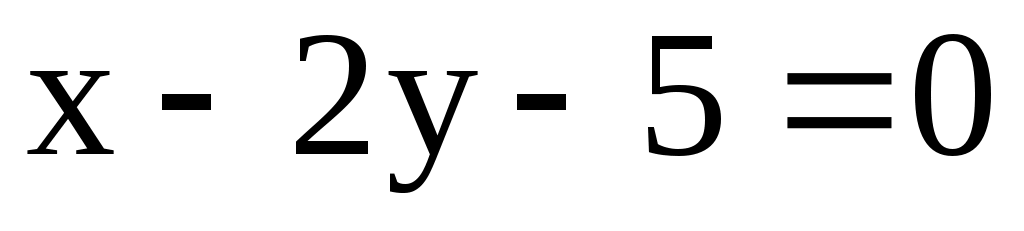 ,
, 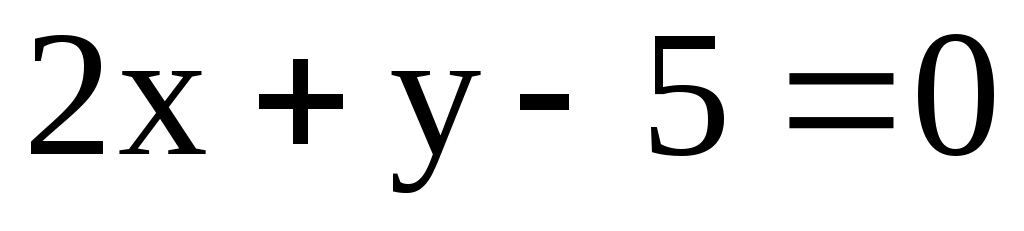 и уравнение одной из его диагоналей
и уравнение одной из его диагоналей 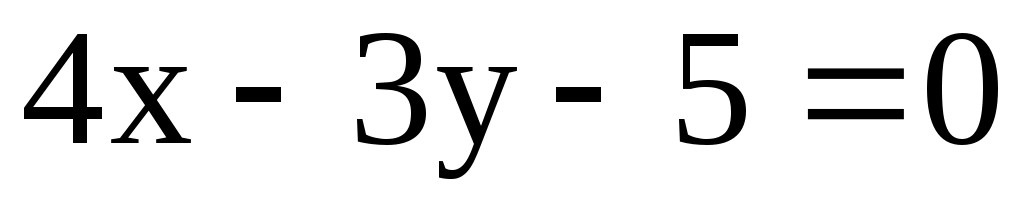 . Найти вершины прямоугольника.
. Найти вершины прямоугольника.
9.3. Даны уравнения двух сторон прямоугольника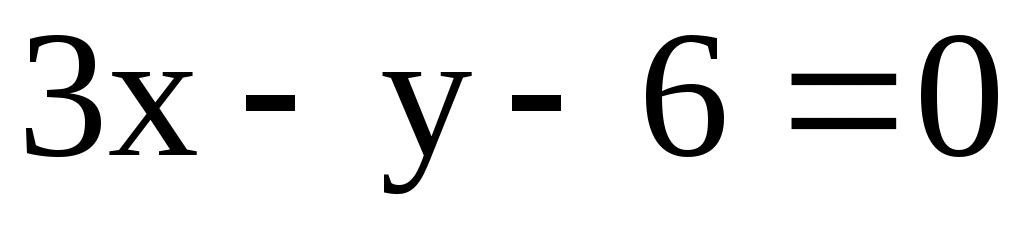 ,
, 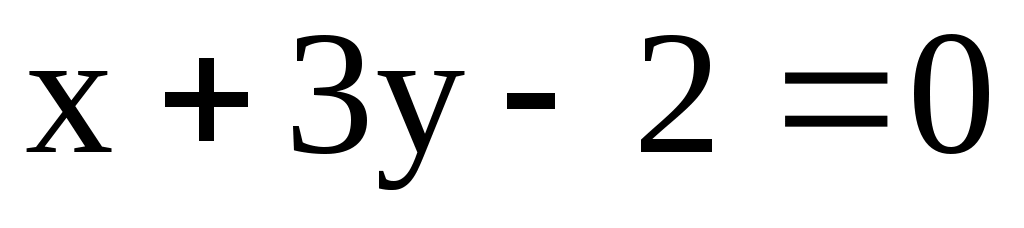 и одна из его вершин А(-1; 3). Составить уравнения двух других сторон этого прямоугольника.
и одна из его вершин А(-1; 3). Составить уравнения двух других сторон этого прямоугольника.
9.4. Даны уравнения двух сторон прямоугольника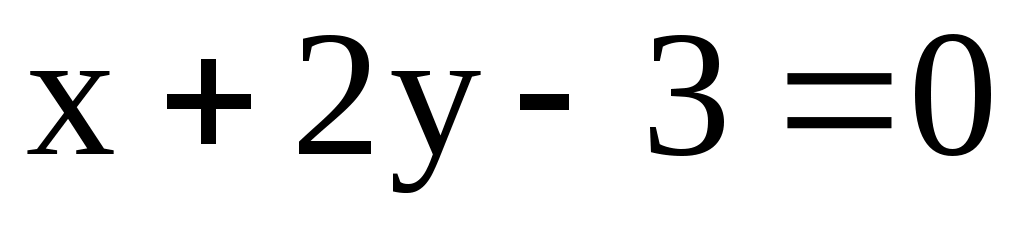 ,
, 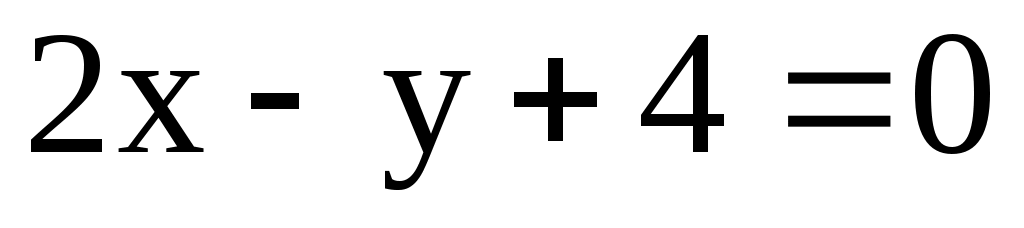 и одна из его вершин С(2; 3). Составить уравнения его диагоналей.
и одна из его вершин С(2; 3). Составить уравнения его диагоналей.
7.5. Даны точки A, B, C, D. При каком значении "t" тройка векторов
а) левой, если А(1; -2; 0), В(3; t; -2), С(0; 1; 5), D(2; 2; -1);
б) правой, если А(3; -1; 2), В(2; 2; 0), С(2t; 1; 3), D(0; -1; 3).
7.6. Проверить, лежат ли в одной плоскости точки A, B, C, и D:
а) А(-1; 2; 1), В(0; 1; -2), С(1; 3; -2) и D(2; 4; -3);
б) А(-1; 2; 1), В(-7; 0; -3), С(4; -1; 2) и D(-2; 1; 0).
7.7. При каком значении t точки A, B, C, и D лежат в одной плоскости, если:
а) А(2; 0; -1), В(1; 1; 0), С(0; -1; t) и D(-1; 2; 2);
б) А(-1; 3; 2), В(2t; -1; 1), С(t; 2; 0) и D(1; 1; 1).
7.8. При каком значении t компланарны векторы
а)
б)
7.9. Найти
7.10. Найти
,
7.11. При каком значении m векторы
7.12. Объём тетраэдра ABCD равен V. Найти координаты вершины D, если:
а) V = 2; А(2; 1; 3), В(3; 3; 2), С(1; 2; 4), DOz;
б) V = 3; А(1; 2; 3), В(3; 2; 1), С(2; 3; 1), DOx;
в) V = 5; А(2; 1; -1), В(3; 0; 1), С(2; -1; 3), DOy.
7.13. При каком значении m
7.14. При каком значении m
7.15. При каком значении m тройка векторов
7.16. При каком значении m
7.17. Векторы
(3; 3; -4) и
7.18. Найти единичный вектор, параллельный вектору
Задание 8
8.1. Даны вершины треугольника АВС. Составить а) уравнения сторон треугольника; б) уравнения высоты и медианы, проведённых из вершины В, если:
1) А(1; 2), В(5; 4), С(3; 6).
2) А(-1; 1), В(1; 4), С(3; 1).
3) А(2; 1), В(4; 5), С(6; 3).
4) А(3; -2), В(1; 1), С(-1; 6).
5) А(4; 1), В(3; -2), С(2; 5).
8.2. Даны прямые l1 и l2. Составить уравнения прямых, проходящих через их точку пересечения, а) параллельно прямой l3; б) перпендикулярно прямой l3; в) под углом 45 к l3, если:
1) l1:
2) l1:
3) l1:
4) l1:
5) l1:
8.3. Даны координаты вершин треугольника АВС. Найти точки пересечения высот и медиан этого треугольника, если:
1) А(1; 0), В(3; 1), С(2; 2).
2) А(1; -1), В(4; 1), С(1; 3).
3) А(0; 1), В(4; 3), С(2; 5).
4) А(3; 3), В(5; 4), С(-1; -3).
5) А(-1; 2), В(3; 4), С(1; 0).
8.4. Найти проекцию точки М на прямую, проходящую через точки А и В, если:
1) М(1; -1), А(2; 2), В(0; 1).
2) М(-1; 3), А(1; 2), В(2; 1).
3) М(0; 2), А(1; -1), В(-1; 3).
4) М(2; 1), А(1; 5), В(-2; 2).
5) М(-3; 0), А(0; 1), В(1; 3).
8.5. Даны точки А, В и прямая l. Составить уравнения прямых, каждая из которых проходит через середину отрезка АВ и при этом: а) параллельна прямой l; б) перпендикулярна l; в) параллельна оси Oy; г) проходит через начало координат:
1) А(3; 1), В(-5; 3), l:
2) А(-1; 2), В(5; 6), l:
3) А(2; 2), В(4; -6), l:
4) А(0; 4), В(4; -2), l:
5) А(1; -1), В(5; 3), l:
8.6. Найти координаты точки N, симметричной точке М относительно прямой, проходящей через точки А и В:
1) М(1; 3), А(2; 1), В(-4; -2).
2) М(-1; 2), А(2; -1), В(1; -2).
3) М(2; -1), А(1; 4), В(3; 2).
4) М(3; 0), А(2; -2), В(-4; 1).
5) М(0; -2), А(1; 3), В(3; 0).
Задание 9
9.1. Даны уравнения двух сторон прямоугольника
9.2. Даны уравнения двух сторон прямоугольника
9.3. Даны уравнения двух сторон прямоугольника
9.4. Даны уравнения двух сторон прямоугольника