Файл: Образовательная программа среднего профессионального образования Комплект контрольнооценочных средств по учебным.docx

Основные свойства алгоритмов следующие:

1.  Понятность для исполнителя — исполнитель алгоритма должен понимать, как его выполнять. Иными словами, имея алгоритм и произвольный вариант исходных данных, исполнитель должен знать, как надо действовать для выполнения этого алгоритма.

2.   Дискpетность (прерывность, раздельность) — алгоpитм должен пpедставлять пpоцесс pешения задачи как последовательное выполнение пpостых (или pанее опpеделенных) шагов (этапов).

3.   Опpеделенность — каждое пpавило алгоpитма должно быть четким, однозначным и не оставлять места для пpоизвола. Благодаpя этому свойству выполнение алгоpитма носит механический хаpактеp и не тpебует никаких дополнительных указаний или сведений о pешаемой задаче.

4.   Pезультативность (или конечность) состоит в том, что за конечное число шагов алгоpитм либо должен пpиводить к pешению задачи, либо после конечного числа шагов останавливаться из-за невозможности получить решение с выдачей соответствующего сообщения, либо неограниченно продолжаться в течение времени, отведенного для исполнения алгоритма, с выдачей промежуточных результатов.

Массовость означает, что алгоpитм pешения задачи pазpабатывается в общем виде, т.е. он должен быть пpименим для некотоpого класса задач, pазличающихся лишь исходными данными. Пpи этом исходные данные могут выбиpаться из некотоpой области, котоpая называется областью пpименимости алгоpитма.
На практике наиболее распространены следующие формы представления алгоритмов:
- словесная (запись на естественном языке);

- графическая (изображения из графических символов);

- псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы -естественного языка, общепринятые математические обозначения и др.);

- программная (тексты на языках программирования).
Основные алгоритмические конструкции: линейные, разветвляющиеся и циклические.

1.Базовая структура  "следование". Образуется последовательностью действий, следующих одно за другим.

2.Базовая структура  "ветвление". Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран. Структура ветвление существует в четырех основных вариантах:

---

если—то;

если—то—иначе;

выбор;

выбор—иначе.

3.Базовая структура  "цикл". Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.

3. 
   Логические основы алгоритмизации. Основы алгебры логики.
   

Алгеброй логики называется аппарат, который позволяет выполнять действия над высказываниями.

Алгебру логику называют также алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее  основные положения. В булевой  алгебре высказывания принято обозначать прописными латинскими буквами: A, B, X, Y. В алгебре Буля введены три основные логические операции с высказываниями? Сложение, умножение, отрицание. Определены аксиомы (законы) алгебры логики для выполнения этих операций. Действия, которые производятся над высказываниями, записываются в виде логических выражений.

4. 
   Логические операции: конъюнкция, дизъюнкция, инверсия, импликация, эквиваленция.
   

Операция И — логическое умножение (конъюнкция)

Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.

Операция ИЛИ — логическое сложение (дизъюнкция, объединение)

Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции ИЛИ является выражение, которое бу¬дет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений.

Операция НЕ — логическое отрицание (инверсия)

Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение.

Операция «ЕСЛИ-ТО» — логическое следование (импликация)

Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.

---

Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)

Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.

5. 
   Законы алгебры логики.
   

1. Закон одинарных элементов

2. Законы отрицания

a. Закон дополнительных элементов

 b. Двойное отрицание

  c. Закон отрицательной логики

3. Комбинационные законы

a. закон тавтологии (многократное повторение)

b. закон переместительности

c. закон сочетательности

d. закон распределительности

4. Правило поглощения (одна переменная поглощает другие)

5. Правило склеивания (выполняется только по одной переменной)

6. 
   Таблицы истинности.
   

Таблица истинности — это таблица, описывающая логическую функцию.

Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь».

Конъюнкция	Дизъюнкция	Сложение по модулю 2
Импликация		Эквиваленция
Штрих Шеффера	Стрелка Пирса	Отрицание

---

7. 
   Составление таблиц истинности для сложных логических функций.
   

Алгоритм построения таблиц истинности для сложных выражений:

1. 
   Определить количество строк:
   

количество строк = 2n + строка для заголовка,

n - количество простых высказываний.

2. 
   Определить количество столбцов:
   

количество столбцов = количество переменных + количество логических операций;

определить количество переменных (простых выражений);

определить количество логических операций и последовательность их выполнения.

3. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.

8. 
   Составление блок-схем алгоритмов.
   

Блок-схемой называют графическое представление алгоритма, в котором он изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.

В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.

Приведем наиболее часто употребляемые символы.

Название	Элемент	Комментарий
Процесс		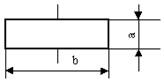Вычислительное действие или последовательность вычислительных действий
Решение		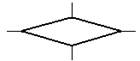Проверка условия
Модификация		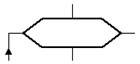Заголовок цикла
Предопределенный процесс		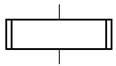Обращение к процедуре
Документ		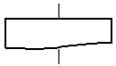Вывод данных, печать данных
Перфокарта		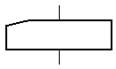Ввод данных
Ввод/Вывод		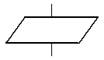Ввод/Вывод данных
Соединитель		Разрыв линии потока
Начало, Конец		Начало, конец, пуск, останов, вход и выход во вспомогательных алгоритмах
Комментарий		Используется для размещения надписей
Горизонтальные и вертикальные потоки		Линии связей между блоками, направление потоков
Слияние		Слияние линий потоков
Межстраничный соединитель		Нет

---

9. 
   Языки и системы программирования. Языки высокого и низкого уровня.
   

Язы́к программи́рования — формальная знаковая система, предназначенная для записи компьютерных программ. Язык программирования определяет набор лексических, синтаксических и семантических правил, задающих внешний вид программы и действия, которые выполнит исполнитель (компьютер) под её управлением.

Языки программирования низкого уровня.

Первые компьютеры приходилось программировать двоичными машинными кодами. Однако программировать таким образом - довольно трудоемкая и тяжелая задача. Для упрощения этой задачи начали появляться языки программирования низкого уровня, которые позволяли задавать машинные команды в понятном для человека виде. Для преобразования их в двоичный код были созданы специальные программы - трансляторы.

Языки программирования высокого уровня.

Особенности конкретных компьютерных архитектур в них не учитываются, поэтому созданные приложения легко переносятся с компьютера на компьютер. В большинстве случаев достаточно просто перекомпилировать программу под определенную компьютерную архитектурную и операционную систему. Разрабатывать программы на таких языках значительно проще и ошибок допускается меньше. Значительно сокращается время разработки программы, что особенно важно при работе над большими программными проектами.

10. 
    Правила записи выражений и операций. Типы данных. Синтаксис.
    

Типы данных Visual Basic.

Тип данных	Объем занимаемой памяти	Краткая запись
Целые типы
Integer (целое)	2 байта	%
Long (целое двойной длины)	4 байта	&
Byte (Байт)	1 байт
Boolean (булево)	2 байта
Плавающие типы
Single Десятичные числа	4 байта	!
Double Десятичные числа	8 байт	#
Строковые типы
String Текстовая информация	1 байт на каждый символ	$
Объектные типы
Object Рисунки или ссылки на любой другой объект	4 байта
Variant-типы
Variant (числовые типы)	16 байт
Variant (строковые типы)	22 байта +длина строки
Прочие типы
Currency Число в денежном формате	8 байт	@
Date Дата	8 байт

---