Файл: Решение задач оптимизации на максимизацию количества производимых товаров и услуг. Научный.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 46
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Научное общество учащихся.
Муниципальное бюджетное образовательное учреждение «Школа № 185» Ленинского района г. Н. Новгорода.
Решение задач оптимизации на максимизацию количества производимых товаров и услуг.
Научный руководитель:
Морозов Андрей Игоревич, Аспирант, старший преподаватель: НИУ ВШЭ в Нижнем Новгороде.
Выполнил: Киселёв Кирилл
ученик 11 «В» класса.
Консультант:
Бодякшина Наталья Александровна, учитель математики МБОУ «Школа №185»
Нижний Новгород
2022
Содержание
Введение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 3
1. Методологические основы решения оптимизационных задач…………4
1.1. Что такое «задачи на оптимизацию»? Что такое оптимизация? Каков математический смысл задач на оптимизацию? . . . . . . . . . . . . . . . . 6
1.2. Классификация типов задач и их методов решения………………6
2. Решение задачи с помощью логики……………………………………6
2.1 Производственная задача………………………………………………6
2.2. Внешнеторговая задача………………………………………………8
3. Решение задачи с помощью линейной функции………………………19
3.1. Задача про отель………………………………………………………20
3.2. Задача из ЕГЭ 11 класс……………………………………………….21
Заключение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 23
Введение
На уроке математики мы писали сочинение «Математика в жизни человека». Я задумался, где можно использовать математические знания в практической деятельности человека. Да, конечно, в магазине, надо считать деньги, взвешивать товар, рассчитывать стоимость покупки. А еще можно рассчитать время в пути, если знаешь расстояние и скорость. А интересно, можно рассчитать кротчайший путь между объектами, самую дешевую поездку.
Каждый человек время от времени оказывается в ситуации, когда достижение некоторого результата может быть осуществлено не единственным способом. В таких случаях приходится отыскивать наилучший способ. Однако в различных ситуациях наилучшими могут быть совершенно разные решения. Все зависит от выбранного или заданного критерия. На практике оказывается, что в большинстве случаев понятие «наилучший» может быть выражено количественными критериями – минимум затрат, минимум времени, максимум прибыли и т.д. Поэтому возможна постановка математических задач отыскания оптимального (optimum – наилучший) результата, так как принципиальных различий в отыскании наименьшего или наибольшего значения нет. Задачи на отыскание оптимального решения называются задачами оптимизации.
Научно-техническая революция, результаты которой особенно заметны в последние десятилетия, привела к созданию сложных высокопроизводительных систем и комплексов в различных сферах деятельности человека.
Ключевой проблемой решения этих сложных задач напрямую связано с решением задач оптимизации.
1. Методологические основы решения оптимизационных задач.
1.1. Что такое «задачи на оптимизацию»? Что такое оптимизация? Каков математический смысл задач на оптимизацию?
Задачи на оптимизацию – это блок экономических задач, для решения которых нужно найти наиболее выгодные условия для развития какого-либо предприятия.
Что такое оптимизация?
Из самого названия блока задач понятно, что нужно найти оптимальное решение. Когда у предпринимателя есть несколько путей развития своего бизнеса, ему нужно заранее просчитать, какой из них будет приносить больше прибыли. Он может выбрать один из них, а может их комбинировать. В таком случае встает вопрос о том, как это делать, с какого варианта начать и когда перейти ко второму.
Конкретных вопросов может быть огромное количество: с какого предприятия нанимать сотрудников, с какого завода закупать детали, как распределить зарплату и так далее. Этими вопросами занимается оптимизация.
Задачи оптимизации имеют огромное прикладное значение и возникают в самых разных разделах экономики, техники, военного дела. В таких задачах нас интересуют поиск некоторого оптимального решения (минимизующего или максимизирующего целевую функцию: прибыль, затраты, калорийность и т.п.) в условиях ограничений (наличия ресурсов, дорог, времени, продуктов и т.п.).
Каков математический смысл оптимизаций?
Конкретных формул для решения задач на оптимизацию нет. Нужно понимать, как связаны исходные данные с целью предпринимателя. Для этого составляются функции, описывающие зависимости прибыли от поставленных условий. При этом зачастую эти условия уже заданы функцией. В таком случае нужно понимать, что от чего зависит. Как прийти к такой функции, в которой присутствуют все условия, и при этом анализ данной функции показывает оптимальный вариант.
Если условие задано не функцией, а конкретными значениями, в любом случае, нужно будет найти зависимость между ними и искомой прибылью.
В задачах на оптимизацию нередко встречаются производные. Точки максимума и минимума могут
показать наибольшую и наименьшую прибыль, если функция составлена в зависимости от неё.
Задача №1.1:
Александр владеет двумя кондитерскими фабриками. На фабрике А делают 100 шоколадных тортов в день или 70 фруктовых. На заводе В делают 80 шоколадных или 90 фруктовых тортов в день. При этом известно, что на потребительском рынке шоколадный торт стоит 300 рублей, а фруктовый 400. Александру нужно выбрать, какой завод будет производить шоколадные торты, а какой фруктовые, с тем условием, что завод может производить только один тип тортов в день (то есть или шоколадные, или фруктовые), но затраты на их производство одинаковые. Какую максимальную прибыль в день может иметь Александр при имеющихся данных?
1.Фруктовые торты продаются по более высокой цене, при этом за день на фабрике В их делают больше. Очевидно, что этой фабрике стоит производить фруктовые торты. Тогда за день работы фабрики Александр будет получать максимальную прибыль с этого завода в размере:
S_{B} = 90∙400=36000
2.Независимо от завода фруктовые торты на рынке продаются дороже, но на фабрике А их делают медленнее. Нужно проверить, будет ли производство фруктовых тортов на этой фабрике более выгодным, чем производство шоколадных тортов несмотря на то, что их делают меньше. Сравним доход фабрики А от производства шоколадных и фруктовых тортов:
S_{AФ} = 70∙400=28000
S_{AШ} = 100∙300=30000
28000 <30000
3.Значит, фабрике А нужно производить шоколадные торты несмотря на то, что продаются по более низкой цене.
Найдем общий доход Александра за день, при условии, что фабрика А производит шоколадные торты, а фабрика В – фруктовые:
S_{B} + S_{A} = 36000+30000=66000
Ответ: 66000 (Конечно, в реальных ситуациях предприниматели учитывают гораздо больше факторов, таких, как себестоимость, объём спроса на конкретный вид товара, а также могут производить разные виды товара на одном заводе в определенных пропорциях.).
1.2. Классификация типов задач на оптимизацию.
Многие задачи оптимизации сводятся к отысканию наименьшего, (или наибольшего), значения целевой функции или показателя качества. В зависимости от вида целевой функции и вида ограничений на область и параметры функции различают несколько типов задач оптимизации.
Наиболее часто встречающиеся типы задач оптимизации – это
-
Производственная задача -
Внешнеторговая задача
Рассмотрим примеры некоторых типов задач оптимизации.
2. Решение задачи с помощью логики.
2.1. Производственная задача.
Общий вид задач:
Предприятие производит продукты
, 
, ..., 
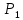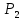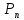. На производство одного продукта
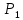потребуется затратить 
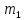материала и 
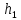человека - часов. Прибыль с первой проданной штуки - 
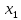и 
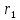кол – во товара для производства. На производство одного продукта
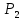потребуется затратить 
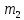материала и 
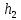человеко-часов. Прибыль с первой проданной штук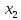и - 
и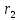 
кол – во товара для производства и т.д. На производство одного продукта
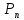потребуется затратить 
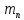материала и 
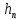человека - часов. Прибыль с первой проданной штук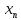и - 
и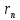 
кол – во товара для производства. Причём
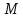– всего ресурса, а 
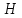– всего человеко-часов. Задача – произвести продукцию в таком объёме, чтобы прибыль оказалась максимальной.
Целевая функция:
+
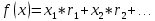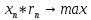– общая прибыль 
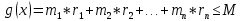– общая затрата материала
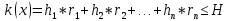- общая затрата человеко-часовЗадача №2.1.
Условие задачи:
Мебельная фабрика специализируется на производстве столов, стульев и табуреток. Затрата на производство одного стола потребуется
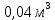древесины, а также 4 человека – часов, причем прибыль с этого составит 750 рублей. Затрата на производство одного стула потребуется 
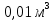древесины, а также 3,5 человека – часов, причем прибыль с этого составит 600 рублей. Затрата на производство одной табуретки потребуется 
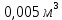и 1,5 человека – часов, причем прибыль с этого составит 250 рублей. Ресурсы ограничены и составляют 10 м3 древесины и 880 человеко-часов. Задача – произвести продукцию в таком объёме, чтобы прибыль оказалась максимальной.Пусть x – количество столов,
y – количество стульев,
z – количество табуреток.
Допущения в модели оптимизации:
- цены не зависят от объёма производства;
- норма затрат не зависит от объёмов производства.
| | Доход (руб.) | Расход древесины (м3) | Трудозатраты (чел/час) |
| Столы | 750 | 0,04 | 4 |
| Стулья | 600 | 0,01 | 3,5 |
| Табуретки | 250 | 0,005 | 1,5 |
Целевая функция:
750x+600y+250z → max
Решим систему:
750x+600y+250z → max
0,04x+0,01y+0,005z ≤ 10
4x+3,5y+1,5z ≤ 880
x, y, z ≥ 0
x, y, z – целые числа
Ответ: x=6, y=0, z=0