Файл: Решение задач оптимизации на максимизацию количества производимых товаров и услуг. Научный.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 48
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
≤ 120
Ограничения по объему экспорта:
x11+x21+x31 ≤ 42
x12+x22+x32 ≤ 80
x13+x23+x33 ≤ 70
Ограничения по объему импорта:
x14+x24+x34 ≤ 1800
x15+x25+x35 ≤ 250
Ограничения по рынкам:
x11+x12+x13 ≥ 750
x24+x25+x26 ≤ 1000
80x31+120x33– 5,8x34 – 8,1x35 =0
Решим систему уравнений:
130x11+160x21+80x31+390x12+250x22+170x13+190x23+120x33 – 7,3x14 – 10,5x24 –5,8x34 – 12,2 x15 – 8,1 x35 – 6,1x16 – 9,3x26 → max
x11 ≤ 30
x21 ≤ 27
x12 ≤ 22
x22 ≤ 8
x13 ≤ 35
x23 ≤ 30
x14 ≤ 820
x24 ≤ 600
x34 ≤ 930
x25 ≤ 370
x35 ≤ 120
x11+x21+x31 ≤ 42
x12+x22+x32 ≤ 80
x13+x23+x33 ≤ 70
x14+x24+x34 ≤ 1800
x15+x25+x35 ≤ 250
x11+x12+x13 ≥ 750
x24+x25+x26 ≤ 1000
80x31+120x33– 5,8x34 – 8,1x35 =0
Ответ:
x11=15, x21=27, x31=0, x12=22, x22=8, x32=0 (по условию задачи), x13=35, x23=30, x33=1,94452, x14=0, x24=0, x34=37,997, x15=0 (по условию задачи), x25=0, x35=1,6, x16=0, x26=0, x36=0 (по условию задачи)
Итак, чтобы максимизировать валютную выручку от экспорта необходимо, чтобы товары экспортировались и импортировались в следующих объёмах. Объём продажи товара А на рынке I должен составлять 15 тыс. единиц продукции; объём продажи товара А на рынке II - 27 тыс. единиц продукции; в то же время, на рынок III поставка товара А не должна осуществляться. Товар В на рынок I должен поставляться в количестве 22 тыс. единиц продукции; на рынок II товар В надо поставлять в количестве 8 тыс. единиц продукции; на рынок III товар В поставляться не будет по условию задачи. Объём продажи товара C на рынке I должен составлять 35 тыс. единиц продукции; объём продажи товара C на рынке II - 30 тыс. единиц продукции; объём продажи товара C на рынке III – 1,94452 тыс. единиц продукции. Товар D не должен импортироваться на I и II рынки, а на рынок III товар D должен импортироваться в объёме 37,997 тыс. Товар Е на рынок I не будет импортироваться по условию задачи
; на рынок II товар Е тоже не должен импортироваться; на рынок III товар Е надо импортировать в объёме 1,6 тыс. единиц продукции. Товар F на рынок III не импортируется по условию задачи. На рынки I и II товар F также импортировать не следует.
3. Решение задач с помощью линейной функции.
Перейдём к разбору задачи оптимизации с линейной целевой функцией, в которой связи между переменными даются только линейными уравнениями или линейными неравенствами.
Составляя математическую модель такой задачи, мы придём к традиционной с точки зрения элементарной математики задаче на метод областей. Это объясняется тем, что будет дана система линейных уравнений и неравенств, определяющих условия производства продукции или услуги, а также линейная функция с параметром, наибольшее или наименьшее значение которого надо найти. На координатной плоскости такая система задаёт многоугольник, расположенный в первой координатной четверти (поскольку в подобных задачах речь идёт о неотрицательных величинах). Графиком линейной функции является прямая, для которой можно найти требуемое значение параметра (например, максимальное значение, при котором указанная прямая будет иметь хотя бы одну общую точку с построенной областью). Эту прямую будем называть целевой прямой.
Общий вид задач:
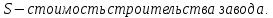
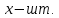
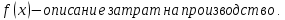
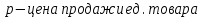
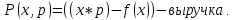
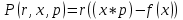
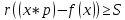
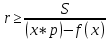
3.1. Задача про «отель».
Пример 3.1.
Условие задачи:
Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 21 квадратный метр и номера «люкс» площадью 49 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 1099 квадратных метров. Предприниматель может поделить эту площадь между номерами различных типов как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Пусть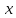
– это кол-во стандартных номеров, 
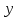– кол-во номеров «люкс». Они занимают площадь 
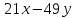. Составим равенство: 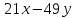= 1099. Выразим из этого равенства 
.
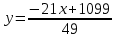Составим функцию заработанных денег:
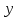. Далее подставим в эту функцию выражение для . Получим 
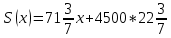. Это возрастающая линейная функция. Своё наибольшее значение оно принимает при наибольшем значении 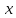и наименьшем значении 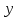. По условию 
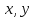– натуральные числа. Значит, 
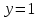(это наименьшее натуральное число) и 
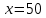. Значит, 
.
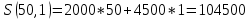Ответ: Предприниматель своего отеля за сутки может заработать 104500 рублей.
3.2. Задача из ЕГЭ 11 класс.
Пример 3.2.
Условие задачи:
Строительство нового завода стоит 78 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны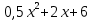
млн. рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит 
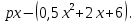Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более, чем за 3 года?
Решение.
Чтобы прибыль за три года была не меньше 78 млн руб. необходимо, чтобы ежегодная прибыль была не меньше 26 млн руб., то есть, чтобы выполнялось неравенство:
откуда, используя неравенство между средним арифметическим и средним геометрическим, получаем:
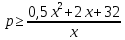
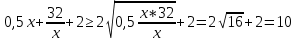
Удостоверимся, что это значение параметра достигается, то есть существует количество продукции x, при котором достигается эта цена.
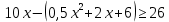
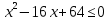
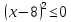
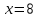
Тем самым, при p = 10 (цене 10 тыс. руб.) и x = 8 (производстве 8 тыс. единиц продукции), завод окупится за три года.
Ответ: p = 10.
Заключение
Большую часть своих усилий человек тратит на поиск наилучшего, т.е. оптимального решения поставленной задачи. Задачи подобного рода носят общее название – экономические задачи на оптимизацию или экстремальные задачи. Эти задачи тесно связаны с практической деятельностью человека. Как добиваться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени – так ставятся вопросы, над которыми приходится думать каждому члену общества. Экстремальные задачи с достаточной полнотой закладывают в сознание учащихся понимание того, как человек ищет, постоянно добивается решения жизненных задач, чтобы получающиеся результаты его деятельности были как можно лучшими.
Ограничения по объему экспорта:
x11+x21+x31 ≤ 42
x12+x22+x32 ≤ 80
x13+x23+x33 ≤ 70
Ограничения по объему импорта:
x14+x24+x34 ≤ 1800
x15+x25+x35 ≤ 250
Ограничения по рынкам:
x11+x12+x13 ≥ 750
x24+x25+x26 ≤ 1000
80x31+120x33– 5,8x34 – 8,1x35 =0
Решим систему уравнений:
130x11+160x21+80x31+390x12+250x22+170x13+190x23+120x33 – 7,3x14 – 10,5x24 –5,8x34 – 12,2 x15 – 8,1 x35 – 6,1x16 – 9,3x26 → max
x11 ≤ 30
x21 ≤ 27
x12 ≤ 22
x22 ≤ 8
x13 ≤ 35
x23 ≤ 30
x14 ≤ 820
x24 ≤ 600
x34 ≤ 930
x25 ≤ 370
x35 ≤ 120
x11+x21+x31 ≤ 42
x12+x22+x32 ≤ 80
x13+x23+x33 ≤ 70
x14+x24+x34 ≤ 1800
x15+x25+x35 ≤ 250
x11+x12+x13 ≥ 750
x24+x25+x26 ≤ 1000
80x31+120x33– 5,8x34 – 8,1x35 =0
Ответ:
x11=15, x21=27, x31=0, x12=22, x22=8, x32=0 (по условию задачи), x13=35, x23=30, x33=1,94452, x14=0, x24=0, x34=37,997, x15=0 (по условию задачи), x25=0, x35=1,6, x16=0, x26=0, x36=0 (по условию задачи)
Итак, чтобы максимизировать валютную выручку от экспорта необходимо, чтобы товары экспортировались и импортировались в следующих объёмах. Объём продажи товара А на рынке I должен составлять 15 тыс. единиц продукции; объём продажи товара А на рынке II - 27 тыс. единиц продукции; в то же время, на рынок III поставка товара А не должна осуществляться. Товар В на рынок I должен поставляться в количестве 22 тыс. единиц продукции; на рынок II товар В надо поставлять в количестве 8 тыс. единиц продукции; на рынок III товар В поставляться не будет по условию задачи. Объём продажи товара C на рынке I должен составлять 35 тыс. единиц продукции; объём продажи товара C на рынке II - 30 тыс. единиц продукции; объём продажи товара C на рынке III – 1,94452 тыс. единиц продукции. Товар D не должен импортироваться на I и II рынки, а на рынок III товар D должен импортироваться в объёме 37,997 тыс. Товар Е на рынок I не будет импортироваться по условию задачи
; на рынок II товар Е тоже не должен импортироваться; на рынок III товар Е надо импортировать в объёме 1,6 тыс. единиц продукции. Товар F на рынок III не импортируется по условию задачи. На рынки I и II товар F также импортировать не следует.
3. Решение задач с помощью линейной функции.
Перейдём к разбору задачи оптимизации с линейной целевой функцией, в которой связи между переменными даются только линейными уравнениями или линейными неравенствами.
Составляя математическую модель такой задачи, мы придём к традиционной с точки зрения элементарной математики задаче на метод областей. Это объясняется тем, что будет дана система линейных уравнений и неравенств, определяющих условия производства продукции или услуги, а также линейная функция с параметром, наибольшее или наименьшее значение которого надо найти. На координатной плоскости такая система задаёт многоугольник, расположенный в первой координатной четверти (поскольку в подобных задачах речь идёт о неотрицательных величинах). Графиком линейной функции является прямая, для которой можно найти требуемое значение параметра (например, максимальное значение, при котором указанная прямая будет иметь хотя бы одну общую точку с построенной областью). Эту прямую будем называть целевой прямой.
Общий вид задач:
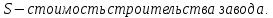
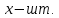
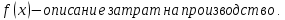
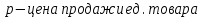
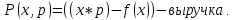
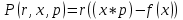
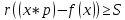
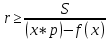
3.1. Задача про «отель».
Пример 3.1.
Условие задачи:
Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 21 квадратный метр и номера «люкс» площадью 49 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 1099 квадратных метров. Предприниматель может поделить эту площадь между номерами различных типов как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Пусть
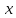– это кол-во стандартных номеров, 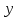– кол-во номеров «люкс». Они занимают площадь 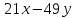. Составим равенство: 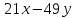= 1099. Выразим из этого равенства 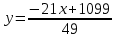.Составим функцию заработанных денег:
. Далее подставим в эту функцию выражение для 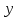. Получим 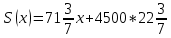. Это возрастающая линейная функция. Своё наибольшее значение оно принимает при наибольшем значении 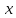и наименьшем значении 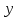. По условию 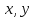– натуральные числа. Значит, 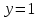(это наименьшее натуральное число) и 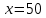. Значит, 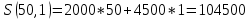.Ответ: Предприниматель своего отеля за сутки может заработать 104500 рублей.
3.2. Задача из ЕГЭ 11 класс.
Пример 3.2.
Условие задачи:
Строительство нового завода стоит 78 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны
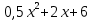млн. рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит 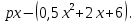Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более, чем за 3 года?Решение.
Чтобы прибыль за три года была не меньше 78 млн руб. необходимо, чтобы ежегодная прибыль была не меньше 26 млн руб., то есть, чтобы выполнялось неравенство:
откуда, используя неравенство между средним арифметическим и средним геометрическим, получаем:
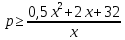
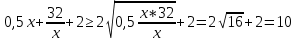
Удостоверимся, что это значение параметра достигается, то есть существует количество продукции x, при котором достигается эта цена.
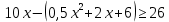
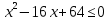
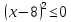
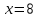
Тем самым, при p = 10 (цене 10 тыс. руб.) и x = 8 (производстве 8 тыс. единиц продукции), завод окупится за три года.
Ответ: p = 10.
Заключение
Большую часть своих усилий человек тратит на поиск наилучшего, т.е. оптимального решения поставленной задачи. Задачи подобного рода носят общее название – экономические задачи на оптимизацию или экстремальные задачи. Эти задачи тесно связаны с практической деятельностью человека. Как добиваться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени – так ставятся вопросы, над которыми приходится думать каждому члену общества. Экстремальные задачи с достаточной полнотой закладывают в сознание учащихся понимание того, как человек ищет, постоянно добивается решения жизненных задач, чтобы получающиеся результаты его деятельности были как можно лучшими.