Добавлен: 06.02.2019
Просмотров: 15992
Скачиваний: 9
206
Выраженная нелинейность вольтамперных характеристик керамики, наблюдаю-
щаяся даже в отсутствии выраженной асимметрии, свидетельствует о формировании на
межзеренных границах барьеров Шоттки. Транспорт заряда в этих условиях определя-
ется [593], как правило, либо надбарьерной термоэмиссией электронов (механизм
Шоттки), либо термическим возбуждением электрона проводимости с примесного
уровня, под действием электрического поля (механизм Френкеля-Пула). Для механизма
Шоттки ток в системе определяется выражением:
(
)
2
exp
exp
b
m
q
I
AT
E
kT
⎛
⎞
− φ
=
β
⎜
⎟
⎝
⎠
(64)
где
2
3
4
t
em k
A
h
π
=
— постоянная Ричардсона, q — заряд носителя тока,
b
φ — высота
потенциального барьера при нулевом напряжении,
0
4
e
e
kT
β =
πεε
i
,
m
U
E
d
=
— напря-
женность электрического поля, d — толщина барьера. То есть в этом случае I ~
exp(
E
m
½
). Нужно отметить, что в случае большей концентрации носителей в полупро-
воднике, когда не происходит полного обеднения в области барьера, выражение для
E
m
записывается значительно сложнее и в этих условиях
I ~ exp(E
m
¼
).
Для механизма Френкеля-Пула ток в системе определяется выражением:
(
)
0
exp
exp 2
t
m
m
E
I
E
E
kT
⎛
⎞
−
= σ
β
⎜
⎟
⎝
⎠
(65)
где
E
t
— энергия примесного уровня,
0
σ — проводимость материала при нулевом поле.
Таким образом, в этом случае зависимость тока в полупроводнике от приложенного
электрического поля: I/E
m
~ exp(
E
m
½
).
Кроме того, для неоднородных полупроводниковых систем, к которым относится
и исследуемая керамика, распределение примесей в материале носит статистический
характер, что приводит к значительным флуктуациям потенциала. В этом случае, неза-
висимо от способа преодоления барьера, становится применима перколяционная мо-
дель Шкловского [706], для которой зависимость тока в полупроводнике от приложен-
ного электрического поля:
0
exp
s
m
m
E
I
E
kT
⎛
⎞
β
⎜
⎟
= σ
⎜
⎟
⎝
⎠
(66)
где
0
0.25
s
eaV
β =
,
V
0
— амплитуда случайных колебаний потенциального рельефа,
a — характерный масштаб (период) колебаний, который для керамических материалов
207
может быть соотнесен с размером зерна керамики. Величина характерного масштаба
может быть оценена из диапазона омичности ВАХ (из напряженности поля, при кото-
рой появляются отклонения от линейной зависимости,
E
R
):
R
kT
a
eE
=
. Очевидно, что в
эксперименте в случае реализации данной модели, зависимость тока
I/E
m
~ exp(
E
m
½
)
идентична полученной в модели Френкеля-Пула. Различия между этими моделями за-
ключаются в физическом смысле коэффициентов, входящих в полное уравнение для
тока.
Анализ вольтамперных характеристик (как при наличии выраженной асимметрии,
так и при ее отсутствии), показал, что экспериментальные зависимости и при комнат-
ной и при повышенной температурах могут быть описаны моделями Френкеля-Пула
или Шкловского (рис. 162, 163). Следует отметить, что именно моделью Френкеля-
Пула описывается поведение большинства варисторных керамик на основе диоксида
олова [680–682]. Однозначный выбор между моделями Шкловского и Френкеля-Пула
невозможен, так как обе они приводят к корректным и самосогласованным величинам
параметров.
0
1
2
3
4
5
6
-8
-7
-6
-5
-4
-3
-2
-1
ln
I, [
A
/см
2
]
E
m
1/2
, B
1/2
/см
1/2
20
o
C
400
o
C
700
o
C
a
0
1
2
3
4
5
6
-6.0
-5.5
-5.0
-4.5
-4.0
-3.5
-3.0
ln
(I
/E
m
),
[A
/ В
см
]
E
m
1/2
, В
1/2
/см
1/2
20
o
C
400
o
C
700
o
C
б
Рис. 162. Вольтамперные характеристики внешнего слоя керамики (6.1 г/см
3
) после
100 часовых ресурсных испытаний в координатах уравнения Шоттки (а) и Френкеля-
Пула или Шкловского (б).
Таким образом, анализ объемной проводимости материала анодов подтвердил,
что при деградации керамики 97 мас.% SnO
2
+ 1.5 мас.% CuO + 1.5 мас.% Sb
2
O
3
при
электролизе в криолит-глиноземном расплаве в области межзеренных границ происхо-
дит формирование барьеров, препятствующих протеканию электрического тока. Ко-
нечно, при высоких температурах падение напряжения на них невелико, однако даже
незначительный перепад потенциала в несколько десятков милливольт может приво-
дить к существенному изменению скорости электрохимического процесса. С ростом
температуры можно предположить размывание барьеров на межзеренных границах из-
208
за увеличения фактора kT и роста числа носителей заряда в материале, что и приводит к
столь существенному различию в скоростях деградации керамики при различных тем-
пературах.
-20
-15
-10
-5
0
5
10
15
20
-0.20
-0.15
-0.10
-0.05
0.00
0.05
0.10
0.15
0.20
I, A/
см
2
E
m
, В/см
a
0
1
2
3
4
5
-8
-7
-6
-5
-4
-3
ln(
I/E
m
), [A
/
В
см
]
E
m
1/2
, В
1/2
/см
1/2
б
Рис. 163. Вольтамперные характеристики образцов керамики (6.1 г/см
3
) после 100 ча-
совых ресурсных испытаний в стандартных координатах (а) и в координатах уравне-
ния Френкеля-Пула или Шкловского (б). Измерение ВАХ — в режиме циклирования.
3.1.8. Туннельно-спектроскопическое исследование локальной проводимости
Метод сканирующей электронной микроскопии и локального микроанализа не
позволил обнаружить какую-либо неоднородность материала на микроуровне, которая
могла бы являться причиной столь неоднородной деградации керамики. Однако разра-
ботанная нами методика квазитопографического туннельно-спектроскопического кар-
тирования локальной проводимости позволила однозначно визуализировать области с
различными свойствами в объеме керамики. На рис. 164 представлены полученные од-
новременно: топографическое изображение поверхности, карты величины | d
I/dU | и
сдвига фаз между током и напряжением. Топографическое изображение не может дать
какой-либо информации о состоянии рабочей поверхности анода, так как образец перед
измерениями был отполирован. Наблюдаемый незначительный перепад высот на изо-
бражении не отвечает реальному топографическому рельефу, а связан с различием в
локальной проводимости материала, что подтверждается результатами квазитопогра-
фического картирования. Из рис. 164б хорошо видно, что на поверхности присутству-
ют замкнутые области с высокой проводимостью (d
I/dU велика, светлые области на
рис. 164б), разделенные прослойкой из значительно менее проводящего материала
(темные области). Толщина переходных областей составляет 200–500 нм. Более кон-
трастная фазовая карта (рис. 164в) является инвертированным отображением карты
| dI/dU | (увеличение dI/dU отвечает уменьшению вклада емкостной составляющей им-
педанса и, следовательно, уменьшению сдвига фаз между током и напряжением). Клас-
сические локальные вольтамперные спектры, измеренные в точках поверхности, отве-
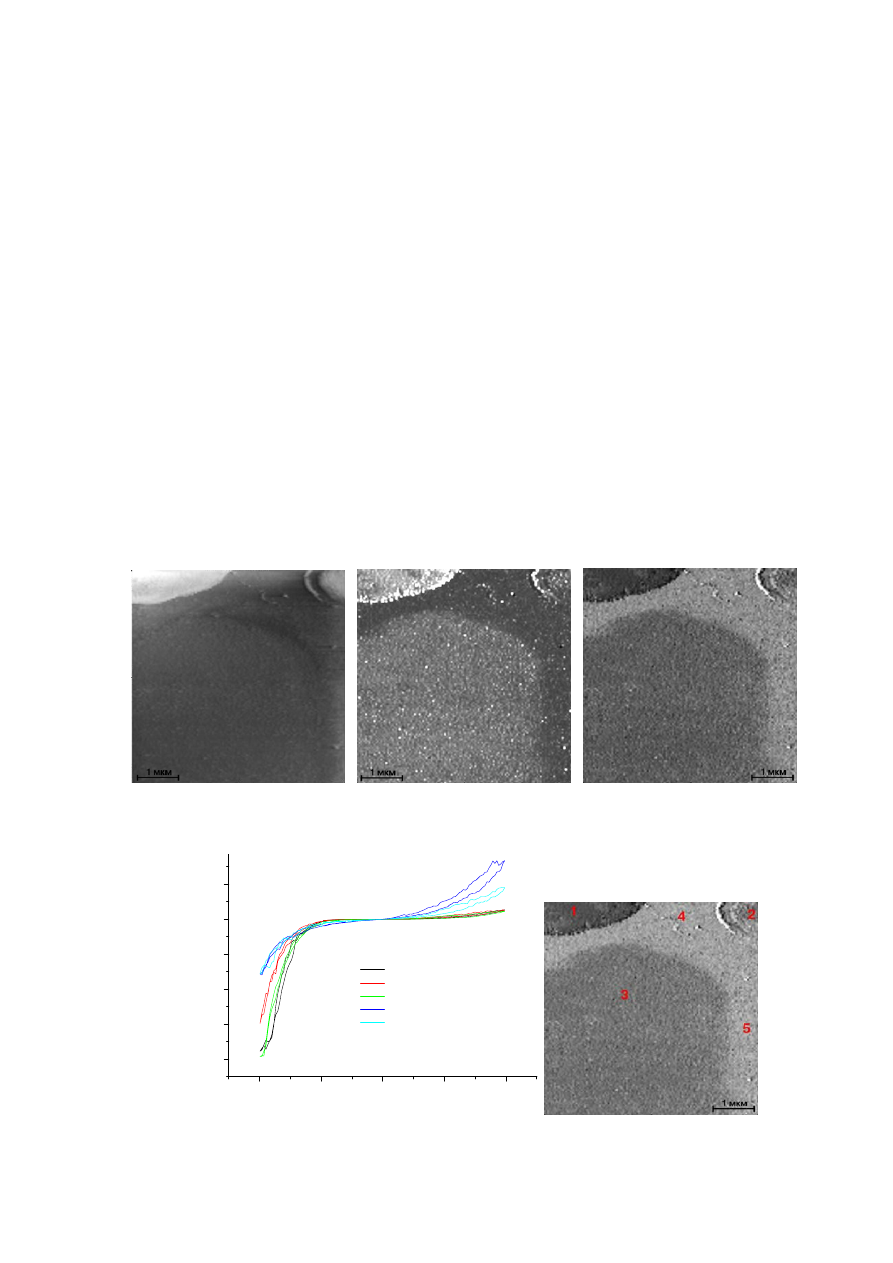
209
чающих зернам и межзеренным областям (рис. 165), подтверждают сделанные выводы.
В темных (рис 164в) хорошо проводящих областях регистрируются асимметричные
спектры, демонстрирующие высокую проводимость при отрицательных туннельных
напряжениях и очень низкую проводимость при положительных. Такое поведение ти-
пично для полупроводников n-типа (туннельный зазор представляет собой MIS диод,
возможно только туннелирование электронов с образца на иглу). В области межзерен-
ных границ регистрируются спектры, свидетельствующие о значительно более низкой
проводимости при отрицательных туннельных напряжениях и практически симметрич-
ные (кривые 4 и5 на рис. 165). Измерения вблизи поверхности образца (в области вы-
мывания спекающей добавки) (рис. 166) показывают, что в области пор (белые участки
на фазовой карте) различия в проводимости различных участков шлифа еще более уси-
ливаются (рис. 167). В некоторых точках регистрируются ВАХ
p-типа, то есть прово-
димость на этих участках выше при положительных туннельных напряжениях. К появ-
лению локальной проводимости
p-типа приводит также и окислительный отжиг шлифа
керамики на воздухе при 700
о
С (рис. 168).
a
б
в
Рис. 164. Результаты сканирования в дифференциальном режиме центральной части
образца керамики (6.1 г/см
3
) после 100-часовых ресурсных испытаний. a — топогра-
фия поверхности, б — величина |dI/dU|, в — сдвиг фаз между током и напряжением.
-1.0
-0.5
0.0
0.5
1.0
-20
-15
-10
-5
0
5
I
ту
н
, нА
U
тун
, В
1
2
3
4
5
Рис. 165. Локальные туннельные вольтамперные зависимости, измеренные в различ-
ных точках, отвечающих зернам и межзеренным областям на поверхности образца ке-
рамики (рис. 164).
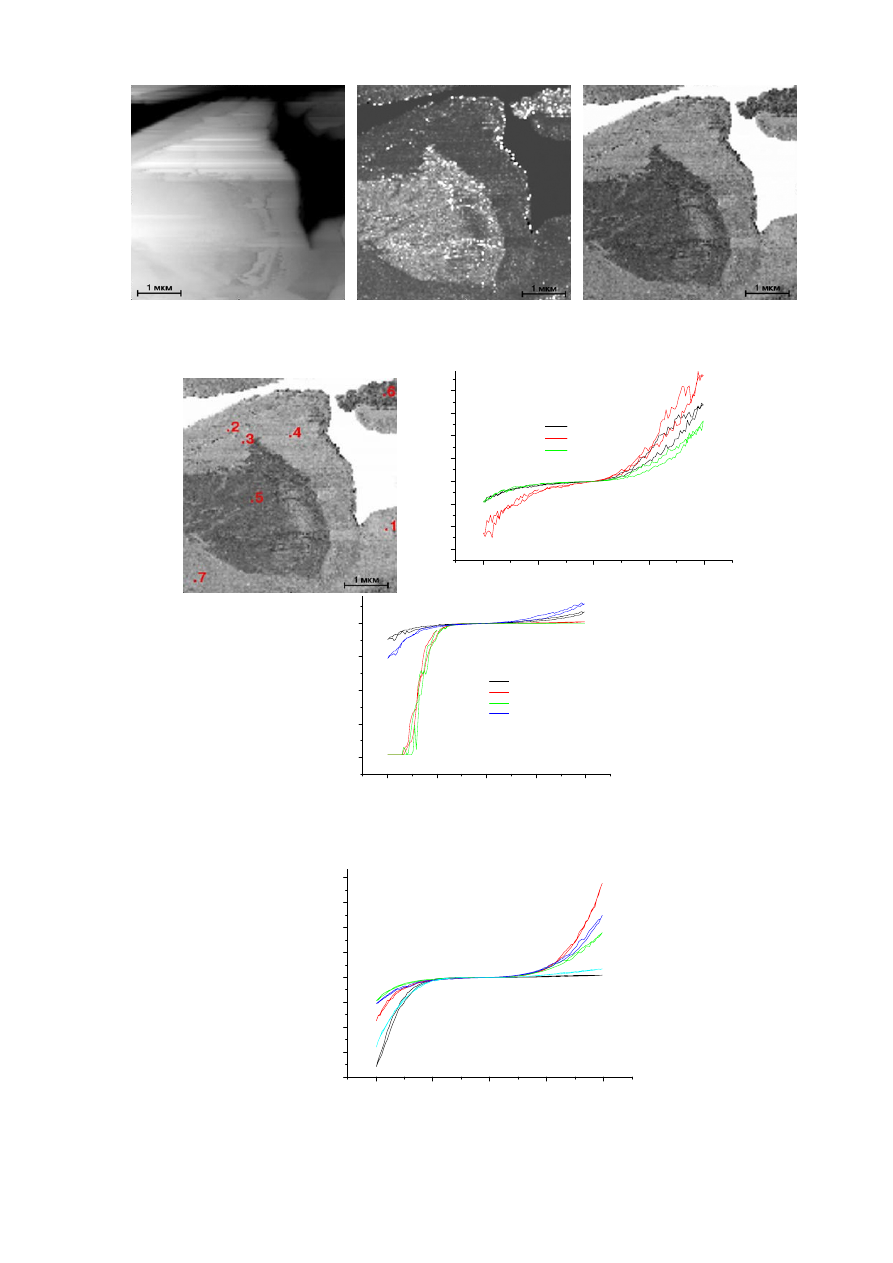
210
а
б
в
Рис. 166. Результаты сканирования в дифференциальном режиме продеградировавшего
участка керамики (6.1 г/см
3
) после 100-часовых ресурсных испытаний. a — топография
поверхности, б — величина |dI/dU|, в — сдвиг фаз между током и напряжением.
-1.0
-0.5
0.0
0.5
1.0
-6
-4
-2
0
2
4
6
8
I
ту
н
, нА
U
тун
, В
1
2
3
-1.0
-0.5
0.0
0.5
1.0
-20
-15
-10
-5
0
I
ту
н
, нА
U
тун
, В
4
5
6
7
Рис. 167. Локальные туннельные вольт-амперные зависимости, измеренные в различ-
ных точках, отвечающих зернам и межзеренным границам в области умеренной де-
градации образца керамики (6.1 г/см
3
) после 100-часовых ресурсных испытаний.
-1.0
-0.5
0.0
0.5
1.0
-20
-15
-10
-5
0
5
10
15
20
I
ту
н
, нА
U
тун
, В
Рис. 168. Локальные туннельные вольт-амперные зависимости, измеренные в различ-
ных точках, отвечающих зернам и межзеренным границам на поверхности образца
исходной керамики (6.1 г/см
3
) после термообработки при 700
о
С.