Шешуi : Есептiң шарты бойынша N=12 , m=5 , n=8. Кездейсоқ шама Х. Оның мүмкiн мәндерi : 1, 2, 3, 4, 5. Мұнда мүмкiн мәндер бiрден басталуының себебi : 5 бұйымның iшiнде кем дегенде бiр бұйым бiрiншi сортқа жатады.

Сонда


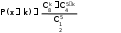
Ендi үлестiрiм кестесiн жазалық

Х	1	2	3	4	5
Р	0,0101	0,1414	0,4242	0,3535	0,0707

Е С Е П Т Е Р
84. Екi ойын сүйегiн (ойын кубын) бiр мезгiлде екi рет лақтырады. Осы тәжiрибеде Х-екi ойын сүйегiнде бiр мезгiлде жұп цифрдiң пайда болу санының биномдық үлестiрiм заңын жазу керек және M(x), D(x), (х) - тарды табу керек.

Нұсқау : Әрбiр ойын сүйегiнде жұп санның пайда болу ықтималдығы P₁ = P₂ =3/6 = 1/2. Ал екi ойын сүйегiнде бiр мезгiлде жұп цифр пайда болуының ықтималдығы

Р=P₁  P₂ = 0,25

85.Бiр ғана тәжiрибе жүргiзiледi. Нәтижесiнде А оқиғасы пайда болады, не пайда болмайды. А оқиғасының пайда болу ықтималдығы P. Кездейсоқ шама Х - А оқиғасының осы тәжiрибедегi пайда болу саны.

Осы кездейсоқ шаманың үлестiрiм заңын жазыңыз.

86. Екi атқыш нысанаға бiр-бiрден атыс жасады. Нысанаға тигiзу ықтималдығы бiрiншi атқыш үшiн 0,6 ал екiншiсiнiкi - 0,8. Кездейсоқ шама Х-нысанаға тигiзудiң саны. Осы кездейсоқ шаманың үлестiрiм кестесiн құрыңыз.

87. Тәуелсiз үш тәжiрибе жүргiзiлген, осылардың әрқайсысында А оқиғасы P = 0,4 ықтималдығымен пайда бола алады. Х - үш тәуелсiз тәжiрибелерде А оқиғасының пайда болу саны. Осы кездейсоқ шаманың үлестiрiм заңын жазыңыз.

88. Тиын елтаңба пайда болғанша лақтырылады. Лақтырыс санының үлестiрiм кестесiн жазыңыз.

Нұсқау: (2.1.3) формуланы пайдалану керек.

89. Тиын n рет лақтырылды. Х - пайда болған елтаңба саны. Осы кездейсоқ шаманың үлестiрiм кестесiн жазыңыз, М(х) , D(x) , (х) - табыңыз.

90. Екi ойын сүйегiн лақтырғанда пайда болатын сандардың қосындыларының үлестiрiм кестесiн жазыңыз.

91.Әрқайсысында А оқиғасы тұрақты Р ықтималдығымен пайда болатын тәуелсiз n тәжiрибе жүргiзiледi. Х - А оқиғасының пайда болу саны. Осы кездейсоқ шаманың үлестiрiм заңын жазыңыз,

M(x), D(x) табыңыз.

92. Урнада 2 ақ 3 қара шарлар бірдей бар. Урнадан ақ шар болғанша шар алынады, алынған шар түсiн анықтағансын қайтарылып отырады. Х - урнадан шар алудың саны. Осы кездейсоқ шаманың үлестiрiм кестесiн жазыңыз.

---

Нұсқау: (2.1.3) формуланы пайдалану керек.

93. Әрқайсысында тұрақты Р ықтималдығымен А оқиғасы пайда болатын n тәуелсiз тәжiрибелер жүргiзiледi. Х - А оқиғасының пайда болуының салыстырмалы жиiлiгi. Осы кездейсоқ шаманың үлестiрiм кестесiн құрыңыз.

94. Нысанаға тигiзу ықтималдығы 2/3 тең. Үш атыс жасағанда нысанаға тию санының үлестiрiм кестесiн құрыңыз.

95. Нысанаға тигiзу ықтималдығы Р. Тәуелсiз екi атыс жасалды. Х - нысанаға тиген оқ пен тимеген оқтың сандарының айырымы. Осы кездейсоқ шаманың үлестiрiм кестесiн құрыңыз.

96. Ойын кубы үш рет лақтырылған. Алты цифрының пайда болу санының үлестiрiм кестесiн жазыңыз.

97. Кездейсоқ шама Х а санына көбейтiлген. Сонда оның математикалық сипаттамалары қалай өзгередi?

98. Жарық беретiн торапқа 4 электр шамы қосылған. Әрбiр электр шамының бiр ай iшiнде жанып кету ықтималдығы 0,2. Х- бiр ай iшiнде жанып кеткен электр шамдарының саны.

Үлестiрiм кестесiн жазыңыз.

99. Кездейсоқ шама үлестiрiм қатарымен берiлген

Х	3 7 10 11
Р	0,4 0,1 0,2 0,3

М(Х), D(X), табыңыз.

100. Кездейсоқ шама үлестiрiм кестесiмен берiлген

Х	- 2	4	5	6
Р	0,3	0,1	0,2	0,4

М(Х), D(X), ₂(X), ₃(X) табыңыз.

101. Кездейсоқ шама үлестiрiм кестесiмен берiлген. Бастапқы ₁(X), ₂(X), ₃(X) және орталық ₃(X) моменттердi табыңыз.

Х	- 2	-1	0	1	2
Р	0,1	0,2	0,4	0,2	0,1

102.Екi тәуелсіз кездейсоқ шамалардың үлестiрiм заңдары берiлген.

Х	1	3				У	2	4
Р	0,4	0,6				Р	0,2	0,8

---

Z= Х+У кездейсоқ шаманың математикалық үмiтiн табыңыз.

103. 
     Екi тәуелсiз Х және У кездейсоқ шамаларының үлестiрiм заңдары берiлген
     

Х	1	4			У	0,5	2
Р	0,6	0,4			Р	0,8	0,2

Қосындының Z= Х+У дисперсиясын табыңыз.

104. Кездейсоқ шаманың үлестiрiм кестесi келтiрiлген

Х	1	2	3	4
Р	0,2	0,3	0,4	0,1

I, II, III және IV реттi орталық моменттердi табыңыз.

105. 
     .Тәуелсiз дискреттiк кездейсоқ шамалар Х және У үлестiрiм заңдарымен берiлген
     

Х	1	2			У	0,5	1
Р	0,2	0,8			Р	0,3	0,7

Математикалық үмiт М(ХУ)-ті табыңыз.

106.Тәуелсiз екi кездейсоқ шамалар Х және У үлестiрiм кестелерiмен берiлген

Х	4	6			У	1	2	4
Р	0,4	0,6			Р	0,3	0,4	0,3

Мына Z=XY кездейсоқ шаманың математикалық үмiтiн табыңыз.

107. Радиоаппаратура 1000 элементтен тұрады. Бiр жылдың iшiнде бiр элементтiң iстен шығу ықтималдығы 0,001 және ол басқа элементтерден тәуелсiз. 1. Тура екi элементтiң iстен шығу ықтималдығын табыңыз. 2. Кем дегенде екi элементтiң iстен шығу ықтималдығын табыңыз.

---

Нұсқау: n үлкен, p аз болғандықтан Пуассон заңын пайдалану керек.

108. Коммутаторға телефон соғу ықтималдығы бiр сағат iшiнде 0,01-ге тең. Телефон станциясына 300 абонент бекiтiлген. Бiр сағат iшiнде 4 абонент коммутаторға телефон соғудың ықтималдығы қандай?

109. Зауытта iстелген бұйымның бақылаудан өтпеуiнiң ықтималдығы 0,001. Бақылауға түскен 5000 бұйымның iшiнде бақылаудан өтпей қалған бұйымдардың саны бiреуден артық болмауының ықтималдығын табыңыз.

110. Фабрикадан келген бұйымдардың 1 пайызы жарамсыз болды. Алынған кез-келген 200 бұйымның iшiнде жарамсыз бұйымдар саны үшеуден артық болуының ықтималдығын табыңыз.

111. Қоймада барлығы 25 бұйым бар. Оның 5 бұйымы сапасыз. Қоймадан кез-келген 8 бұйым алынған. Алынған сегiз бұйымның iшiнде 3 сапасыз бұйым болатындығының ықтималдығы қандай?

---

§2. ҮЗIЛIССIЗ КЕЗДЕЙСОҚ ШАМАЛАР
Анықтама. Егер кездейсоқ шама өзiнiң мүмкiн мәндерiн [a,b] интервалында қабылдаса және бұл мәндердi нөмiрлеуге болмаса, онда ол үзiлiссiз кездейсоқ шама деп аталады.

Мысалы поездың кешiгу уақыты, атылған оқтың ұшу алыстығы т.б. үзіліссіз кездейсоқ шамалардың мысалдары болып табылады. Себебі бұл кездейсоқ шамалардың мүмкiн мәндерi белгiлi бiр интервалды қамтып жатады.

Кездейсоқ шаманың үлестiрiм заңдылықтарын әртүрлi жолмен қарастыруға болады. Төменде Х-кездейсоқ шаманың мүмкiн мәндерi тиянақты х санынан кiшi болу ықтималдығы қарастырылады.

Анықтама. Үлестiрiм функциясы деп Х-кездейсоқ шамасының мәндерi берілген х санынан кiшi болу ықтималдығын айтады.

Үлестiрiм функциясы F(x) арқылы белгiленедi. Сонда анықтама бойынша

F(x)=P(X
Бұл функцияны, сондай-ақ, интегралдық үлестiрiм функциясы деп те атайды.

Негiзгi қасиеттерi:
1.P(a  X  b)=F(b)-F(a)

2.F(x₂)  F(x₁), x₂ x₁ (2.2.1)

3.
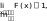
Дискреттiк кездейсоқ шама үшiн интегралдық үлестiрiм функция былай анықталады:

F(x)=P(X (2.2.2)
Мұндағы x₁, x₂ ... ,x_n дискреттiк кездейсоқ шаманың қабылдайтын мүмкiн мәндерi, ал p₁,p₂,...,р_n сол мәндердiң қабылдануының сәйкес ықтималдықтары. Мына (2.2.2) қоcындысы тек x_i < x теңсiздiгiн қанағаттандыратын барлық x_i үшiн олардың сәйкес ықтималдықтарының қосындысы болады; х берiлген тиянақты сан.

Анықтама: Үзiлiссiз кездейсоқ шаманың дифференциалдық функциясы (үлестiрiм тығыздығы) деп үлестiрiм функциясының бiрiншi туындысын айтады.

Дифференциалдық функцияны f(x) деп белгiлейдi. Сонда анықтама бойынша

f(x)=F ' (x) (2.2.3)

Негiзгi қасиеттерi:

1.

2.

3. 
   P(x)=
   

4. F(x)=

1-мысал. Айталық Х - дискреттiк кездейсоқ шама үлестiрiм кестесi арқылы берiлген болсын

---

Смотрите также файлы

• Программа среднего профессионального образования 40. 02. 01 Право и организация социального обеспечения Дисциплина Физическая культура (2 семестр) Практическое задание 7.doc

• Родной язык Вопросы к промежуточной аттестации.docx

• Все чаще в современном обществе на различных уровнях затрагивается проблема ухудшения состояния здоровья нации.docx

• Влияние вредных привычек на организм человека.odt

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx