Файл: Ытималдытар теориясы жне математикалы статистика i тарау. Кездейсо оиалар негізгі тсініктер. Оиаларды трлері.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 763
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
§1. ДИСКРЕТТIК КЕЗДЕЙСОҚ ШАМАЛАР
Анықтама. Кездейсоқ шаманың қабылдайтын мәндерiнiң саны ақырлы болса немесе тiзбек түрiнде жазылса, онда ондай кездейсоқ шамаларды дискреттiк кездейсоқ шамалар деп атайды.
Дискреттiк кездейсоқ шаманы анықтау үшiн үлестiрiм қатары - үлестiрiм кестесi құрылады
Бұл кестені үлестірім заңы деп те атайды.
Кестенiң жоғары жолында кездейсоқ шаманың мүмкiн мәндерi, ал төменгi жолында - сол мәндердiң сәйкес ықтималдықтары келтiрiлген.
Мұнда .
.
1.1. ҮЛЕСТIРIМ ЗАҢДАРЫ
1. БИНОМДЫҚ ҮЛЕСТIРIМ
Егер кездейсоқ шаманың мүмкiн мәндерi 0,1,2,..., к , ... болып, ал осы мүмкiн мәндердi Х=к қабылдау ықтималдықтары Бернулли формуласымен анықталса
 (2.1.1)
(2.1.1)
онда кездейсоқ шама Х биномдық үлестiрiм заңымен берiлген деп аталады.
Сонымен биномдық үлестiрiм заңдылығымен берiлген Х дискреттiк кездейсоқ шаманы - тұрақты ықтималдықты А оқиғасының n тәуелсiз сынақтарда пайда болуының саны ретiнде қарастыруға болады.
2. ПУАССОН ҮЛЕСТIРIМI
Егер тәуелсiз сынақтарда n үлкен сан болса және р-ның шамасы аз болса, онда Х-тәуелсіз сынақтарда А оқиғасының пайда болу саны кездейсоқ шамасының мүмкiн мәндерiнiң сәйкес ықтималдықтарын Пуассон формуласымен
P(X=к)=Pn(к) , =np (2.1.2)
, =np (2.1.2)
есептеу керек.
Бұл жағдайда кездейсоқ шама Пуассондық үлестiрiм заңымен берiлген дейдi. Бернулли схемасына негiзделген тағы да басқа үлестiрiмдердi келтiрелiк.
3. ГЕОМЕТРИЯЛЫҚ ҮЛЕСТIРIМ
Айталық тәуелсiз сынақтарда Бернулли схемасы қарастырылсын, мұнда P(A)=p. Сонда қатарынан (к-1) рет
 оқиғасы пайда болып, ал к -шы ретте А оқиғасының пайда болу ықтималдығы мына формуламен анықталады
оқиғасы пайда болып, ал к -шы ретте А оқиғасының пайда болу ықтималдығы мына формуламен анықталады
Г(к,р)=(1-р)к-1р (2.1.3)
Ықтималдығы осы формуламен анықталған мүмкін мәндері к=1,2,3...,n болатын кездейсоқ шаманы геометриялық үлестiрiмiмен берiлген дейдi.
4. ПАСКАЛЬ ҮЛЕСТIРIМI
Тәуелсiз сынақтарда оқиғасы қатарынан к-1 рет пайда болып, сосын А оқиғасы m рет пайда болуының ықтималдығы мына формуламен анықталады.
оқиғасы қатарынан к-1 рет пайда болып, сосын А оқиғасы m рет пайда болуының ықтималдығы мына формуламен анықталады.
 (2.1.4)
(2.1.4)
Мүмкін мәндері к=1,2,3...,n болатын , ықтималдығы (2.1.4)
формуламен анықталған кездейсоқ шама Паскаль үлестiрiмiмен берiлген дейдi. Геометриялық үлестiрiм Паскаль үлестiрiмiнiң жеке жағдайы, яғни m=1 болғанда геометриялық үлестiрiмдi аламыз.
5. ГИПЕРГЕОМЕТРИЯЛЫҚ ҮЛЕСТIРIМ
Егер X кездейсоқ шамасының мүмкiн мәндерi 0,1,2,3 ...к болып, ал сәйкес ықтималдықтары мына формуламен
 (2.1.5)
(2.1.5)
анықталса, онда кездейсоқ шама гипергеометриялық үлестiрiммен берiлген дейдi.
1- мысал. Жәшiкте барлығы 10 шар бар, олардың 7 - i қара 3-i көк шарлар. Жәшiктен кез-келген 5 шар алынды. Сол 5 шардың үшеуi қара болуының ықтималдығы қандай?
Шешуi: Осындай мазмұнды есептi классикалық анықтаманы және комбинаторикадағы қосу және көбейту ережелерiн пайдаланып шығаруға болады. Бұл есептi солай шығарса
 болады.
болады.
Ендi осы есептi жалпы түрде келтiрейiк.
2-мысал. Жәшiкте барлығы N шарлар бар, оның iшiнде n қара шар бар, ал (N-n) - көк шарлар. Жәшiктен кез-келген m шар алынды. Сол алынған m шардың iшiнде к қара шар болуының ықтималдығы қандай?
Шешуi: Х - жәшiктен алынған шарлар саны. Бұл кездейсоқ шаманың мүмкiн мәндерi 0, 1, 2, ..., m.
Жәшiктегi N шардан m шарды әртүрлi жолмен алуға болады, ал n қара шарлардан
жолмен алуға болады, ал n қара шарлардан
к шарды әртүрлi жолмен алуға болады, сонда алынған m шардың iшiнде m-к көк шарлар болғандықтан барлық N-n көк шарлардан m - к көк шарды
жолмен алуға болады, сонда алынған m шардың iшiнде m-к көк шарлар болғандықтан барлық N-n көк шарлардан m - к көк шарды  жолмен алуға болады. Сонымен жәшiктен алынған шардың к қара шарын
жолмен алуға болады. Сонымен жәшiктен алынған шардың к қара шарын  жолмен, ал қалған m-к көк шарды
жолмен, ал қалған m-к көк шарды  жолмен алуға болады екен. Олай болса комбинаторикадағы көбейту ережесiн қолдансақ, алынған m шардың iшiнде к - қара шар, m-к - көк шар болуы
жолмен алуға болады екен. Олай болса комбинаторикадағы көбейту ережесiн қолдансақ, алынған m шардың iшiнде к - қара шар, m-к - көк шар болуы 
 жолмен анықталады.
жолмен анықталады.
Сонда ықтималдықтың классикалық анықтамасы бойынша
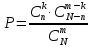
болады. Енді осы формуланы алдындағы есепке қолдансақ р=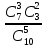 аламыз.
аламыз.
Сөйтiп X-кездейсоқ шама гипергеометриялық үлестiрiммен берiлгенiне көз жеткiздiк
.
1.2. ДИСКРЕТТIК КЕЗДЕЙСОҚ ШАМАЛАРДЫҢ САНДЫҚ
СИПАТТАМАЛАРЫ
Кездейсоқ шама өзінің үлестірім заңымен толық анықталады. Алайда көп жағдайда кездейсоқ шаманың үлестірім заңын анықтауға мүмкіндік болмайды. Осындай жағдайларда кездейсоқ шамаларды білгілі бір дәрежеде сипаттайтын сипаттамалардың қажеттігі туындайды. Мұндай сипаттамаларға сандық сипаттамалар деп аталатын сипаттамалар жатады. Олардың ішінде маңызды орын алатын сипаттамаға математикалық үміт деп аталатын сипаттаманы жатқызуға болады.
Дискреттiк кездейсоқ шаманың математикалық үмiті деп оның мүмкiн мәндерiнiң сәйкес ықтималдықтарына көбейтiндiлерiнiң қосындысын айтады:
 (2.1.6)
(2.1.6)
Математикалық үміт кездейсоқ шаманың мүмкін мәндерінің арифметикалық орташа мәніне жуықтап тең болады. Бұл математикалық үміттің ықтималдықтық мағынасы болып табылады.
Дискреттiк кездейсоқ шаманың
дисперсиясы деп, оның өзiнiң математикалық үмiтiнен ауытқуының квадратының математикалық үмiтiн айтады:
 (2.1.7)
(2.1.7)
Дисперсия кездейсоқ шаманың мүмкін мәндерінің өзінің математикалық үмітінен қаншалықты алшақ жатқандығын сипаттайтын шама болып табылады.
Дисперсияны есептеудiң жеңiлдетiлген формуласы :
 (2.1.8)
(2.1.8)
Дискреттiк кездейсоқ шаманың орташа квадраттық ауытқуы мына формуламен есептелiнедi:

Дискреттiк кездейсоқ шаманың к - реттi бастапқы моментi деп осы кездейсоқ шаманың к-шы дәрежесiнiң математикалық үмiтiн айтады:
 (2.1.9)
(2.1.9)
Дискреттiк кездейсоқ шаманың к - реттi орталық моментi деп, оның өзiнiң математикалық үмiтiнен ауытқуының к-шы дәрежесiнiң математикалық үмiтiн айтады :
 (2.1.10)
(2.1.10)
Кездейсоқ шаманың математикалық үмiтi бiрiншi бастапқы моментiне, ал дисперсиясы - екiншi орталық моментiне тең :
 ,
, 
Сондай-ақ екiншi, үшiншi және төртiншi ретті орталық моменттер
бастапқы моменттер арқылы төмендегiдей өрнектеледi :
 ,
,  ,
,
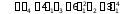 (2.1.11)
(2.1.11)
Дискреттiк кездейсоқ шаманың ең ықтималды мәнiн оның Модасы (M0) деп атайды.
Айталық кездейсоқ шаманың n мүмкiн мәндерi болсын. Егер

теңдiгi орындалса, онда кездейсоқ шаманың медианасы деп аталады.
кездейсоқ шаманың медианасы деп аталады.
Егер n=2к болса, онда
, егерде n=2к+1 болса, онда ;
;
Сондай-ақ қарастырылып отырған кездейсоқ шаманың үлестiрiм заңын қалыпты үлестiрiммен салыстыру үшiн Еk эксцесс және Аs асимметрия сипаттамалары қарастырылады. Мұнда
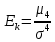 -3,
-3, 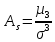
Ескерту : қалыпты үлестiрiм үшiн Ek = 0 , As = 0
Математикалық үмiттiң қасиеттерi
1. М(с) = с , 2. М(сх) = сМ(х)
3. М(х у) = М(х) М(у) 4. M(xy) = M(x)M(y)( мұнда Хжәне У тәуелсіз шамалар)
Дисперсияның қасиеттерi
1. D(x) 0 , 2. D(c) = 0
3. D(cx) = c2 D(x) 4. D(x y) = D(x) + D(y)
Мұндағы x және y тәуелсiз кездейсоқ шамалар.
Жоғарыда келтiрiлген үлестiрiм заңдарының математикалық үмiттерi мен дисперсияларын келтiрелiк.
1. Биномдық үлестiрiм
M(x) = np, D(x) = npq, ,
, 
M(x) = , D(x) = , ,
, 
3. Геометриялық үлестiрiм
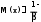 ,
,  (2.1.12)
(2.1.12)
4. Паскаль үлестiрiмi
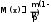 ,
, 
5. Гипергеометриялық үлестiрiм

Мұнда m < 0,1N болғанда D(x) npq болады, яғни биномдық үлестiрiмнiң дисперсиясына жуықтап тең болады.
Сондықтан m < 0,1N болғанда

болады. Осы жағдайда болады.
болады.
3-мысал. Дискреттiк кездейсоқ шама мына үлестiрiммен берiлсiн
Анықтама. Кездейсоқ шаманың қабылдайтын мәндерiнiң саны ақырлы болса немесе тiзбек түрiнде жазылса, онда ондай кездейсоқ шамаларды дискреттiк кездейсоқ шамалар деп атайды.
Дискреттiк кездейсоқ шаманы анықтау үшiн үлестiрiм қатары - үлестiрiм кестесi құрылады
| Х | x1 | x2 | x3 | ... | xn |
| p | p1 | p2 | p3 | ... | pn |
Бұл кестені үлестірім заңы деп те атайды.
Кестенiң жоғары жолында кездейсоқ шаманың мүмкiн мәндерi, ал төменгi жолында - сол мәндердiң сәйкес ықтималдықтары келтiрiлген.
Мұнда
1.1. ҮЛЕСТIРIМ ЗАҢДАРЫ
1. БИНОМДЫҚ ҮЛЕСТIРIМ
Егер кездейсоқ шаманың мүмкiн мәндерi 0,1,2,..., к , ... болып, ал осы мүмкiн мәндердi Х=к қабылдау ықтималдықтары Бернулли формуласымен анықталса
онда кездейсоқ шама Х биномдық үлестiрiм заңымен берiлген деп аталады.
Сонымен биномдық үлестiрiм заңдылығымен берiлген Х дискреттiк кездейсоқ шаманы - тұрақты ықтималдықты А оқиғасының n тәуелсiз сынақтарда пайда болуының саны ретiнде қарастыруға болады.
2. ПУАССОН ҮЛЕСТIРIМI
Егер тәуелсiз сынақтарда n үлкен сан болса және р-ның шамасы аз болса, онда Х-тәуелсіз сынақтарда А оқиғасының пайда болу саны кездейсоқ шамасының мүмкiн мәндерiнiң сәйкес ықтималдықтарын Пуассон формуласымен
P(X=к)=Pn(к)
есептеу керек.
Бұл жағдайда кездейсоқ шама Пуассондық үлестiрiм заңымен берiлген дейдi. Бернулли схемасына негiзделген тағы да басқа үлестiрiмдердi келтiрелiк.
3. ГЕОМЕТРИЯЛЫҚ ҮЛЕСТIРIМ
Айталық тәуелсiз сынақтарда Бернулли схемасы қарастырылсын, мұнда P(A)=p. Сонда қатарынан (к-1) рет
Г(к,р)=(1-р)к-1р (2.1.3)
Ықтималдығы осы формуламен анықталған мүмкін мәндері к=1,2,3...,n болатын кездейсоқ шаманы геометриялық үлестiрiмiмен берiлген дейдi.
4. ПАСКАЛЬ ҮЛЕСТIРIМI
Тәуелсiз сынақтарда
Мүмкін мәндері к=1,2,3...,n болатын , ықтималдығы (2.1.4)
формуламен анықталған кездейсоқ шама Паскаль үлестiрiмiмен берiлген дейдi. Геометриялық үлестiрiм Паскаль үлестiрiмiнiң жеке жағдайы, яғни m=1 болғанда геометриялық үлестiрiмдi аламыз.
5. ГИПЕРГЕОМЕТРИЯЛЫҚ ҮЛЕСТIРIМ
Егер X кездейсоқ шамасының мүмкiн мәндерi 0,1,2,3 ...к болып, ал сәйкес ықтималдықтары мына формуламен
анықталса, онда кездейсоқ шама гипергеометриялық үлестiрiммен берiлген дейдi.
1- мысал. Жәшiкте барлығы 10 шар бар, олардың 7 - i қара 3-i көк шарлар. Жәшiктен кез-келген 5 шар алынды. Сол 5 шардың үшеуi қара болуының ықтималдығы қандай?
Шешуi: Осындай мазмұнды есептi классикалық анықтаманы және комбинаторикадағы қосу және көбейту ережелерiн пайдаланып шығаруға болады. Бұл есептi солай шығарса
Ендi осы есептi жалпы түрде келтiрейiк.
2-мысал. Жәшiкте барлығы N шарлар бар, оның iшiнде n қара шар бар, ал (N-n) - көк шарлар. Жәшiктен кез-келген m шар алынды. Сол алынған m шардың iшiнде к қара шар болуының ықтималдығы қандай?
Шешуi: Х - жәшiктен алынған шарлар саны. Бұл кездейсоқ шаманың мүмкiн мәндерi 0, 1, 2, ..., m.
Жәшiктегi N шардан m шарды әртүрлi
к шарды әртүрлi
Сонда ықтималдықтың классикалық анықтамасы бойынша
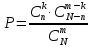
болады. Енді осы формуланы алдындағы есепке қолдансақ р=
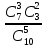 аламыз.
аламыз.Сөйтiп X-кездейсоқ шама гипергеометриялық үлестiрiммен берiлгенiне көз жеткiздiк
.
1.2. ДИСКРЕТТIК КЕЗДЕЙСОҚ ШАМАЛАРДЫҢ САНДЫҚ
СИПАТТАМАЛАРЫ
Кездейсоқ шама өзінің үлестірім заңымен толық анықталады. Алайда көп жағдайда кездейсоқ шаманың үлестірім заңын анықтауға мүмкіндік болмайды. Осындай жағдайларда кездейсоқ шамаларды білгілі бір дәрежеде сипаттайтын сипаттамалардың қажеттігі туындайды. Мұндай сипаттамаларға сандық сипаттамалар деп аталатын сипаттамалар жатады. Олардың ішінде маңызды орын алатын сипаттамаға математикалық үміт деп аталатын сипаттаманы жатқызуға болады.
Дискреттiк кездейсоқ шаманың математикалық үмiті деп оның мүмкiн мәндерiнiң сәйкес ықтималдықтарына көбейтiндiлерiнiң қосындысын айтады:
 (2.1.6)
(2.1.6)Математикалық үміт кездейсоқ шаманың мүмкін мәндерінің арифметикалық орташа мәніне жуықтап тең болады. Бұл математикалық үміттің ықтималдықтық мағынасы болып табылады.
Дискреттiк кездейсоқ шаманың
дисперсиясы деп, оның өзiнiң математикалық үмiтiнен ауытқуының квадратының математикалық үмiтiн айтады:
 (2.1.7)
(2.1.7)Дисперсия кездейсоқ шаманың мүмкін мәндерінің өзінің математикалық үмітінен қаншалықты алшақ жатқандығын сипаттайтын шама болып табылады.
Дисперсияны есептеудiң жеңiлдетiлген формуласы :
 (2.1.8)
(2.1.8) Дискреттiк кездейсоқ шаманың орташа квадраттық ауытқуы мына формуламен есептелiнедi:
Дискреттiк кездейсоқ шаманың к - реттi бастапқы моментi деп осы кездейсоқ шаманың к-шы дәрежесiнiң математикалық үмiтiн айтады:
 (2.1.9)
(2.1.9)Дискреттiк кездейсоқ шаманың к - реттi орталық моментi деп, оның өзiнiң математикалық үмiтiнен ауытқуының к-шы дәрежесiнiң математикалық үмiтiн айтады :
 (2.1.10)
(2.1.10)Кездейсоқ шаманың математикалық үмiтi бiрiншi бастапқы моментiне, ал дисперсиясы - екiншi орталық моментiне тең :
Сондай-ақ екiншi, үшiншi және төртiншi ретті орталық моменттер
бастапқы моменттер арқылы төмендегiдей өрнектеледi :
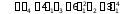 (2.1.11)
(2.1.11)Дискреттiк кездейсоқ шаманың ең ықтималды мәнiн оның Модасы (M0) деп атайды.
Айталық кездейсоқ шаманың n мүмкiн мәндерi болсын. Егер
теңдiгi орындалса, онда
Егер n=2к болса, онда
, егерде n=2к+1 болса, онда
Сондай-ақ қарастырылып отырған кездейсоқ шаманың үлестiрiм заңын қалыпты үлестiрiммен салыстыру үшiн Еk эксцесс және Аs асимметрия сипаттамалары қарастырылады. Мұнда
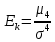 -3,
-3, 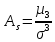
Ескерту : қалыпты үлестiрiм үшiн Ek = 0 , As = 0
Математикалық үмiттiң қасиеттерi
1. М(с) = с , 2. М(сх) = сМ(х)
3. М(х у) = М(х) М(у) 4. M(xy) = M(x)M(y)( мұнда Хжәне У тәуелсіз шамалар)
Дисперсияның қасиеттерi
1. D(x) 0 , 2. D(c) = 0
3. D(cx) = c2 D(x) 4. D(x y) = D(x) + D(y)
Мұндағы x және y тәуелсiз кездейсоқ шамалар.
Жоғарыда келтiрiлген үлестiрiм заңдарының математикалық үмiттерi мен дисперсияларын келтiрелiк.
1. Биномдық үлестiрiм
M(x) = np, D(x) = npq,
-
Пуассон үлестiрiмi
M(x) = , D(x) = ,
3. Геометриялық үлестiрiм
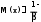 ,
, 4. Паскаль үлестiрiмi
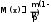 ,
, 5. Гипергеометриялық үлестiрiм
Мұнда m < 0,1N болғанда D(x) npq болады, яғни биномдық үлестiрiмнiң дисперсиясына жуықтап тең болады.
Сондықтан m < 0,1N болғанда

болады. Осы жағдайда
3-мысал. Дискреттiк кездейсоқ шама мына үлестiрiммен берiлсiн
| Х | -1 | 0 | 1 | 2 |
| р | 0,2 | 0,4 | 0,2 | 0,2 |