Сонымен a=1

Ендi F(x)- тi табалық:

x<0 болса

болса



болса

Cонымен


Математикалық үмiттi мына формула көмегiмен есептеймiз

М(x)=

Ендi дисперсияны есептеймiз

D(x)=

=[-x²cosx+2xsinx+2cosx]|

Ендi табалық. Ол ұшiн

= ;

яғни

Бұл ықтималдықты сондай-ақ интегралдық функцияны пайдаланып та табуға болатынын көрсетелiк:

=F( )-F(0)=(1-cos

---

)-(1-cos0)= .

7-мысал. Кездейсоқ шама дифференциалдық функциясы арқылы берiлген

f(x)=

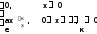
Табу керек;

1.Коэффициент а-ны;

2.Үлестiрiм функциясын;

3.[0; 1/к] аралықтан мән қабылдау ықтималдығын.

Шешуi: 1.Коэффициент а-ны табу үшiн үлестiрiм тығыздығының екiншiсi қасиетiн пайдаланамыз, яғни



немесе

1= =

яғни

Сонда f(x)=к²х , x>0

2. Бұл жерде үлестiрiм тығыздығының төртiншi қасиетiн пайдаланамыз.

Сонда

F(x)=

3. =F( )-F(0)=1-2e^-1.


ЕСЕПТЕР
115. Х- кездейсоқ шамасы бүкiл ОХ өсi бойынша мына үлестiрiм тығыздығымен , берiлген. Тұрақты параметр С-ны табу керек.

116. Х - кездейсоқ шамасы ОХ өсi бойында мына үлестiрiм функциясымен берiлген



Кездейсоқ шаманың мына [0;1] аралықтан мән қабылдайтындығының ықтималдығы қандай?

117. Х - кездейсоқ шама мына үлестiрiм тығыздығымен берiлген
а)f(x)= б)

M(x), D(x) - тердi табу керек.

118. Кездейсоқ шама үлестiрiм тығыздығымен берiлген

---

б)f(x)= б)

Белгiсiз коэффициент С-ны, интегралдық функцияны табыңыз.

119. Кездейсоқ шама дифференциалдық функциясы арқылы берiлген
а)f(x)= б)

Интегралдық функциясын және сандық сипаттамаларын табыңыз.

120. Кездейсоқ шама үлестiрiм тығыздығы арқылы берiлген
f(x)=

1. Интегралдық функциясын жазыңыз.

2.Кездейсоқ шаманың [2;4] аралықтан мән қабылдауының ықтималдығын табыңыз.

3.Төрт тәуелсiз сынақтарда осы кездейсоқ шаманың [1;2] интервалынан 4 рет мән қабылдауының ықтималдығын табыңыз.

121. Кездейсоқ шама үлестiрiм тығыздығымен берiлген.
а) б)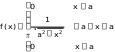
Интегралдық функциясын табыңыз.

122. Кездейсоқ шаманың интегралдық функциясы берiлген
а) б)

Кездейсоқ шаманың үлестірім тығыздығын, математикалық үмiтi M(x)-ті және дисперсиясы D(x)-ті табу керек

123. Кездейсоқ шама үлестiрiм функциясы арқылы берiлген


үлестiрiм тығыздығын табыңыз.

124. Кездейсоқ шама интегралдық функциясы арқылы берiлген
а) б)

---

Кездейсоқ шаманың [0,1] интервалдан мән қабылдау ықтималдығын, дифференциалдық фукциясын табыңыз.

125. Кездейсоқ шама үлестiрiм тығыздығы арқылы
б)

берiлген. Кездейсоқ шаманың үлестірім функциясын, математикалық үмiтi мен дисперсиясын табыңыз.

126.Кездейсоқ шаманың интегралдық функциясы берiлген
а) б)

a және b сандарын, үлестiрiм тығыздығын f(x)-ті табу керек.

127. 
     .Кездейсоқ шаманың интегралдық функциясы берiлген
     

а) б)

үлестiрiм тығыздығын f(x), математикалық үмiттi, дисперсияны және кездейсоқ шаманың [1;2] аралығында жату ықтималдығын табу керек.

128. 
     .Кездейсоқ шама интегралдық функциясы арқылы берiлген
     

а) б)

Тұрақты с - санын, математикалық үмiттi және дисперсияны табу керек.

129. 
     .Кездейсоқ шаманың интегралдық функциясы берiлген
     

а) б)

үлестiрiм тығыздығын f(x), математикалық үмiттi табу керек.

130. 
     .Кездейсоқ шаманың интегралдық функциясы берiлген
     

---

a - санын, ықтималдық тығыздығын f(x), математикалық үмiттi, дисперсияны және [0; 2] аралығынан мән қабылдау ықтималдығын табу керек.

131. 
     .Кездейсоқ шаманың интегралдық функциясы берiлген
     

Ықтималдық тығыздығын f(x), математикалық үмiттi және дисперсияны табу керек.

2. ҮЗІЛІССІЗ КЕЗДЕЙСОҚ ШАМАЛАРДЫҢ КЕЙБIР ҮЛЕСТIРIМ ЗАҢДАРЫ

1. 
   Бiрқалыпты үлестiрiм заңы
   

Анықтама. Егер Х - кездейсоқ шамасы [a,b] аралығында мән қабылдаса және оның үлестiрiм тығыздығы:
(2.2.12)

теңдiгi арқылы анықталса, онда ол кездейсоқ шама бiрқалыпты үлестiрiм заңымен берiлген дейдi.

Бұл үлестiрiм заңдылығы үшiн
, (2.2.13)

Интегралдық функциясы

(2.2.14)

Берiлген аралықтан [c; d] мән қабылдау ықтималдығы
(2.2.15)
8-мысал. Кездейсоқ шама дифференциалдық функциясы арқылы берiлген


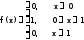
Интегралдық функцияны табыңыз. M(x), D(x)- тарды есептеңiз.

Шешуi: Есептiң шарты бойынша [0;1] аралығында f(x)=1 яғни тұрақты. Сондықтан бұл кездейсоқ шама бiрқалыпты үлестiрiм заңымен берiлген. Мұнда a=0, b=1

.

Олай болса

---

Смотрите также файлы

• Программа среднего профессионального образования 40. 02. 01 Право и организация социального обеспечения Дисциплина Физическая культура (2 семестр) Практическое задание 7.doc

• Родной язык Вопросы к промежуточной аттестации.docx

• Все чаще в современном обществе на различных уровнях затрагивается проблема ухудшения состояния здоровья нации.docx

• Влияние вредных привычек на организм человека.odt

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx