Х	0	1	3	3,5
Р	0,1	0,4	0,2	0,3

Х - тiң үлестiрiм функциясын табыңыз.

Шешуi: Ол үшiн (2.2.2) формуласын пайдаланамыз. Кестеден байқағанымыздай х<0 болса, онда X-тiң қабылдайтын мүмкiн мәндерi жоқ. Ал 0  x <1 болғанда Х-тiң қабылдайтын бiр мәнi, ол - 0; ендi 1  x <3 болса, онда Х-тiң қабылдайтын екi мәнi бар, ол 0;1; т.с.с. ақырында х  3,5 болса, онда Х өзiнiң барлық мұмкiн мәндерiн қабылдайды, ол - 0; 1; 3; 3,5.

Ендi (2.2.2) формуласына түсiнiк келтiрелiк. Жоғарыда айтқанымыздай х<0 болса, онда есептiң шарты бойынша 0-санының сол жағында берiлген кездейсоқ шаманың ешбiр мүмкiн мәнi жоқ, яғни кездейсоқ шаманың өзiнiң мүмкiн мәндерiнiң бiреуiн қабылдауын оқиға екенiн ескерсек, онда оның 0-санының сол жағынан мән қабылдауы мүмкiн емес оқиға, олай болса

F(x) = P(x<0) = 0

Ендi x<1 болса,онда 1- санының сол жағында есептiң шарты бойынша кездейсоқ шаманың бiр мәнi бар, ол 0 - саны. Олай болса

F(x)=P(x<1)=P(x=0)=0,1

Сол сияқты x<3 болғанда, 3-санының сол жағында кездейсоқ шаманың екi мәнi бар. Ол осы мәндердiң бiреуiн қабылдауы мүмкiн, яғни екi оқиғаның бiреуi пайда болады дегенiмiз. Сондай-ақ, бұл екi оқиға үйлесiмсiз, сондықтан үйлесiмсiз оқиғалардың қосындысының ықтималдығы туралы теореманы пайдаланып:

F(x)=P(x<3)=P(x=0)+P(x=1)=0,1+0,4=0,5

Осы жолмен x<3,5 болғанда және x>3,5 болғандағы F(x)-ның мәндерiн есептеуге болады.

Сонымен қорытындысында:



Ендi F(x) функциясының графигiн тұрғызайық.




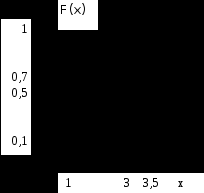
2-мысал. Кездейсоқ шама интегралдық функциямен берiлген

Үлестiрiм кестесiн құрыңыз, М(X), D(X), табыңыз.

Шешуi: Интегралдық функцияның өрнегiнен байқағанымыздай x<-2, болғанда F(x)=0, яғни -2 -нiң сол жағында кездейсоқ шаманың мүмкiн мәндерi жоқ. Ал x<-1 болғанда F(x)=0,1 бұл жағдайда кездейсоқ шаманың бiр мүмкiн мәнi бар ол - 2, сол сияқты x<1 болғанда F(x)=0,4, яғни 1 санының сол жағында кездейсоқ шаманың екi мүмкiн мәнi бар, олар - 2; 1.

---

Сондықтан F(x)=P(x=-2)+P(x=-1). Мұнда P(x=-1)=0,3.

Ойымызды осылай жалғастыра отырып ақырында мынадай үлестiрiм кестесiн аламыз:

Х	-2	-1	1	2
Р	0,1	0,3	0,5	0,1

М(X)=0,2, D(X)=1,56, =1,25.
ЕСЕПТЕР
112. Жоғарыда келтiрiлген 84 және 90 есептердегi қарастырған кездейсоқ шамалардың интегралдық функцияларын табыңыз. Сандық сипаттамаларын есептеңiз.

113. Кездейсоқ шама интегралдық функциясы арқылы берiлген

а) б)

Үлестiрiм кестесiн табыңыз.

114. Тиынды екi рет лақтырғанда елтаңбаның пайда болуының үлестiрiм кестесiн жазыңыз. Интегралдық функциясын табыңыз.
1.ҮЗIЛIССIЗ КЕЗДЕЙСОҚ ШАМАЛАРДЫҢ САНДЫҚ

СИПАТТАМАЛАРЫ

1. Математикалық үмiтi

(2.2.4)

2. Дисперсиясы

(2.2.5)

Дисперсияның жеңiлдетiлген формуласы:
(2.2.6)

3. Орташа квадраттық ауытқуы
(2.2.7)

4. К - реттi бастапқы моментi
(2.2.8)

5. К - реттi орталық моментi
(2.2.9)
Үзiлiссiз кездейсоқ шамалардың мүмкiн мәндерi жөнiнде белгiлi дәрежеде ақпарат беретiн басқада сипаттамалар бар. Оларға мода, медиана, асимметрия, эксцесстер жатады.

Анықтама. Егер кездейсоқ шаманың белгiлi бiр М₀ мәнiнде

---

теңдiгi орындалса, онда M₀ кездейсоқ шаманың модасы деп аталады.

Анықтама. Егер кездейсоқ шаманың белгiлi бiр M_D мәнiнде

Р(x< M_D)=P(x> M_D) орындалса, онда M_D кездейсоқ шаманың медианасы деп аталады.

Анықтама. Кездейсоқ шаманың өзiнiң математикалық үмiтi бойынша симметриядан ауыткуы, оның асимметриясы деп аталады және Аs деп белгiлейдi:

Аs=₃/ ³ (2.2.10)
Мұнда ₃ -үшiншi реттi орталық момент, - орташа квадраттық ауыткуы.

Егер кездейсоқ шаманың үлестiрiмi математикалық үмiтi бойынша симметриялы болса, онда As=0. Егер As>0 болса, онда дифференциалдық функцияның графигi оң жаққа қарай "созыңқы" болады, ал As<0, онда - сол жаққа қарай "созыңқы" болады.

Анықтама. Қалыпты үлестiрiммен салыстырғанда дифференциалдық функцияның графигiнiң "жатыңқылық" деңгейiн анықтайтын шаманы эксцесс деп атайды және арқылы белгiлейдi: (2.2.11)

Мұнда қалыпты үлестiрiм үшiн . Егер , онда Гаусс қисығымен салыстырғанда график "көтерiңкi" болады, егер , онда график "жатыңқы"

болады.

3-мысал. Үзiлiссiз кездейсоқ шама дифференциалдық функциямен берiлген



Кездейсоқ шаманың Мо, М_D, As, Eк -ларын табу керек.

Шешуi: 1. Моданы табу үшiн f(x) функциясының максимумын табамыз. Ол үшiн әуелi бiрiншi туындыны тауып оны нөлге теңеп, сосын кризистiк нүкте тауып f(x)-тiң максимумын белгiлi схема бойынша анықтаймыз:

, ,

---

, ,

Мұнда [0; ] кесiндiсiнде тек x= мәнi жатады. Ендi

• 
  ( )=- <0. Осыдан . Олай болса Mo= .
  

Ендi медиананы табалық. Анықтамадан



Осыдан



Сондай-ақ,



Осыдан

Ендi As және Eк-ларды табу үшiн әуелi

, , ,

табамыз.
Сонда

, ,
Осы есептеулердi пайдаланып Аs=0 екенiн көремiз, яғни f(x) функциясының графигi өзiнiң M(x)-i бойынша симметриялы орналасқан.
Сол сияқты

---

екенiн көремiз, яғни f(x)-тiң графигi Гаусс кисығына қарағанда "жатыңқы" болады екен.

4-мысал. Кездейсоқ шама дифференциалдық функциясы арқылы берiлген


f(x)=

Интегралдық функциясын табыңыз.
Шешуi: Дифференциалдық функцияның төртiншi қасиетi бойынша

F(x)=

Осыдан x0 болғанда f(x)=0 болатынын пайдаланып

F(x)= =0

Ендi 0 сондықтан

F(x)=

Ақырында x>3 болғанда f(x)=0 осыдан

F(x)=

Сонымен

F(x)=

5-мысал. Үзiлiссiз кездейсоқ шама үлестiрiм функциясымен берiлген

F(x)=

1.Үлестiрiм тығыздығын табу керек

1.М(x), D(x) табу керек

2.Мына интервалдан [ 0,5;1] мән қабылдауының ықтималдығын табу керек.

Шешуi:

1. f(x)=

2. M(X)=

D(X)=

3.

6-мысал. Кездейсоқ шама дифференциалдық функция арқылы берiлген

f(x)=

Табу керек: a, F(x), M(x), D(x), P(0
Шешуi: а коэффициентiн табу үшiн дифференциалдық функцияның қасиетiн пайдаланамыз:



Есептiң шарты бойынша

1= =

---

Смотрите также файлы

• Программа среднего профессионального образования 40. 02. 01 Право и организация социального обеспечения Дисциплина Физическая культура (2 семестр) Практическое задание 7.doc

• Родной язык Вопросы к промежуточной аттестации.docx

• Все чаще в современном обществе на различных уровнях затрагивается проблема ухудшения состояния здоровья нации.docx

• Влияние вредных привычек на организм человека.odt

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx