Файл: Ытималдытар теориясы жне математикалы статистика i тарау. Кездейсо оиалар негізгі тсініктер. Оиаларды трлері.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 773
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
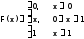
M(x)=
9-мысал. Автобустың аялдамаға келу интервалы 10 мин. Кездейсоқ шама - автобусты күту уақыты. Осы кездейсоқ шаманың дифференциалдық және интегралдық функцияларын жазыңыз.
Шешуi: Есептiң шарты бойынша а=0, b=10. Сондықтан,

Ендi интегралдық функцияны табалық:

Е С Е П Т Е Р
132. Кездейсоқ шама бiрқалыпты үлестiрiммен берiлген. Оның үлестiрiм тығыздығы

коэффициентт А -ны табыңыз. Дисперсиясын есептеңiз.
133. Кездейсоқ шама бiрқалыпты үлестiрiммен сипатталады. Оның интегралдық функциясы

түрiнде берiлген. Кездейсоқ шаманың дифференциалдық функциясын анықтаңыз. Мына [4;9] интервалынан мән қабылдау ықтималдығын табыңыз.
134. Х - кездейсоқ шамасы мына [2; 8] интервалда бiрқалыпты үлестiрiммен берiлген. Математикалық үмiттi табыңыз.
-
Көрсеткiштiк үлестiрiм заңы
Анықтама. Егер Х-кездейсоқ шамасы мына үлестiрiм тығыздығы
 (2.2.16)
(2.2.16)aрқылы берiлсе, онда ол көрсеткiштiк үлестiрiм заңымен берiлген дейдi.
Интегралдық функциясы
 (2.2.17)
(2.2.17) Бұл үлестiрiмнiң сандық сипаттамалары:
M(x)=
,
Кездейсоқ шаманың
10-мысал. Кездейсоқ шама интегралдық функциясы арқылы берiлген

Математикалық үмiттi, дисперсияны табыңыз.
Шешуi: Әуелi үлестiрiм тығыздығын табамыз

Бұдан M(x)=
ЕСЕПТЕР
135. Телевизорды жөндеуге жұмсалатын уақыт кездейсоқ шама. Осы кездейсоқ шаманың интегралдық функциясы.

түрiнде берiлген. Оның математикалық үмiтiн, дисперсиясын анықтаңыз.
136. Кездейсоқ шама өзiнiң дифференциалдық функциясы арқылы берiлген

кездейсоқ шаманың өзiнiң математикалық үмiтiнен кем мән қабылдауының ықтималдығын табыңыз.
137. Су түбiндегi кеменi iздеп табу уақыты кездейсоқ шама. Кеменi t уақытында iздеп табу ықтималдығы
P(t)=1-e-t, >0;
кеменi iздеп табуға қажеттi орташа уақытты табыңыз.
Нұсқау: Берiлген P(t) функциясын кездейсоқ шаманың интегралдық функция ретiнде қарастыру керек.
138. Үзiлiссiз кездейсоқ шама көрсеткiштi үлестiрiммен берiлген

Тәжiрибе кезiнде осы кездейсоқ шаманың [1;2] интервалынан мән
қабылдауының ықтималдығын табу керек.
139. Кездейсоқ шама көрсеткiштi үлестiрiммен берiлген

сандық сипаттамаларын табыңыз.
-
Қалыпты үлестiрiм заңы
Анықтама. Егер Х - кездейсоқ шамасы мына үлестiрiм тығыздығы
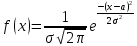 (2.2.20)
(2.2.20)арқылы берiлсе, онда ол қалыпты үлестiрiм заңымен берiлген дейдi.
Мұнда
M(x)=a, D(x)=2, AS=0, Ek=0 (2.2.21)
Сондай-ақ
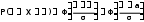 (2.2.22)
(2.2.22)қалыпты үлестiрiммен берiлген кездейсоқ шаманың берiлген интервалдан мән қабылдауының ықтималдығы, Ф(х) - Лаплас функциясы. Мына формула
кездейсоқ шаманың өзiнiң математикалық үмiтiнен ауыткуының абсолют шамасы - дан кiшi болуының ықтималдығын анықтайды.
Егер формулада =3 болса, онда
немесе
яғни кездейсоқ шаманың өзiнiң математикалық үмiтiнен ауыткуының абсолют шамасы 3 - дан аспауының ықтималдығы бiрге өте жақын екенiн көрсетедi.
Осыдан үш сигма ережесi шығады:
Егер кездейсоқ шама қалыпты үлестiрiммен берiлсе, онда оның математикалық үмiттен ауытқуының абсолют шамасы үш орташа квадраттық ауытқудан аспайды.
11-мысал. Станок-автомат ұзындығы 125 мм деталдар дайындайды. Олардың берiлген ұзындықтан ауыткуы 0,5 мм аспайды. Дайындалған деталдардың 7 процентi сапасыз. Деталь ұзындықтарын кездейсоқ шама ретiнде қарастырып және оны қалыпты үлестiрiм арқылы берiлген деп оның дисперсиясын табу керек.
Шешуi: Х-кездейсоқ шама-деталдар ұзындығы. Есептiң шарты бойынша деталдардың орташа ұзындығы 125 мм, олай болса М(х)=а=125 мм. Сондай-ақ дайындау кезiнде 124,5
Есептiң шарты бойынша 7 процент деталдар сапасыз. Олай болса
яғни 0,93 ықтималдықпен сапалы деталдар дайындалады.
Ф(х)- функциясының кестесiнен
аламыз.
Осыдан 2=D(x)=0,078
12-мысал. Кездейсоқ шама қалыпты үлестiрiммен берiлген және M(x)=30, D(x)=4. Mына теңсiздiктiң |x-30|< ықтималдығы 0,8-ге тең болғанда қандай болу керек?
Шешуi: Есептiң шарты бойынша
Осыдан
Кестеден
13-мысал. Кездейсоқ шама қалыпты үлестiрiм арқылы берiлген. Математикалық үмiтi M(x)=5 дисперсиясы D(x)=0,64. Дифференциалдық функциясын жазыңыз. Мына [4; 7] интервалдан мән қабылдауының ықтималдығын табыңыз.
Шешуi: Есептiң шарты бойынша M(x)=5, D(x)=0,64, яғни =0,8.
Сондықтан
=
14-мысал. Айталық дайындалған бөлшектiң бiр өлшемi қалыпты үлестiрiммен берiлген кездейсоқ шама болсын, математикалық үмiтi a=10см, ал =0,01. 1) Кездейсоқ шаманың өзiнiң математикалық үмiтiнен ауытқуы 0,025 артпауының ықтималдығын табыңыз; 2)Дайындалған бөлшектiң өлшемi 10,03 сантиметрден артпайтындығының ықтималдығын табыңыз; 3) Кездейсоқ шаманың өзiнiң математикалық үмiтiнен ауытқуының абсолют шамасы 0,02-тен артпауының ықтималдығы 0,99-ға тең болуы үшiн бөлшектiң дайындалуының дәлдiгiн сипаттайтын қандай болуы керек?
Шешуi: 1.
2. P
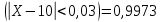
Бұл жерде «үш сигма» ережесі қолданылған.
3.
сонда кестеден
осыдан =0,0077.
ЕСЕПТЕР
140. Кездейсоқ шама дифференциалдық функция арқылы берiлген
а) коэффициент С-ны табыңыз б) f(x) функциясының графигiн салыңыз.
141. Кездейсоқ шама қалыпты үлестiрiммен берiлген. Математикалық үмiтi M(x)=2 орташа квадраттық ауытқуы =1. Кездейсоқ шаманың [4,7] интервалдан мән қабылдауының ықтималдығын табыңыз.
142. Дайындалған деталдардың ұзындығы стандарттан ауытқуы қалыпты үлестiрiммен берiлген. Деталдың стандартты ұзындығы (математикалық үмiтi) a=40 см. Орташа квадраттық ауытқуы 0,4 см. Стандартты ұзындықтан ауытқуының абсолют шамасы 0,6 сантиметрден аспайтындығының ықтималдығын табыңыз.
143. Берiлген партияда алманың салмағы кездейсоқ шама болып, ол қалыпты үлестiрiм арқылы берiлген болсын және M(x)=140 г.,
1.Осы партиядан алынған кез-келген алманың салмағы 124 граммнан 148 граммға дейiн болатындығының ықтималдығы қандай?
2.Алынған алманың салмағы орташа салмақтан /a=140 гр/ ауытқуы + 8 граммнан аспайтындығының ықтималдығын табу керек.
144. Зауытта жасалған бөлшектiң диаметрi қалыпты үлестiрiммен берiлген кездейсоқ шама. Диаметрдiң стандартты ұзындығы a=2,5 см, ал орташа квадраттық ауытқуы = 0,01. Егер ақиқат оқиға ретiнде ықтималдығы 0,9973-ке тең оқиғаны қарастырсақ, диаметрдiң ұзындығы қандай аралықта жатуы керек?
145.Зауыт диаметрi d0 = 5 мм шариктер даярлайды. Даярлау кезiнде диаметрi берiлген ұзындықтан ауытқуы кездейсоқ шама, ол қалыпты үлестiрiммен берiлген және орташа квадраттық ауытқуы = 0,01. Бақылау кезiнде диаметрi берiлген ұзындықтан 0,02 мм ауытқыған шариктер қабылданбайды. Бақылау кезiнде қанша процент шариктер қабылданбайды?
146. Кездейсоқ шама Х қалыпты үлестiрiммен берiлген, математикалық үмiтi а, орташа квадраттық ауытқуы . Берiлген (,) интервалында осы қалыпты үлестiрiмдi жуықтап бiрқалыпты үлестiрiммен ауыстыру керек. Бiрақта кездейсоқ шаманың берiлген сандық сапаттамалары өзгермей сақталатын болсын.
Нұсқау: Берiлген сандық сипаттамалар сақталу үшiн қалыпты үлестiрiммен бiрқалыпты үлестiрiмнiң сәйкес сандық сипаттамаларын теңестiру арқылы және сандарын анықтау қажет.
147. Кездейсоқ шама Х қалыпты үлестiрiммен берiлген. Математикалық үмiтi а, орташа квадраттық ауытқуы . f(x) функциясының графигiнiң иiлу нүктелерiнiң координаталарын анықтаңыз.
148. Қалыпты үлестiрiммен берiлген кездейсоқ шаманың математикалық үмiтi a=0, ал (-b;b) аралықтан мән қабылдау ықтималдығы 0,5. Орташа квадраттық ауытқуын тауып үлестiрiм тығыздығын жаз.