1.Х және У кездейсоқ шамалардың үлестiрiм заңдарын жазыңыз.

2.а) Х-тiң У=y₃ болғандағы шартты үлестiрiм заңын жазыңыз;

б) У-тiң Х=х₂ болғандағы шартты үлестiрiм заңын жазыңыз;

3.Х пен У өзара тәуелсiз бе?

4.Үлестiрiм функциясын F(x,y) табыңыз:

Бiр өлшемдi Х және У кездейсоқ шамалардың үлестiрiм F₁(x) және F₂(y) функияларын жазыңыз.

5.Корреляциялық коэффициенттi табыңыз.

6.Шартты математикалық үмiттерiн табыңыз.
Шешуi: 1. кестеден Х және У кездейсоқ шамаларының үлестiрiм заңдары төмендегiдей түрде жазылады
2 кесте 3 кесте

Х	-2	3			У	-1	0	1
Рх	0,7	0,3			Ру	0,33	0,24	0,43

2. а) Х - тiң У=у₃ болғандағы шартты үлестiрiм заңын жазу үшiн әуелi

, - тердi табамыз:



Сонда мына үлестiрiм заңын аламыз:

4 кесте

Х	-2	3
Р(Х/У=y3)	32 43	11 43

б) У - тiң Х=х₂ болғандағы шартты үлестiрiм заңын осылай есептесек:

5 кесте

У	-1	0	1
Р(У/Х=х2)	12 30	7 30	11 30

3.Х және У тәуелсiз бе?

Екi Х және У кездейсоқ шамалардың өзара тәуелсiздiгiн анықтау үшiн олардың сәйкес шартты және шартсыз үлестiрiм заңдарын салыстыру керек. Егер ол заңдар бiрдей кестелермен берiлсе, онда олар тәуелсiз болғаны, ал егер ол кестелер бiрдей болмаса, онда олар тәуелдi болғаны. Сондықтан бiз № 2; № 4 және №3; №5 кестелердi өзара салыстырсақ, олардың бiрдей еместiгiн байқаймыз, олай болса Х және У өзара тәуелдi кездейсоқ шамалар болады.

---

4.Үлестiрiм функциясын (2.3.3) формуланы пайдаланып жазамыз


Ендi F₁(x) және F₂(y) функцияларын 2 кесте мен 3 кестенi пайдаланып табамыз:
.

5.Корреляциялық коэффициенттi


формуласын пайдаланып табалық.

Әуелi М(х) және М(у) - тердi 2 - 3 кестелердi пайдаланып табамыз.

М(х) = -20,7+30,3=-0,5, D(х)=5,25,

M(y)=-10,33+00,24+10,43=0,1, D(y)=0,87,



Сонда

.

Осыдан екенiн көремiз, яғни Х және У өзара тәуелдi кездейсоқ шамалар болады.

6. Айталық М(Х/У=y₃) және М(У/Х=х₂) табу керек болсын. Оларды табу үшiн 4- 5 кестелердi пайдаланамыз. Сонда



.

2-мысал. Өзара тәуелсiз Х және У кездейсоқ шамалар сәйкес [а,b] және [c,d] аралықтарында бiрқалыпты үлестiрiм заңдарымен берiлген. Табу керек: 1. f₁(x), f₂(y) үлестiрiм тығыздықтарын; 2. (X,У) системасының f(x,y) үлестiрiм тығыздығын; 3. Х және У кездейсоқ шамаларының F₁(x) және F₂(у) үлестiрiм функцияларын; 4. (Х,У) жүйесінің F(x,y) үлестiрiм функциясын; 5. x₁,x₂ [a,b] және у₁,у₂ [с,d] болғанда P(x₁2, y₁<У2) табу керек.

Шешуi: Бiрқалыпты үлестiрiмнiң анықтамасы бойынша

1.


2.Х және У тәуелсiз болғандықтан

осыдан


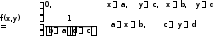
3.



4.Х және У тәуелсiз болғандықтан F(x,y)=F₁(x)F₂(y),

осыдан



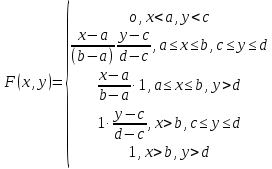
5.Үлестiрiм функциясының бесiншi қасиетi бойынша
P(x₁Xx₂, y₁Уy₂)= [F(x₂, y₂)-F(x₁, y₂)] - [F(x₂, y₁)-F(x₁, y₁)]
3-мысал. Екi кездейсоқ Х және У шамалар системасы үлестiрiм функциясымен берiлген



үлестiрiм тығыздықтары және F₁(x),F₂(y)- тарды тап.

Шешуi:

1.

2.


3.

4.

ЕСЕПТЕР
167. Х және У кездейсоқ шамалардың жүйесінің үлестiрiм заңы кесте арқылы берiлген

Y X	0	1	2	3
1	0,04	0,05	0,01	0,06
4	0,24	0,15	0,04	0,07
6	0,05	0,10	0,09	0,10

Табу керек:

1.Х және У -тердiң әрқайсысының үлестiрiм заңдарын;

2.Х=х₂=4 болғандағы У-тiң шартты үлестiрiм заңын;

3.Х пен У тәуелдi ме?

4.P(x<4,y<2)=?

5.Корреляциялық коэффициенттi r_xy.

168. 
     Х және У кездейсоқ шамалар жүйесінің үлестiрiм заңы кесте арқылы берiлген.
     

Х У	-1	0	1
0	0	0,2	0,1
1	0,4	0,1	0,2

Табу керек: 1. Х және У -тердiң әрқайсысының үлестiрiм заңдарын;

2.У=1 болғанда Х-тiң шартты үлестiрiм заңын; 3.Х пен У тәуелдi ме? 4.Корреляция коэфициентін.

169.Екi атқыш бiр нысанаға бiр бiрiнен тәуелсiз екi атыс жасады. Бiрiншiсiнiң нысанаға тигiзу ықтималдығы 0,8, екiншiсiнiкi - 0,6. Айталық Х- бiрiншi атқыштың нысанаға тигiзген оқтарының саны, У - екiншi атқыштың тигiзген оқтарының саны. Табу керек: 1. Х және У кездейсоқ шамаларының жүйесінің үлестiрiм заңын; 2. Х және У - тердiң әрқайсысының үлестiрiм заңдарын; 3.Х пен У тәуелдi ме? 4.Корреляция коэфициентін.

170. Жәшiкке бiрдей 5 қызыл 2 жасыл және 3 көк шарлар салынған. Жәшiктен 3 шар алынды. Айталық Х-алынған қызыл шарлар саны, У - алынған жасыл шарлар саны болсын. Табу керек: 1. Х пен У -тердiң үлестiрiм заңдарын; 2. (Х,У) жүйесінің үлестiрiм заңы; 3. r_xy -ті тап.4.Х пен У теуелді ме?

171. Х және У тәуелсiз кездейсоқ шамалар сәйкес [4;6] және [0;3] аралықтарында бiрқалыпты үлестiрiммен берiлген.

Табу керек: 1. - тердi; 2. - тердi; 3. (X,У) жүйесінің үлестiрiм тығыздығын; 4. - тi;

5. 
   P(5

172. (Х,У) жүйесі үлестiрiм функциясы арқылы берiлген


Табу керек: 1. - үлестiрiм тығыздығын;

2. Және - функцияларын.

3. 
   
   

173. №167 есептегі М(Х/ У=2) , М(У/Х=1) шартты математикалық үміттерді тап.

174. . №168 есептегі М(Х/ У=-1) , М(У/Х=1) шартты математикалық үміттерді тап.

---

§4. КЕЗДЕЙСОҚ ШАМАЛАР ФУНКЦИЯСЫ

Кездейсоқ шамалар Х₁,Х₂, ..., Х_n жүйесін қарастыралық. Олардың әрқайсысының үлестiрiм заңдары белгiлi болсын. Сонда кездейсоқ шамалар функциясы мына түрде берiледi

y= (x₁, x₂, ..., x_n) (2.4.1)

Осы кездейсоқ шама У- тiң үлестiрiм заңын табу керек. Бiр кездейсоқ шаманың функциясын қарастыралық:

y=(x) (2.4.2)

Мұнда Х дискреттiк немесе үзiлiссiз кездейсоқ шама болуы мүмкiн.

1. 
   Х - дискреттiк кездейсоқ шама үлестiрiм кестесiмен берiлген.
   

Х	x1	x2	...	xn
P	p1	p2	...	Pn

Сонда У - кездейсоқ шамасының үлестiрiм заңы

y	(x1)	(x2)	...	(xn)
P	p1	p2	...	Pn

2.Х - үзiлiссiз кездейсоқ шама f(x) үлестiрiм тығыздығымен берiлген, сонда У - кездейсоқ шаманың үлестiрiм заңын жазу үшiн оның g(y) үлестiрiм тығыздығын табу керек. Екi жағдай болуы мүмкiн:

1. (x) функциясы [a,b] аралығында монотонды-өспелi үзiлiссiз және дифференциалданатын функция. Онда осы аралықта оның бiр ғана x=(y) керi функциясы бар болады да

g(y)=f((y))| '(y)| (2.4.3)

орындалады.

2. y= (x) функциясы монотонды емес.

Сондықтан оның x₁=₁(y), x₁=₂(y),..., x_n=_n(y) керi функциялары болады да

g(y)= (2.4.4)

орындалады.

1-мысал. Кездейсоқ шама үлестiрiм кестесiмен берiлген

X	0	1	2	3
p	0,1	0,2	0,3	0,4

---

y=(4-x)cosx кездейсоқ шамасының үлестiрiм кестесiн табыңыз.

Шешуi: Әуелi y - тiң мүмкiн мәндерiн анықталық:

Y₁=(4-0)cos0=4, y₂=y(1)=-3,

y₃=y(2)=2, y₄=y(3)=-1

Сонымен

y	-3	-1	2	4
q	q1	q2	Q3	q4

кестесiн алдық.

Ендi q_i - лердi табалық.

q₁=p(y=-3)=p(x=1)=0,2

q₂=p(y=-1)=p(x=3)=0,4

q₃=p(y=2)=p(x=2)=0,3

q₄=p(y=4)=p(x=0)=0,1

Сөйтiп, ақырында

y	-3	-1	2	4
q	0,2	0,4	0,3	0,1

үлестiрiм кестесiн алдық.

2-мысал. Кездейсоқ шама үлестiрiм тығыздығымен берiлген



y=x³ кездейсоқ шаманың үлестiрiм тығыздығын тап.

Шешуi: y=x³ функциясы монотонды-өспелi, үзiлiссiз және дифференциалданатын функция. Сондықтан оның керi функциясы x= болады. Осыдан (2.4.3) формуланы пайдаланып аламыз


3-мысал. Екi мерген бiр-бiрiнен тәуелсiз нысанаға сәйкес 2 және 3 атыс жасайды. Бiрiншiсiнiң нысанаға тигiзу ықтималдығы 0,9, ал екiншiсiнiкi - 0,8. X,Y - бiрiншi және екiншi мергеннiң нысанаға тигiзулерiнiң сандары. Z=X+Y, Z=XY кездейсоқ шамалардың үлестiрiм кестесiн жазыңыз. М(Х+У), М(XУ) - тердi табыңыз.

Шешуi: Х және У кездейсоқ шамалар биномдық үлестiрiм заңымен берiлген. Сондықтан Бернулли формуласын пайдаланып

Х	0	1	2		У	0	1	2	3
Р	0,01	0,18	0,81		Р	0,08	0,096	0,384	0,512

---

үлестiрiм кестелерiн аламыз.

Екі кездейсоқ шамалардың қосындысы көбейтіндісі Х+ У ( ХУ) деп мүмкін мәндері x_i+y_{j (} x_iy_j ) және сәйкес ықтималдықтары р_i р¹ _j

болатын кездейсоқ шаманы айтады.

Ендi Z=X+Y, Z= XY кездейсоқ шамаларының мүмкiн мәндерiн x_i+y_j және x_iy_j табалық. Олардың ықтималдықтары P(X=x_i)P(У=y_j) арқылы есептеледi. Ендi x_i+y_j және x_iy_j мүмкiн мәндерiн есептелiк.

x+y	0	1	2	3	4	5
P	0,0008	0,01464	0,07296	0,09368	0,4032	0,41472

xy	0	1	2	3	4	6
P	0,08920	0,00432	0,08856	0,09216	0,31104	0,41472

үлестiрiм заңдарын аламыз.

Сондай-ақ M(x+y)=4,128 M(xy)=4,1904

Математикалық статистикада тәуелсiз қалыпты үлестiрiммен берiлген кездейсоқ шамалардың функциясы болып келетiн үлестiрiм заңдарымен берiлген кездейсоқ шамалар қарастырылады. Солардың жиi кездесетiн үшеуiн төменде қарастырамыз.

1. Xu - квадрат үлестiрiм (²- үлестiрiм). Айталық Х₁, Х₂, ..., Х_- тәуелсiз қалыпты үлестіріммен берілген кездейсоқ шамалар болсын және a=0, =1 болсын.

Ендi

²_= x₁²+ x₂²+...+ x_²

кездейсоқ шаманы қарастыралық.

Бұл кездейсоқ шаманың үлестiрiм заңы ² - үлестiрiм деп аталады. Мұнда  - еркiндiк дәрежелер саны деп аталады.

Жалпы жағдайда x_к(к= ) қалыпты үлестiрiм беріліп және параметрлерi a,  болса, онда алмастыруы арқылы параметрлерi (0,1) болатын қалыпты үлестiрiмге келтiруге болады, яғни

²_=

---

Смотрите также файлы

• Программа среднего профессионального образования 40. 02. 01 Право и организация социального обеспечения Дисциплина Физическая культура (2 семестр) Практическое задание 7.doc

• Родной язык Вопросы к промежуточной аттестации.docx

• Все чаще в современном обществе на различных уровнях затрагивается проблема ухудшения состояния здоровья нации.docx

• Влияние вредных привычек на организм человека.odt

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx