Шешуi: Жоғарғы сортпен шығарылған бұйымдар саны кездейсоқ шама. Оны Х арқылы белгiлейiк. Бұл кездейсоқ шама биномдық үлестiрiммен берiлген. М(х) осы кездейсоқ шаманың математикалық үмiтi. Есептiң шарты бойынша n=100000, P=0,75, q=0,25.
Сонда

М(х)=1000000,75=75000, D(x)=18750

Осыдан



яғни


ЕСЕПТЕР

179. 
     .Дискреттiк кездейсоқ шама үлестiрiм заңдарымен берiлген
     

x	1	2
p	0,8	0,2

1.Мына |Х-M(x)|<1 теңсiздiгiнiң орындалуының ықтималдығын

табыңыз.

2.Чебышев теңсiздiгiн пайдаланып |Х-M(x)|<1 теңсiздiгiнiң

орындалуының ықтималдығын бағалаңыз.

180. Детальдiң орташа ұзындығы а=50 см, ал дисперсиясы ²= 0,1. Чебышев теңсiздiгiн пайдаланып алынған кез келген детальдiң ұзындығы 49,5 сантиметрден 50,5 см аралығында болатынының ықтималдығын бағалаңыз.

181. Кез келген кездейсоқ шаманың өзiнiң математикалық үмiтiнен ауытқуының абсолют шамасы үш орташа квадраттық ауытқудан артпауының ықтималдығын бағалаңыз.

182. Жарамсыз радиошам жасап шығару ықтималдығы 0,25. Бiр партияда 1000 радиошам болса, жарамсыз радиошамдардың саны 250-ден ауытқуының абсолют шамасы 40-тан кем болуының ықтималдығын бағалаңыз.

183.Дискреттiк кездейсоқ шама үлестiрiм кестесiмен берiлген

Х	0,3	0,6
p	0,2	0,8

|X-M(x)|<0,2 теңсiздiгiнiң орындалу ықтималдығын бағалаңыз.

184. Елдi мекенде судың сөткелiк шығыны кездейсоқ шама. Оның орташа квадраттық ауытқуы 10000 л. Осы елдi мекенде бiр күн iшiнде су шығынының математикалық үмiттен ауытқуының абсолют шамасы 25000 литрден кем болмауының ықтималдығын бағалаңыз.

185. Әрбiр сынақта А оқиғасының пайда болу ықтималдығы 0,5. Чебышев теңсiздiгiн пайдаланып 100 сынақта А оқиғасының 40-тан 60-қа дейiнгi аралықта пайда болуының ықтималдығын бағалаңыз.

186.Кездейсоқ шама үлестiрiм кестесiмен берiлген

Х	1	2	3	4	5	6
Р	0,05	0,1	0,25	0,3	0,2	0,1

---

Мына теңсiздiктiң |X-M(x)|<2 орындалуының ықтималдығын бағалаңыз.

187.Белгiлi бiр прибор тәуелсiз жұмыс iстейтiн 10 элементтен тұрады. Т уақыт iшiнде әр элементтiң жұмыс iстемей қалу ықтималдығы 0,5. Т уақыт iшiнде жұмыс iстемей қалған элементтер мен осы жұмыс iстемей қалған элементтердiң орташа санының (математикалық үмiтi) айырмасының абсолют шамасының:

1)екiден кем болуының,

2) екiден кем болмауының ықтималдықтарын бағалаңыз.

188. Зауытта стандартқа жатпайтын радиошамдар шығару ықтималдығы 0,25. Шығарылған 2000 радиошамдардың iшiнде стандартқа жатпайтын шамдар санының 500-ден айырмасы 75-тен кем болуының ықтималдығын бағалаңыз.

189. Урнада 100 ақ 100 қара шарлар бар. Урнадан кез-келген шар алынып түсi анықталғаннан кейiн қайтарылады. Урнадан 50 рет шар алынды. Осы алынған шарлардың iшiнде ақ шарлардың саны мына интервалда (15, 35) болуының ықтималдығын бағалаңыз.

190.Кездейсоқ шама үлестiрiм заңымен берiлген

Х	1	2	3
Р	0,1	0,5	0,4

1. 
   |X-M(x)|<3 теңсiздiгiнiң орындалу ықтималдығын табыңыз.
   

2. 
   |X-M(x)|<3 теңсiздiгiнiң орындалу ықтималдығын бағалаңыз.
   

2. Чебышев теоремасы. Егер Х₁, Х₂, ..., Х_n қос-қостан тәуелсiз кездейсоқ шамаларының ақырлы математикалық үмiттерi бар болып және дисперсиялары тұрақты С санымен шектелген болса, онда кез-келген ε 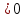саны үшiн

(2.5.3)

орындалады.

Бұл теореманы Чебышев теңсiздiгiн пайдаланып дәлелдегенде төмендегi бағалау алынады:
(2.5.4)

Егер М(х_i)=а болса, онда (2.5.3) формула былай жазылады:

(2.5.5)

Чебышев теоремасының мағынасын түсiндiру үшiн мысал қарастырайық. Айталық белгiлi бiр бұйымның бiр өлшемi а болсын. Соны өлшеу керек. Өлшеу кезiнде әртүрлi себептерге байланысты қате кетедi. Сондықтан өлшеу кезiнде алынған нәтиже кездейсоқ шама болады. Бұл Х кездейсоқ шамасының математикалық үмiтi өлшеп отырған а шамасына тең болады, ал дисперсиясы D(x) пайдаланып отырған прибордың дәлдiгiн көрсетедi. Тәуелсiз n өлшеу жасалық.

---

Сонда x₁, x₂, ..., x_n, сәйкес бiрiншi, екiншi, .... , n - шi өлшеулердiң нәтижелерi. Бұлардың өздерi кездейсоқ шамалар, олардың үлестiрiм заңдары Х-тiң үлестiрiм заңындай болады. Олай болса



кездейсоқ шамасыныңда үлестiрiм заңы да сондай болады. Бiрақта n өскен сайын бұл кездейсоқ шаманың кездейсоқтық сипаты бiрте-бiрте жоғала баcтайды да ол а-ға жақындай түседi.

Чебышев теоремасының практикалық маңызы мынада. Бiр нәрсенi өлшегенде мейлiнше дәл нәтиже алу үшiн оны бiрнеше рет өлшеп содан кейiн алған нәтижелердiң арифметикалық орташа мәнiн алу керек. Сондай-ақ, жоғарыдағы теңсіздіктерді пайдаланып жіберілген қате санынан аспау үшін қанша тәжірибе жүргізуге болатынын есептеуге болады.

4-мысал. Белгiлi бiр шаманың мәнi ретiнде мейлiнше көп өлшеулердiң арифметикалық орташа нәтижесi алынады. Әрбiр өлшеудiң мүмкiн мәндерiнiң орташа квадраттық ауытқуы 1 сантиметрден аспайды, деп қарастырып, 1000 өлшеуде алынған нәтиженiң берiлген шаманың шын мәнiнен ауытқуының абсолют шамасы 0,1 сантиметрден артық болмауының ықтималдығын бағалаңыз.

Шешуi: Әрбiр өлшеудiң нәтижесi кездейсоқ шама болады. Сондықтан 1000 өлшеудiң нәтижелерiн x₁, x₂, ..., x₁₀₀₀

тәуелсiз кездейсоқ шамалар жиынтығы ретiнде қарастырамыз. Сонда



1000 өлшеудiң арифметикалық орташа мәнi болады. Ол да кездейсоқ шама болады. Ендi өлшеп отырған шаманың шын мәнiн а деп қабылдасақ. Чебышев теоремасын пайдалануға болады:



Cөйтiп

5-мысал. Электрошамдар салынған 100 жәшiктiң әрқайсысынан олардың жану ұзақтығын анықтау үшiн бiр-бiрден электрошам алынды. Сөйтiп алынған шамдардың жану ұзақтығының арифметикалық орташа жану ұзақтығы есептелiндi. Осы арифметикалық орташа жану ұзақтығының жәшiктердегi барлық шамдардың жану ұзақтығының арифметикалық орташа жану ұзақтығынан айырмасының абсолют шамасының 2 сағаттан көп болмауының ықтималдығын бағалау керек. Шамдардың жану ұзақтығының орташа квадраттық ауытқуы 8 сағаттан аспайды.

Шешуi: Кездейсоқ шамаларға белгiлеу енгiзелiк. Х

---

_i i-iншi жәшiктен алынған электрошамның жану ұзақтығы, М(х_i) - әр жәшiктегi шамдардың арифметикалық орташа жану ұзақтығы. Сонда


алынған шамдардың арифметикалық орташа жану ұзақтығы, ал


100 жәшіктегі барлық шамдардың жану ұзақтығының арифметикалық орташа жану ұзақтығы. Сонымен есептiң шарты бойынша мына ықтималдықты бағалау керек.



Қарастырып отырған x₁, x₂, ..., x₁₀₀ кездейсоқ шамалар үшiн Чебышев теоремасының шарттары орындалады. Олай болса



Сөйтiп



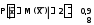
6-мысал. Белгiлi бiр шаманы өлшегенде алынған нәтижелер дисперсиясы 1-ден аспайтын кездейсоқ шама. Осы нәтижелердiң арифметикалық орташа мәнiнiң берiлген шаманың шын мәнiн ауытқуының абсолют шамасы 0,01-ден артпауының ықтималдығы 0,98 - ден кем болмауы үшiн қанша өлшеу керек?

Шешуi: Әрбiр өлшеу кезiнде алынған нәтижелер кездейсоқ шама және олар тәуелсiз. Белгiлеу енгiзелiк

x₁, x₂, ..., x_n

бiрiншi, екiншi, ... , n-шi өлшеулердiң нәтижелерi. Олай болса олардың арифметикалық орташа мәнi де



кездейсоқ шама. Ендi өлшеп отырған шаманың шын мәнiн а - деп белгiлесек, сонда бұл кездейсоқ шамалар Чебышев теоремасының шарттарын қанағаттандырады. Сондықтан

.

Oсыдан мына теңсiздiктi аламыз:



Соңғы теңсiздiктi шешiп болатынын көремiз.

7-мысал. Егер тәуелсiз x₁, x₂, ..., x_n кездейсоқ шамалар тiзбегi төмендегiдей үлестiрiм заңымен берiлсе

Xn	-3n	0	3n
P

---

онда осы кездейсоқ шамалар тiзбегiне Чебышев теоремасын қолдануға бола ма?

Шешуi: Берiлген кездейсоқ шамалар тiзбегiне Чебышев теоремасын пайдалану үшiн бұл тiзбектер екi шартты қанағаттандыру керек:

1)Олар қос-қостан тәуелсiз болу керек.

2)Олардың математикалық үмiттерi ақырлы болып, дисперсиялары тұрақты бiр С санымен шектелген болуы керек.

Берiлген кездейсоқ шамалар үшiн бiрiншi шарт орындалады, себебi есептiң шарты бойынша олар тәуелсiз кездейсоқ шамалар. Ал екiншi шарттың орындалуын тексеру қажет. Әуелi математикалық үмiттердi есептейiк:

M(x_n) = - + =0

Ендi х_n² үшiн үлестiрiм кестесiн жазайық.

Хn2	9n2	0	9n2
P

Осыдан М(х_n²) =

ақырында D(x)=

Cонымен М(х_n) ақырлы болады да, ал D(x_n) шектелген болады. Олай болса Чебышев теоремасын пайдалануға болады.

ЕСЕПТЕР
191. Әрбiр тәуелсiз 200 кездейсоқ шаманың дисперсиялары 4-тен аспайды. Осы кездейсоқ шамалардың арифметикалық орташасының олардың математикалық үмiттерiнiң арифметикалық орташасынан ауытқуының абсолют шамасы 0,3-тен артпауының ықтималдығын бағалау керек.

192. Жұмыс iстеуiнiң ұзақтығын ( 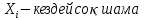) анықтау үшiн берiлген партиядан кез-келген 150 радиошам алынды. Радиошамның жұмыс iстеу ұзақтығының орташа квадраттық ауытқуы 6 сағаттан аспайды. Алынған 150 радиошамдардың жұмыс iстеуiнiң орташа ұзақтығының берiлген осы орташа мәннің математикалық үмітінен(берілген партиядағы шамдардың жұмыс істеу мерзімінің орташа ұзақтығы) айырымының абсолют шамасы 5 сағаттан кем болуының ықтималдығын бағалаңыз.

---

Смотрите также файлы

• Программа среднего профессионального образования 40. 02. 01 Право и организация социального обеспечения Дисциплина Физическая культура (2 семестр) Практическое задание 7.doc

• Родной язык Вопросы к промежуточной аттестации.docx

• Все чаще в современном обществе на различных уровнях затрагивается проблема ухудшения состояния здоровья нации.docx

• Влияние вредных привычек на организм человека.odt

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx