Файл: Ытималдытар теориясы жне математикалы статистика i тарау. Кездейсо оиалар негізгі тсініктер. Оиаларды трлері.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 784
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
193. Тәуелсiз кездейсоқ шамалар тiзбегi үлестiрiм қатарымен берiлген:
1.
| Хn | -5n | 0 | 5n |
| P |  |  | |
2.
| Хn | -2n | 2n |
| P | 0,5 | 0,5 |
Осы кездейсоқ шамалар тiзбектерiне Чебышев теоремасын пайдалануға бола ма?
194. Әрбiр 300 тәуелсiз кездейсоқ шамалардың дисперсиясы 5 - тен аспайды. Осы кездейсоқ шамалардың арифметикалық орташасының олардың математикалық үмiттерiнiң арифметикалық орташасынан ауытқуының абсолют шамасы 3 -тен аспауының ықтималдығын бағалаңыз.
195. Қос-қостан тәуелсiз кездейсоқ шамалардың дисперсиясы 10-нан аспайды. Осы кездейсоқ шамалардың арифметикалық орташасының олардың математикалық үмiттерiнiң арифметикалық орташасынан ауытқуының абсолют шамасы 0,25-тен аспауының ықтималдығы 0,99-дан кем болмауы ұшiн қанша кездейсоқ шама алыну керек?
196. Қос-қостан тәуелсiз кездейсоқ шамалардың әрқайсысының дисперсиясы 10-нан аспайды. Осындай 16000 кездейсоқ шамалардың арифметикалық орташасының олардың математикалық үмiттерiнiң арифметикалық орташасынан ауытқуының абсолют шамасы 0,25-тен артық болмауының ықтималдығын бағалаңыз.
197. Берiлген шаманың шын мәнi а. Осы шаманың мәнiн анықтау ұшiн өлшеулер жұргiзiледi. Осы өлшеулердiң арифметикалық орташа мәнiнiң а- дан ауытқуының абсолют шамасы 2-ден кем болуының ықтималдығы 0,95-ке тең болуы үшiн қанша өлшеу жасау керек? Әрбiр өлшеудiң орташа квадраттық ауытқуы 10-нан кiшi.
198. Таңдама әдiспен бидай дәндерiнiң орташа салмағын анықтау керек. Дәндердiң салмағының орташа квадраттық ауытқуы белгiлi ол - 0,04. таңдама әдiспен алынған дәндердiң орташа салмағының осы орташа салмақтың математикалық үмiтiнен (бұл берiлген партиядағы дәндердiң орташа салмағы) ауытқуының абсолют шамасы 0,01-ден артық болмауы 0,999 ықтималдықтан кем болмауы үшiн қанша дән тексерiлуi керек?
199. Тәуелсiз кездейсоқ шамалар тiзбегi үлестiрiм заңдарымен берiлген:
1.
| Хn | -5n | 0 | 5n |
| P |  |  | |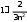
2.
| Хn | -n2 | 0 | n2 |
| P |  |  | |
Осы кездейсоқ шамалар тiзбегiне Чебышев теоремасын пайдалануға бола ма?
200. Тәуелсiз кездейсоқ шамалардың әрқайсысының дисперсиясы 4-тен аспайды. Осы кездейсоқ шамалардың арифметикалық орташа мәнiнiң олардың математикалық үмiттерiнiң арифметикалық орташа мәнiнен ауытқуының абсолют шамасы 0,5-тен аспауының ықтималдығы 0,99-дан кем бoлмауы үшiн қанша кездейсоқ шама болуы керек?
3. Бернулли теоремасы
Егер әрбiр тәуелсiз n сынақтарда (Бернулли схемасы бойынша)А оқиғасы тұрақты р ықтималдықпен m рет пайда болса, онда кез-келген
үшiн
(2.5.6)орындалады.
Бұл теореманы Чебышев теңсiздiгiн пайдаланып дәлелдегенде төмендегi бағалауды аламыз:
(2.5.7)8-мысал. Оқиға тәуелсiз сынақтарда тұрақты 0,2 ықтималдықпен пайда болады. Оқиғаның 900 сынақтарда пайда болуының салыстырмалы жиiлiгiнiң осы оқиғаның ықтималдығынан ауытқуының абсолют шамасы 0,04-ден кем болатындығының ықтималдығын бағалаңыз.
Шешуi: Есептiң шарттары Бернулли теоремасының шаттарымен сәйкес келедi. Сондықтан n=900, р=0,2, q=0,8, =0,04 екенiн ескерiп, iздеп отырған ықтималдықты бағалау ұшiн (2.5.7) формуланы пайдаланамыз.
Осыдан
9-мысал. А оқиғасының тәжiрибеде пайда болу ықтималдығы 0,75-ке тең. Осы тәжiрибелерде оқиғаның пайда болуының салыстырмалы жиiлiгiнiң оның ықтималдығынан ауытқуының абсолют шамасы 0,05-тен артық болмауының ықтималдығы 0,96-ға тең болу үшiн қанша тәжiрибе жасау керек?
Шешуi: Есептiң шарты бойынша
(2.5.7) формуладан
Осыдан n1875.
10-мысал. Зауыт дайындалған бұйымның 90 процентi бiрiншi сортқа жатады. Тексеруге 600 бұйым алынды. Тексеруге алынған бұйымдардың iшiндегi бiрiншi сортқа жататын бұйымдардың үлесiнiң оның ықтималдығынан ауытқуының абсолют шамасы
-нен кем болуының ықтималдығы 0,99-ға тең болуы үшiн бұл ауытқу қандай болуы керек?Шешуi: Есептiң шартын пайдалансақ онда мына теңдiктi жазамыз
Осыдан
,немесе =0,12.
ЕСЕПТЕР
201. Айталық зауыт шығарған сағаттың дәл жүру ықтималдығы 0,97-ге тең болсын. Алынған 1000 сағаттың iшiнде дәл жүретiн сағаттардың үлесi оның ықтималдығынан абсолют шамасы бойынша 0,02-ге ауытқуының ықтималдығын бағалаңыз.
202. Урнада 1000 ақ 2000 қара шарлар бар. Урнадан кез-келген шар алынып түсi анықталғаннан кейiн қайта урнаға салынады. Сөйтiп 300 сынақ жүргiзiледi. Осы сынақтарда ақ шардың m рет пайда болуы 80
203. Фабрикада шығарылған бұйымның сапасыз болуының ықтималдығы 0,015-ке тең. Фабрика шығарған бұйымдардың iшiндегi сапасыз бұйымдар үлесiнiң оның ықтималдығынан ауытқуының абсолют шамасы 0,005-тен аспауының ықтималдығы 0,807-ден кем болмауы үшiн қанша бұйым алу керек?
204. Даярланған радиошамдардың сапасын тексергенде олардың 95 процентi берiлген Т уақыттан кем жұмыс жасайды екен. Алынған 500 радиошамдардың iшiнде берiлген Т уақыттан кем жұмыс жасайтын радиошамдардың үлесiнiң оның ықтималдығынан айырмасының абсолют шамасы 0,02-ден артпауының ықтималдығын бағалаңыз.
205. Ойын кубын лақтырғанда 5 ұпай пайда болуының cалыстырмалы жиiлiгi мына интервалда [(
-0,05), ( +0,05)] жатуы 0,99 ықтималдықтан кем болмауы үшiн ойын кубын қанша рет лақтыру қажет?206. Әрбiр сынақтың жақсы нәтиже беру ықтималдығы 0,8-ге тең. 1000 тәуелсiз сынақтарда жақсы нәтиже беретiн сынақтардың салыстырмалы жиiлiгiнiң оның әрбiр сынақта пайда болу ықтималдығынан ауытқуының абсолют шамасы 0,05-тен кем болуының ықтималдығын бағалаңыз.
207. Ойын кубы 10000 рет лақтырылды. Осы сынақтарда 6 ұпай пайда болуының салыстырмалы жиiлiгiнiң оның ықтималдығынан ауытқуының абсолют шамасы 0,01-ден кем болуының ықтималдығын бағалаңыз.
208. Берiлген партиядағы жарамды деталдардың үлесi 98 процент екенi белгiлi болса, осы партияны тексергенде жарамды деталдардың пайда болуының салыстырмалы жиiлiгiнiң оның ықтималдығынан ауытқуының абсолют шамасы 0,02-ден кем болуының ықтималдығы 0,96-дан кем болмауы үшiн қанша деталь тексеру керек?
Сонымен үлкен сандар заңы - тәжiрибелердiң саны көбейген сайын алынған нәтижелердiң арифметикалық орташа нәтижесi тұрақты санға ұмтылатындығының шарттарын анықтайтын теоремалар жиыны болып табылады.
Сондай-ақ ықтималдықтар теориясында орталық шектiк теоремалардың да маңызы зор. Бұл теоремаларда қалыпты үлестiрім заңын қолдану шарттары қарастырылады. Егер қарастырып отырған кездейсоқ шама - өзара тәуелсiз мейлiнше көп кездейсоқ шамалардың қосындысы ретiнде жазуға болатын болса (ал әрбiр қосылғыштың қосындыға әсерi аз болса), онда берiлген кездейсоқ шама қалыпты үлестiрiммен берiледi деп қарастыруға болады. А.М.Ляпуновтың орталық шектiк теоремасының мәнi осында болып табылады.
МАТЕМАТИКАЛЫҚ СТАТИСТИКА ЭЛЕМЕНТТЕРI
III ТАРАУ. НЕГIЗГI ҰҒЫМДАР. ТАҢДАМАЛЫҚ ТӘСIЛ
Математикалық статистиканың негiзгi мақсаты сынақтар нәтижесiнде алынған статистикалық берiлгендердi талдап жалпылама кездейсоқ құбылыстарға тән статистикалық заңдылықтарды анықтау болып табылады.
Айталық күнделiктi тұрмыста бiртект
i объектiлердi сипаттайтын сандық және сапалық белгiлердi зерттеу керек болсын. Мысалы, бiртектi детальдер партиясын зерттеу қажет болса, онда сапалық белгi ретiнде детальдердiң стандарттылығы, ал сандық белгi ретiнде детальдiң бiр өлшемiн алуға болады.
Әрине, зерттеп отырған жинақтың әрбiр мүшесiн жекелеп алып қараса, онда зерттелiп отырған белгi (сандық немесе сапалық) бойынша толық мәлiмет алуға болады. Мұндай тексерудi жаппай бақылау деп атайды. Алайда қарастырып отырған жинақты белгiлi бiр белгi бойынша жаппай зерттеу көп жағдайда мүмкiн болмайды, кейде ол тиiмдi де емес.
Жинақтың элементтерi өте көп болса, онда жаппай бақылау жасау мүмкiн емес. Егерде, мысалы, электрошамдар партиясын стандарттылыққа зерттеу қажет болса, онда әрбiр шамның жану ұзақтығын тексеру керек болады. Барлық электрошамдарды бұлай тексеру мүмкiн емес, сондай-ақ, жанып кеткен электрошамның қажеттiгi жоқ.
Осындай жағдайларда берiлген жинақтан кiшкене көлемдi кездейсоқ бiр жинақ алынады. Содан кейiн осы кiшкене жинақты зерттейдi. Егер осындай кiшi көлемдi жинақты зерттеп үлкен (бас) жинақ туралы жеткiлiктi мәлiмет алуға болса, онда бас жинақты жаппай бақылаудың экономикалық тұрғыдан ешбiр қажеттiгi жоқ.
Берiлген жинақты осылай зерттеудi таңдамалық әдiс деп атайды.
Анықтама. Кездейсоқ шаманың барлық мүмкiн мәндерiнiң жиынын бас (генералдiк) жинақ деп атайды.
Анықтама. Бас жинақтан кездейсоқ алынған объектiлер жиынын таңдама жинақ немесе таңдама деп атайды.
Таңдама кездейсоқ шама Х-т