Файл: Ытималдытар теориясы жне математикалы статистика i тарау. Кездейсо оиалар негізгі тсініктер. Оиаларды трлері.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 783
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
iң тәуелсiз сынақтардың нәтижесiнде алынған мүмкiн мәндерi болып табылады, яғни 
Таңдамалар қандай талаптарды қанағаттандыруы керек? Басқаша айтқанда, бас жинақ туралы сенiмдi тұжырым жасау үшiн таңдама жинақ қандай болуы керек? Расында, кез келген таңдаманы зерттеп бас жинақ туралы нақты тұжырым жасау кейде мүмкiн емес болады. Мысалы, киiм фабрикасы шығарған бұйымын жәшiктерге жиғанда, төменгi жағына кiшiгiрiм кемшiлiгi бар бұйымдарды салып, ал үстiңгi жағына жоғары сапалы бұйымдарды текшелеп салсын делiк. Сонда егер таңдама жоғары қатардан алынса, онда сатуға әзiрленген барлық бұйым жоғары сапалы деп тұжырым жасалар едi. Бұл жағдайда ұсынылған тұжырым бас жинақ үшiн онша дұрыс еместiгi түсiнiктi. Сондықтан бас жинақтан алынған таңдама кездейсоқ алынуы керек. Осындай таңдама көрнектi (репрезентативтiк) таңдама деп аталады. Жоғары математика курсында таңдаманы алудың әртүрлi жолдары қарастырылады. Бiз төменде тек репрезентативтiк таңдамаларды қарастырамыз. Сөйтіп бас жинақты түгел зерттеудің орнына бас жинақтан алынған көлемі онша үлкен болмайтын таңдаманы зерттеп бас жинақ туралы белгілі бір тұжырымдар жасауға болады. Бас жинақты зерттеудің осындай әдісін таңдамалық әдіс деп атайды.Бұл әдіс бас жинақтың көлемі үлкен болған жағдайда қолданылады. Себебі көлемі үлкен жинақтың әрбір элементін түгел тексеріп шығу экономикалық тұрғыдан тиімсіз, ал кейбір жағдайда мүмкін емес.
Таңдаманың көлемi үлкен болған сайын оның негiзiнде жасалған тұжырым бас жинақ үшiн де орындалатындығына сенiм арта түседi.
Iс жүзiнде статистикалық талдау жасап отырған бас жинақтың үлестiрiмi, әдетте, белгiсiз болып келедi. Зерттеушiнiң қолында бас жинақтан алынған таңдама ғана болады. Сондықтан бас жинақ туралы тұжырымдарын осы таңдаманы талдап отырып алады.
Математикалық статистикада дискреттiк немесе үзiлiссiз сандық сипатты белгi Х-кездейсоқ шаманың мүмкiн мәндерiнен тұратын бас жинақ зерттелiнедi. Оның бас орташа, бас дисперсия т.с.с. сандық сипаттамаларын табу мәселесi практикалық қажеттiлiктен туындайды.
Айталық бас жинақтан варианталар деп аталынатын x1
,x2,...,xk элементтерiнен тұратын таңдама кездейсоқ терiлiп алынсын. Бұл таңдамада x1 вариантасы n1 рет, x2 вариантасы n2 рет, т.т., xк вариантасы nк рет қайталануы мүмкiн. Онда осы таңдаманы былай жазып
вариациялық қатар түрiнде жазылған таңдама деймiз.
Мұндағы ni - xi вариантасының жиiлiгi деп, ал n=
таңдаманың көлемi деп аталады.
Ендi осы таңдаманың сандық сипаттамалары арқылы бас жинақты зерттеуге болады. Осы таңдамалық тәсiл - математикалық статистиканың негiзгi тәсiлi болып табылады.
120>3>3>2>1>1>5>5>5>5>
§1. ТАҢДАМАНЫҢ САНДЫҚ СИПАТТАМАЛАРЫ
а) Эмпирикалық функция
(3.1.1)
Мұнда nx берілген х санынан кiшi болатын варианталардың жиiлiктерiнiң қосындысы. таңдаманың көлемi үлкен болғанда, осы функция арқылы бас жинақтың белгiсiз интегралдық үлестiрiм функциясы F(x) -ты жуықтап табуға болады.
б) Жиiлiктер полигоны.
Жазықтықтағы координаталары (x1,n1), (x2,n2),..., (xk,nk) нүктелерiн қосатын кесiндiлерден тұратын қисық сызық полигон деп аталады.
в) таңдамалық орташа
(3.1.2)
г) таңдамалық дисперсия
(3.1.3)
д) таңдамалық орташа квадраттық ауытқу.
(3.1.4) е) к-шы реттi бастапқы эмпирикалық момент
Мк=
, к=1,2,3,... (3.1.5)
ж) к -шы реттi орталық эмпирикалық момент
mк=
к=1,2,3,... (3.1.6)
з) таңдамалық асимметрия
(3.1.7)
и) таңдамалық эксцесс
(3.1.8)
Ескерту 1. Егер Хi варианталары үлкен сандар болса, жоғарыдағы (3.1.3) формулаларын тiкелей пайдаланбай, ui = xi - c деген шартты варианталарға көшiп, мына формулаларды пайдаланған ыңғайлы болады
(3.1.9)
(3.1.10)
Мұндағы С - "жалған нөл" деп аталынатын сан, оны өзiмiз жиiлiгi ең үлкен варианталарына шамалас етiп таңдаймыз.
1-мысал. Таңдама мына вариациялық қатар түрiнде берiлген:
Барлық сипаттамаларын табыңыз.
Шешуi: xi варианталары кiшкене сандар болғандықтан (3.1.1) - (3.1.8) формулаларын тiкелей қолданамыз.
а) таңдаманың көлемi n=10 және x 1 болса nx=0 (1-ден кiшi варианталар жоқ), демек F*(x)=0 , ал x<4 болса nx = 4, F*(x)=0,4, т.с.с. есептеулер жүргiзiп мына функцияны табамыз
.
Осы функцияның графигi төмендегiдей болғандықтан, эмпирикалық функцияны баспалдақ тәрiздес функция деп атау орынды.
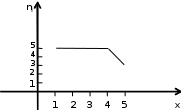
б) Жиiлiктер полигоны төмендегiдей сынық сызықболады.
в)
г)
д)
е)
ж)
, 
з)
и)
2-мысал. Берiлген вариациялық қатар арқылы хТ мен DT -ны табыңыз.
Шешуi: Варианталар үлкен сандар, сондықтан С=3900 деп алып, ui = хi-C шартты варианталарға көшейiк, яғни шартты вариациялық қатар аламыз.
Сонда (3.1.9), (3.1.10) формулаларын пайдалансақ
Ескерту 2. Егер сандық сипатты белгi Х үзiлiссiз таралған болса, оның бақыланған мәндерi кiретiн интервалды ұзындықтары h болатындай бiрнеше кiшi интервалдарға бөлiп, әрбiр бөлiкте жататын варианталардың жиiлiктерiнiң қосындысы ni анықталады. Сонда табаны (xi;xi+1) кiшi интервал, ал биiктiгi
болатын тiктөртбұрыштардан құралған фигураны - гистограмма деймiз.
3-мысал. Мына таңдаманың гистограммасын құрыңыз.
Шешуi: Абциссалар өсiнде ұзындықтары 4 болатын берiлген интервалдарды саламыз. Ендi табандары осы интервалдар болатын ал биiктiктерi болатын тiктөртбұрыштарды саламыз.
Гисторамманың ауданы n кв.өлшем бiрлiгiне тең болады, яғни таңдаманың көлеміне тең.
§2.ВАРИАНТАЛАРЫ БIРКЕЛКI ОРНАЛАСҚАН ТАҢДАМАЛАР. КӨБЕЙТIНДIЛЕР ТӘСIЛI
Таңдамадағы варианталар бiркелкi орналассын. Яғни қадам
h=x2-x1=x3-x2=...=xк-xк-1 тұрақты сан болсын. Бұл жағдайда "жалған нөл" - С ретiнде жиiлiгi ең үлкен болатын вариантаны алып, одан кейiн ui=(xi-c)/h шартты варианталарына көшiп, мынадай шартты моменттердi анықтаймыз.
k=1,2,... ,
сонда (3.2.1)
(3.2.2)
Таңдамалар қандай талаптарды қанағаттандыруы керек? Басқаша айтқанда, бас жинақ туралы сенiмдi тұжырым жасау үшiн таңдама жинақ қандай болуы керек? Расында, кез келген таңдаманы зерттеп бас жинақ туралы нақты тұжырым жасау кейде мүмкiн емес болады. Мысалы, киiм фабрикасы шығарған бұйымын жәшiктерге жиғанда, төменгi жағына кiшiгiрiм кемшiлiгi бар бұйымдарды салып, ал үстiңгi жағына жоғары сапалы бұйымдарды текшелеп салсын делiк. Сонда егер таңдама жоғары қатардан алынса, онда сатуға әзiрленген барлық бұйым жоғары сапалы деп тұжырым жасалар едi. Бұл жағдайда ұсынылған тұжырым бас жинақ үшiн онша дұрыс еместiгi түсiнiктi. Сондықтан бас жинақтан алынған таңдама кездейсоқ алынуы керек. Осындай таңдама көрнектi (репрезентативтiк) таңдама деп аталады. Жоғары математика курсында таңдаманы алудың әртүрлi жолдары қарастырылады. Бiз төменде тек репрезентативтiк таңдамаларды қарастырамыз. Сөйтіп бас жинақты түгел зерттеудің орнына бас жинақтан алынған көлемі онша үлкен болмайтын таңдаманы зерттеп бас жинақ туралы белгілі бір тұжырымдар жасауға болады. Бас жинақты зерттеудің осындай әдісін таңдамалық әдіс деп атайды.Бұл әдіс бас жинақтың көлемі үлкен болған жағдайда қолданылады. Себебі көлемі үлкен жинақтың әрбір элементін түгел тексеріп шығу экономикалық тұрғыдан тиімсіз, ал кейбір жағдайда мүмкін емес.
Таңдаманың көлемi үлкен болған сайын оның негiзiнде жасалған тұжырым бас жинақ үшiн де орындалатындығына сенiм арта түседi.
Iс жүзiнде статистикалық талдау жасап отырған бас жинақтың үлестiрiмi, әдетте, белгiсiз болып келедi. Зерттеушiнiң қолында бас жинақтан алынған таңдама ғана болады. Сондықтан бас жинақ туралы тұжырымдарын осы таңдаманы талдап отырып алады.
Математикалық статистикада дискреттiк немесе үзiлiссiз сандық сипатты белгi Х-кездейсоқ шаманың мүмкiн мәндерiнен тұратын бас жинақ зерттелiнедi. Оның бас орташа, бас дисперсия т.с.с. сандық сипаттамаларын табу мәселесi практикалық қажеттiлiктен туындайды.
Айталық бас жинақтан варианталар деп аталынатын x1
,x2,...,xk элементтерiнен тұратын таңдама кездейсоқ терiлiп алынсын. Бұл таңдамада x1 вариантасы n1 рет, x2 вариантасы n2 рет, т.т., xк вариантасы nк рет қайталануы мүмкiн. Онда осы таңдаманы былай жазып
| xi | x1 | x2 | x3 | ... | xk |
| ni | n1 | n2 | n3 | ... | nk |
вариациялық қатар түрiнде жазылған таңдама деймiз.
Мұндағы ni - xi вариантасының жиiлiгi деп, ал n=
таңдаманың көлемi деп аталады.Ендi осы таңдаманың сандық сипаттамалары арқылы бас жинақты зерттеуге болады. Осы таңдамалық тәсiл - математикалық статистиканың негiзгi тәсiлi болып табылады.
120>3>3>2>1>1>5>5>5>5>
§1. ТАҢДАМАНЫҢ САНДЫҚ СИПАТТАМАЛАРЫ
а) Эмпирикалық функция
(3.1.1)Мұнда nx берілген х санынан кiшi болатын варианталардың жиiлiктерiнiң қосындысы. таңдаманың көлемi үлкен болғанда, осы функция арқылы бас жинақтың белгiсiз интегралдық үлестiрiм функциясы F(x) -ты жуықтап табуға болады.
б) Жиiлiктер полигоны.
Жазықтықтағы координаталары (x1,n1), (x2,n2),..., (xk,nk) нүктелерiн қосатын кесiндiлерден тұратын қисық сызық полигон деп аталады.
в) таңдамалық орташа
(3.1.2)г) таңдамалық дисперсия
(3.1.3)д) таңдамалық орташа квадраттық ауытқу.
(3.1.4) е) к-шы реттi бастапқы эмпирикалық моментМк=
, к=1,2,3,... (3.1.5)ж) к -шы реттi орталық эмпирикалық момент
mк=
к=1,2,3,... (3.1.6)з) таңдамалық асимметрия
(3.1.7)и) таңдамалық эксцесс
(3.1.8)Ескерту 1. Егер Хi варианталары үлкен сандар болса, жоғарыдағы (3.1.3) формулаларын тiкелей пайдаланбай, ui = xi - c деген шартты варианталарға көшiп, мына формулаларды пайдаланған ыңғайлы болады
(3.1.9) (3.1.10)Мұндағы С - "жалған нөл" деп аталынатын сан, оны өзiмiз жиiлiгi ең үлкен варианталарына шамалас етiп таңдаймыз.
1-мысал. Таңдама мына вариациялық қатар түрiнде берiлген:
| xi | 1 | 4 | 5 |
| ni | 4 | 4 | 2 |
Барлық сипаттамаларын табыңыз.
Шешуi: xi варианталары кiшкене сандар болғандықтан (3.1.1) - (3.1.8) формулаларын тiкелей қолданамыз.
а) таңдаманың көлемi n=10 және x 1 болса nx=0 (1-ден кiшi варианталар жоқ), демек F*(x)=0 , ал x<4 болса nx = 4, F*(x)=0,4, т.с.с. есептеулер жүргiзiп мына функцияны табамыз
.
Осы функцияның графигi төмендегiдей болғандықтан, эмпирикалық функцияны баспалдақ тәрiздес функция деп атау орынды.
б) Жиiлiктер полигоны төмендегiдей сынық сызықболады.
в)
г)
д)
е)
ж)
, з)
и)
2-мысал. Берiлген вариациялық қатар арқылы хТ мен DT -ны табыңыз.
| xi | 3860 | 3900 | 3910 | 3913 |
| ni | 2 | 13 | 4 | 1 |
Шешуi: Варианталар үлкен сандар, сондықтан С=3900 деп алып, ui = хi-C шартты варианталарға көшейiк, яғни шартты вариациялық қатар аламыз.
| ui | -40 | 0 | 10 | 13 |
| ni | 2 | 13 | 4 | 1 |
Сонда (3.1.9), (3.1.10) формулаларын пайдалансақ
Ескерту 2. Егер сандық сипатты белгi Х үзiлiссiз таралған болса, оның бақыланған мәндерi кiретiн интервалды ұзындықтары h болатындай бiрнеше кiшi интервалдарға бөлiп, әрбiр бөлiкте жататын варианталардың жиiлiктерiнiң қосындысы ni анықталады. Сонда табаны (xi;xi+1) кiшi интервал, ал биiктiгi
болатын тiктөртбұрыштардан құралған фигураны - гистограмма деймiз.3-мысал. Мына таңдаманың гистограммасын құрыңыз.
| Интервал нөмiрi | Кiшi интервалдар | Варианталардың жиiлiктерiнiң қосындысы | Жиiлiктер тығыздығы |
| I | (xi ; xi+1) | ni | ni /h |
| 1 2 3 | (1 ; 5) (5; 9) (9; 13) | 20 30 50 | 5 7,5 12,5 |
Шешуi: Абциссалар өсiнде ұзындықтары 4 болатын берiлген интервалдарды саламыз. Ендi табандары осы интервалдар болатын ал биiктiктерi
болатын тiктөртбұрыштарды саламыз. Гисторамманың ауданы n кв.өлшем бiрлiгiне тең болады, яғни таңдаманың көлеміне тең.
§2.ВАРИАНТАЛАРЫ БIРКЕЛКI ОРНАЛАСҚАН ТАҢДАМАЛАР. КӨБЕЙТIНДIЛЕР ТӘСIЛI
Таңдамадағы варианталар бiркелкi орналассын. Яғни қадам
h=x2-x1=x3-x2=...=xк-xк-1 тұрақты сан болсын. Бұл жағдайда "жалған нөл" - С ретiнде жиiлiгi ең үлкен болатын вариантаны алып, одан кейiн ui=(xi-c)/h шартты варианталарына көшiп, мынадай шартты моменттердi анықтаймыз.
k=1,2,... ,сонда (3.2.1)
(3.2.2)