Файл: Ытималдытар теориясы жне математикалы статистика i тарау. Кездейсо оиалар негізгі тсініктер. Оиаларды трлері.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 782
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(3.2.3)
Осы тәсiлдi көбейтiндiлер тәсiлi деймiз.
4-мысал. Мына таңдаманың сандық сипаттамаларын табыңыз:
Шешуi: n=100; h=10; c=38 екенi түсiнiктi. Ендi мынадай есептеу кестесiн құрамыз.
яғни



Олай болса (3.2.2) - (3.2.3) бойынша



as = -0,89, ek=8,59.
Жоғарыда қарастырылған 1-4 мысалдарда таңдама вариациялық қатар арқылы берiлген. Көбiнесе таңдама жалпы түрде берiледi. Төменде таңдама жалпы түрде берiлген жағдайда интегралдық функция, сандық сипаттамалар қалай анықталатындығына мысал келтiрiлген.
5-мысал. Сандық сипатты белгiнiң бақыланған мәндерi төмендегi кестемен берiлген.
Шешуi.
1 кесте
Салыстырмалы жиiлiктер гистограммасын салу үшiн мына интервалдық қатарды қолданамыз.
2 кесте
Салыстырмалы жиiлiктер гистограммасын саламыз.
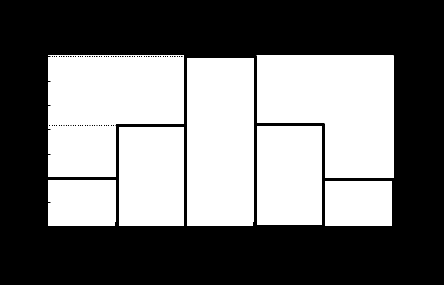
3 кесте
Ендi салыстырмалы жиiлiктер полигонын салу үшiн мына дискреттiк қатарды пайдаланамыз:
4 кесте
Полигонды тұрғызалық.
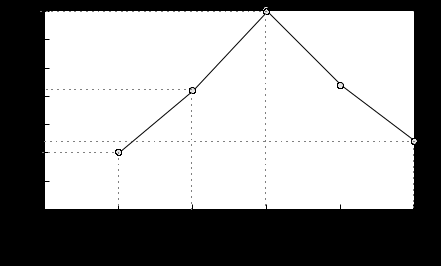
Сонда

Ендi -тiң графигiн (кумулятивтiк қисық) тұрғызамыз.
-тiң графигiн (кумулятивтiк қисық) тұрғызамыз.

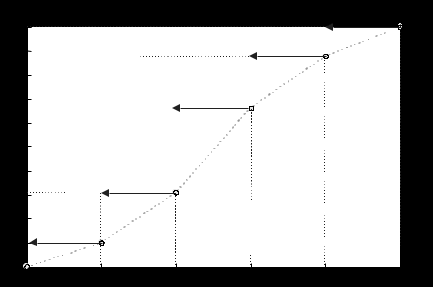
Бұл функцияның графигi
Осыдан
Сондай-ақ, , МD
, МD
ЕСЕПТЕР
209. 100 шағын дұкендерде сатылған тауарлардың айлық орташа көлемi ( млн.теңге) мына кестемен берiлген.
Осы тәсiлдi көбейтiндiлер тәсiлi деймiз.
4-мысал. Мына таңдаманың сандық сипаттамаларын табыңыз:
| .xi | 8 | 18 | 28 | 38 | 48 | 58 |
| ni | 5 | 2 | 3 | 71 | 9 | 10 |
Шешуi: n=100; h=10; c=38 екенi түсiнiктi. Ендi мынадай есептеу кестесiн құрамыз.
| Хi | ni | ui | ni ui | ni ui2 | ni ui3 | ni ui4 |
| 8 18 28 38 48 58 | 5 2 3 71 9 10 | -3 -2 -1 0 1 2 | -15 -4 -3 0 9 20 | 45 8 3 0 9 40 | -135 -16 -3 0 9 80 | 405 32 3 0 9 160 |
| | | | =7 | =105 | =-74 | =609 |
яғни
Олай болса (3.2.2) - (3.2.3) бойынша
as = -0,89, ek=8,59.
Жоғарыда қарастырылған 1-4 мысалдарда таңдама вариациялық қатар арқылы берiлген. Көбiнесе таңдама жалпы түрде берiледi. Төменде таңдама жалпы түрде берiлген жағдайда интегралдық функция, сандық сипаттамалар қалай анықталатындығына мысал келтiрiлген.
5-мысал. Сандық сипатты белгiнiң бақыланған мәндерi төмендегi кестемен берiлген.
| 01 | 00 | 25 | 18 | 04 | 14 | 25 | 14 | 16 | 08 |
| 09 | 11 | 16 | 04 | 11 | 12 | 14 | 21 | 20 | 12 |
| 09 | 12 | 18 | 25 | 22 | 21 | 20 | 11 | 01 | 22 |
| 03 | 04 | 18 | 22 | 09 | 14 | 12 | 02 | 08 | 19 |
| 01 | 15 | 11 | 24 | 12 | 10 | 09 | 16 | 09 | 14 |
| 24 | 12 | 16 | 16 | 09 | 06 | 07 | 08 | 12 | 16 |
| 16 | 16 | 19 | 14 | 11 | 07 | 21 | 20 | 11 | 12 |
| 09 | 20 | 13 | 14 | 13 | 14 | 09 | 13 | 16 | 17 |
| 12 | 11 | 19 | 06 | 06 | 14 | 21 | 18 | 12 | 16 |
| 06 | 11 | 02 | 08 | 06 | 14 | 14 | 13 | 15 | 09 |
-
Интервалдық вариациялық қатарды жаз. Салыстырмалы жиiлiктер гистограммасын сал.
-
Дискреттiк вариациялық қатарды жаз. Салыстырмалы жиiлiктер полигонын сал. -
Үзiлiссiз вариациялық қатардың эмпирикалық үлестiрiм функциясын тап. Графигiн сал. -
Дискреттiк вариациялық қатардың эмпирикалық үлестiрiм функциясын тап. Графигiн тұрғыз. -
Дискреттiк вариациялық қатардың сандық сипаттамаларын тап.
Шешуi.
-
Сандық сипатты белгiнiң бақыланған мәндерi [0;25] аралығында жатыр. Ендi h=5 деп алып осы аралықты кiшi интервалдарға бөлсек, сонда интервалдық вариациялық қатар мына түрде жазылады.
1 кесте
| интервалдар | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 |
| ni | 10 | 21 | 35 | 22 | 12 |
Салыстырмалы жиiлiктер гистограммасын салу үшiн мына интервалдық қатарды қолданамыз.
2 кесте
| интервалдар | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 |
| | 0,02 | 0,042 | 0,07 | 0,044 | 0,024 |
Салыстырмалы жиiлiктер гистограммасын саламыз.

-
Дискреттiк вариациялық қатарды жазу үшiн орынына кiшi интервалдардың ортасын аламыз.
орынына кiшi интервалдардың ортасын аламыз.
3 кесте
| хi | 2,5 | 7,5 | 12,5 | 17,5 | 22,5 |
| ni | 10 | 21 | 35 | 22 | 12 |
Ендi салыстырмалы жиiлiктер полигонын салу үшiн мына дискреттiк қатарды пайдаланамыз:
4 кесте
| хi | 2,5 | 7,5 | 12,5 | 17,5 | 22,5 |
| Wi | 0,1 | 0,21 | 0,35 | 0,22 | 0,12 |
Полигонды тұрғызалық.

-
Интервалдық вариациялық қатардың эмпирикалық үлестiрiм функциясының графигiн тұрғызу үшiн қосылған салыстырмалы жиiлiктер арқылы интервалдық вариациялық қатарды жазамыз.
| интервалдар | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 |
| қосылған салыстырмалы жиiлiк | 0,1 | 0,31 | 0,66 | 0,88 | 1 |
Сонда

Ендi

-
Ал дискреттiк вариациялық қатар үшiн эмпирикалық үлестiрiм функция

Бұл функцияның графигi

-
Дискреттiк вариациялық қатардың сандық сипаттамаларын 3 кестенi пайдаланып табамыз. Үшiншi кестеден дискреттiк қатардың варианталары бiркелкi орналасқандығы байқалады. Сондықтан сандық сипаттамаларды есептеу үшiн 3.2.1-3.2.3 формулаларын қолданамыз:
 ,
, 
| | | | | | | |
| 2.5 7.5 12.5 17.5 22.5 | 10 21 35 22 12 | -2 -1 0 1 2 | -20 -21 - 22 14 | 40 21 - 22 48 | -80 -21 - 22 96 | 160 21 - 22 192 |
| | 0.10 | 0 | 0.05 | 1.31 | 0.17 | 3.65 |
Осыдан

Сондай-ақ,
ЕСЕПТЕР
209. 100 шағын дұкендерде сатылған тауарлардың айлық орташа көлемi ( млн.теңге) мына кестемен берiлген.
| 33 | 34 | 33.5 | 36.5 | 34.5 | 35 | 34.5 | 34 | 34.5 | 35 |
| 35 | 35.5 | 35.5 | 35 | 35.5 | 35 | 35.5 | 37 | 35 | 35.5 |
| 35 | 35 | 35.5 | 35.5 | 35 | 35 | 35 | 35 | 35.5 | 36.5 |
| 35.5 | 35.5 | 35.5 | 35.5 | 35 | 38.5 | 37.5 | 37.5 | 34.5 | 34 |
| 34 | 34 | 33.5 | 37.5 | 38.5 | 36 | 36 | 36 | 36 | 36 |
| 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36.5 | 36.5 |
| 36.5 | 36.5 | 36.5 | 36.5 | 36.5 | 36.5 | 36.5 | 36.5 | 36.5 | 36 |
| 36 | 36 | 38 | 36 | 38 | 37 | 37 | 37 | 37.5 | 37.5 |
| 37.5 | 37.5 | 37.5 | 37.5 | 37.5 | 37.5 | 37. | 37 | 37.5 | 37 |
| 37 | 37.5 | 38.5 | 37.5 | 37 | 37.5 | 37.5 | 38 | 38.5 | 38.5 |