1. 
   Интервалдық вариациялық қатарды жазыңыз. Салыстырмалы жиiлiктер гистограммасын салыңыз.
   

2. 
   Дискреттiк вариациялық қатарды жазыңыз. Салыстырмалы жиiлiктер полигонын салыңыз.
   
3. 
   Үзiлiссiз вариациялық қатардың эмпирикалық функциясын жазыңыз. Графигiн салыңыз.
   
4. 
   Дискреттiк вариациялық қатардың эмпирикалық функциясын жазыңыз. Графигiн салыңыз.
   
5. 
   Дискреттiк вариациялық қатардың сандық сипаттамаларын табыңыз.
   

210. 
     .Мына таңдаманың сипаттамаларын және эмпирикалық функциясын табыңыз.
     

xi	-1	1	2	3
ni	3	4	2	1

211. 
     .Берiлген таңдаманың дисперсиясын табыңыз.
     

xi	2570	2590	2600	2640	2650
ni	2	3	10	4	1

212. 
     .Берiлген таңдаманы орташасы мен дисперсиясын табыңыз.
     

xi	18,6	19,0	19,4	19,8	20,2	20,6
ni	4	6	30	40	18	2

213. Мына таңдаманың асимметриясын табыңыз

xi	10	20	30	40	50	60	70
ni	5	15	50	16	4	5	5

214. Мына таңдаманың сипаттамаларын және эмпирикалық функциясын табыңыз

.

xi	12	14	16	18	20	22
ni	5	15	50	16	10	4

---

215. 
     .таңдаманың берiлген үлестірімі арқылы а) жиiлiктер гистограммасын салыңыз, б) дискреттiк вариациялық қатарды жазыңыз, в) эмпирикалық функциясын табыңыз
     

Интервал нөмiрi	Кiшi интервалдар	Жиiлiктер қосындысы	Жиiлiктер тығыздығы
I	(xi ; xi+1)	ni	ni /h
1 2 3 4 5	(2 ; 7) (7; 12) (12; 17) (17; 22) (22; 27)	5 10 25 6 4	1 2 5 6/5 4/5

216. 
     Таңдаманың орташасы мен дисперсиясын табыңыз
     

xi	18,4	18,9	19,3	19,6
ni	5	10	20	15

216. 
     Төменде доллардың Алматы қаласындағы 1999 ж. валюта алмастыру орындарындағы бағасы көрсетiлген
     

.

Доллар бағасы	87-87,1	87,1-87,2	87,2-87,3	87,3-87,4	87,4-87,5	87,5-87,6	87,6-87,7	87,7-87,8	87,8-88
алмастыру орындары-ның саны	5	8	12	20	25	15	8	4	3

таңдама орташасын және дисперсиясын табыңыз.

218. 
     60 шағын дұкенде айлық тауар сату көлемi (млн. теңге)мына кестемен берiлген.
     

50	57	55	62	51	63	64	60	61	72
56	55	63	64	61	71	73	74	71	64
57	61	58	63	59	62	64	69	51	63
64	66	67	68	57	58	59	60	52	56
65	67	69	67	66	63	61	69	53	58

---

1. 
   Интервалдық вариациялық қатарды жаз. Салыстырмалы жиiлiктер гистограммасын сал.
   

2. 
   Дискреттi вариациялық қатарды жаз. Салыстырмалы жиiлiктер полигонын сал.
   
3. 
   Үзiлiссiз вариациялық қатардың эмпирикалық функциясын тап. Графигiн сал.
   
4. 
   Дискреттiк вариациялық қатардың эмпирикалық функциясын тап. Графигiн сал.
   
5. 
   Дискреттiк вариациялық қатардың сандық сипаттамаларын тап.
   

IV ТАРАУ. БАС ЖИНАҚТЫҢ ПАРАМЕТРЛЕРIНІНІҢ СТАТИСТИКАЛЫҚ БАҒАЛАРЫ


Көп жағдайда бас жинақтың үлестірім заңы белгісіз болады. Үлестірім заңдары таңдаманы сапалы талдау нәтижесінде, таңдаманың гистограммасын немесе полигонын зерттеу нәтижесінде анықталады.

Айталық үлестірім заңының түрі анықталған болсын. Енді осы заңның параметрлерін анықтау қажет. Әрине, бұл параметрлердің тура мәнін анықтау мүмкін емес. Демек олардың мәндерін жуықтап анықтау керек , яғни бағалау керек. Белгісіз параметрлерді бағалау таңдаманың көмегімен жүргізіледі.

Бас жинақты сипаттаушы сандар оның параметрлері деп аталады. Осы параметрлерді статистикалық бағалаудың мәні мынада: көлемі шектелген таңдама көмегімен бас жинақтың белгісіз параметрлерін бағалау.

Айталық Ө бас жинақтың белгісіз параметрі болсын, ал Ө* оның таңдаманың көмегімен алынған бағалауы болсын. Әрбір таңдамалар үшiн өзгерiп отыратындықтан Ө* - кездейсоқ шама болады.

Статистикалық бағалаулар екі жолмен жүргізіледі:

1.Нүктелік бағалау – белгілі бір нүктені бағалау, яғни белгісіз параметрдің бір мәні бағаланады;

2.Интервалдық бағалау – берілген таңдаманың көмегімен белгісіз параметр Ө жататын интервалды берілген ықтималдықпен бағалау.

Статистистикалық бағалауларға үш шарт қойылады:

1. 
   . Егер М(Ө*)= Ө болса, онда Ө* ығыспаған баға деп аталады, ал басқа жағдайда ығысқан баға деп аталады.
   
2. 
   Егер болса, онда Ө* орнықты баға деп аталады, бұл жерде n - таңдама көлемi.
   
3. 
   Егер D(Ө*) = M(Ө*- Ө)² болса, онда Ө* тиімді баға деп аталады.
   

4>

---

§1. Бас жинақтың орташасы мен дисперсияларының нүктелік бағалары
Бас орташаның ығыспаған және орнықты нүктелiк бағасы таңдамалық орташа болады

Бас дисперсияның ығысқан бағасы таңдамалық дисперсия болады, ал жылжымаған бағасы түзетiлген таңдамалық дисперсия s² болады, мұнда n - таңдама көлемi.

1-мысал. Бас жинақтан мынадай таңдама алынған.

xi	4	5	7
ni	10	5	5

а) Бас орташаның ығыспаған бағасын табыңыз.

б) Бас дисперсияcының ығыспаған және ығысқан бағаларын табыңыз.

Шешуi:

а) таңдамалық орташа ығыспаған баға болады.



б) Ығысқан баға ретiнде D_T, ал ығыспаған баға ретiнде s² алынады

,
§2. НҮКТЕЛІК БАҒАЛАР. МОМЕНТТЕР ӘДIСI

Бұл әдiс бастапқы және орталық эмпирикалық моменттер өздерiне сәйкес бастапқы және орталық теориялық моменттердiң орнықты бағалары болатындығына негiзделген. Осы сәйкес моменттердi бiр-бiрiне теңестiре отырып, үлестiрiмнiң белгiсiз параметрiнiң нүктелiк бағалауларын табуға болады.

2-мысал. Көрсеткiштiк үлестiрiмнiң белгiсiз параметрi - ның нүктелiк бағасын табыңыз.

Шешуi: Бастапқы I-шi реттi эмпирикалық және теориялық моменттердi теңестiремiз.

₁=M₁

Көрсеткiштiк үлестiрiмнiң бiрiншi реттi бастапқы моментi

₁=M(x)= , ал M₁= болғандықтан =

---

теңдiгiн аламыз. Осыдан белгiсiз параметр -ның нұктелiк бағасы *= тең.

3-мысал. Берiлген таңдама бойынша моменттер әдiсiн қолданып қалыпты үлестiрiмнiң



белгiсiз a және  параметрлерiнiң нүктелiк бағасын табыңыз.

Шешуi: Бұл жағдайда екi а және  белгiсiз параметр болғандықтан бiрiншi, екiншi реттi теориялық және эмпирикалық моменттердi теңестiремiз.

₁=M₁, ₂=m₂.

Ары қарай ₁=M(x)=a, ₂=D(x)= ² және M₁= , m₂=D_T екенiн eскерсек, онда мынадай нүктелiк бағалар аламыз

a*= , *=

4-мысал. Берiлген таңдамасының сипаттамалары арқылы моменттер әдiсiмен бiрқалыпты үлестiрiмнiң

белгiсiз a және b параметрлерiнiң нүктелiк бағаларын табыңыз.

Шешуi: Бiрiншi және екiншi реттi эмпирикалық моменттердi теориялық моменттерге теңестiрейiк, яғни ₁=M₁, ₂=m₂.

Сонда ₁=M(x)= , ₂=D(x)= , M₁= , m₂=D_T екенiн ескере отырып мынадай теңдеулер системасын аламыз:


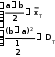
Осы системаны шеше отырып, a*= - , b*= +

---

Смотрите также файлы

• Программа среднего профессионального образования 40. 02. 01 Право и организация социального обеспечения Дисциплина Физическая культура (2 семестр) Практическое задание 7.doc

• Родной язык Вопросы к промежуточной аттестации.docx

• Все чаще в современном обществе на различных уровнях затрагивается проблема ухудшения состояния здоровья нации.docx

• Влияние вредных привычек на организм человека.odt

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx