Файл: Ытималдытар теориясы жне математикалы статистика i тарау. Кездейсо оиалар негізгі тсініктер. Оиаларды трлері.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 778
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
нұктелiк бағаларын табамыз.
§3. НЕҒҰРЛЫМ ШЫНДЫҚҚА ҰҚСАС ӘДIС
Берілген үлестірім заңының белгісіз параметрін неғұрлым шындыққа ұқсас әдісі бойынша нүктелік бағалау бір немесе бірнеше параметрлерден тәуелді функциялардың максимумын табуға негізделген.
1. Айталық Х - дискреттiк кездейсоқ шамасы болып, оның үлестірім заңының түрі белгілі болсын, яғни P(X= xi)=p(xi;ө) болсын, i=
; ө - белгiсiз параметр.
Анықтама. Х кездейсоқ шамасының шындыққа ұқсас функциясы деп
(4.3.1)
функциясын айтады.
Сонда Ө белгiсiз параметрiнiң нүктелiк бағасы ретiнде (4.3.1) функциясына максимум әперетiн Ө*=Ө*( х1, х2,..., хn) мәнiн аламыз, бұл баға неғұрлым шындыққа ұқсас баға деп аталады.
Ескерту: Есеп шығарған кезде lnL функциясын максимумге зерттеген ыңғайлы болады, себебi L және lnL функциялары Ө-нiң бiр мәнiнде максимумге жетедi.
1-мысал. Ең үлкен шындыққа ұқсас әдiспен биномды үлестiрiмнiң
Pn(k)=
рk(1-p)n-k
р- параметрiн бағалаңыз.
Шешуi: Шындыққа ұқсас L функциясын жазайық
.
L= Pn1(k1) Pn2(k2)=
(4.3.2)
Мұнда Ө=p және x1=k1, x2=k2 оқиғаның сәйкес n1 және n2 сынақтарда пайда болған саны.
Жоғарыда айтылған ескертуге сәйкес мына функцияны максимумге зерттеймiз.
LnL=ln(
)+(к1+к2)lnp+(n1+n2-к1-к2)ln(1-p) (4.3.3)
(4.3.3) функциясын бiр белгiсiз р-дан тәуелдi функция ретiнде қарастыра отырып, осы функцияның максимум нүктесiн табамыз.
Сонда р*=(к1+к2)/(n1+n2) мәнiн р параметрiнiң нүктелiк бағасы етiп алуға болатынына көзiмiз жетедi.
2. X - үзiлiссiз кездейсоқ шама болсын, ал f(x,Ө) белгiсiз параметр Ө-дан тәуелдi үлестiрiм тығыздығы дейiк.
Бұл жағдайда шындыққа ұқсас функцияны мына формуламен анықтаймыз
(4.3.4)
Ендi (4.3.4) функциясына максимум әперетiн Ө*=Ө*(x1,x2,...,xn) нүктесiн белгiсiз Ө параметрiнiң нүктелiк бағасы болады.
2-мысал. Көрсеткiштiк үлестiрiмнiң
f(x)= e-x (0
белгiсiз параметрiнiң нүктелiк бағасын табыңыз.
Шешуi: Шындыққа ұқсас функцияны құрамыз
(4.3.6)
Сонда
LnL=nln-(x1+x2+...+xn) (4.3.7)
Ендi осы (4.3.7) функциясын максимумге зерттесек =n/(x1+x2+...+xn)=
сын нүктесi максимум нүктесi болатынына көз жеткiземiз.
Яғни, белгiсiз параметрiнiң нүктелiк бағасы ретiнде
шамасын алуға болады.
3-мысал. Мына қалыпты үлестiрiмнiң
белгiсiз а және
параметрлерiнiң нүктелiк бағаларын табыңыз.
Шешуi: Шындыққа ұқсас функция құрамыз:
(4.3.8)
Мұндағы
- таңдамадағы варианталар. Ендi lnL функциясын табайық.
LnL=-nln-nln
-
(4.3.9)
(4.3.9) функциясын екi айнымалыдан тәуелдi функция ретiнде қарап, максимумге зерттеймiз
(4.3.10)
(4.3.10) жүйесін шешiп
нүктелiк бағаларын табамыз. Мұнда бiрiншi баға жылжымаған, ал екiншiсi жылжыған баға болады.
§4. ИНТЕРВАЛДЫҚ БАҒАЛАР
Бiр санмен ғана анықталатын нүктелiк баға, таңдаманың көлемi аз болғанда, өрескел қатеге соқтыруы мүмкiн, себебі бұл жағдайда нүктелік баға теориялық параметрге қаншалықты жақын жатқандығы туралы мәлімет бермейді. Сондықтан бас жинақтың белгiсiз параметрiнiң интервалдық бағасын, яғни осы параметрi жататындай (,) интервалын белгiлi бiр сенiмдiлiкпен табу мәселесiн қарастырылады.
Анықтама 1. параметрiнiң бағасы бойынша сенiмдiлiгi (сенiмдiлiк ықтималдығы) деп - теңсiздiгiнiң орындалу ықтималдығы - ны айтады, яғни Р(- )=, бұл жерде - бағаның дәлдiгi.
Анықтама 2. (-, +) - интервалын сенiмдiлiгiмен алынған сенiмдiлiк интервалы деп атайды.
1. Қалыпты үлестiрiммен берiлген сандық сипатты белгi Х шаманың белгiсiз а математикалық үмiтiн таңдамалық орташа
арқылы сенiмдiлiгiмен бағалау үшiн мынадай сенiмдiлiк интервалдарын аламыз:
а) Егер - бас орташа квадраттық ауытқу белгiлi болса, онда
(4.4.1)
t-саны Ф(t) =
-ға тең болатындай сан, оны Лаплас функциясының мәндер кестесiнен аламыз,
б) Егер - бас орташа квадраттық ауытқу белгiсiз болса, онда
(4.4.2)
Мұнда s - түзетiлген таңдамалық орташа квадраттық ауытқу,
- шамасы кестеден анықталады.
2. Қалыпты үлестiрiммен берiлген Х-тың белгісіз бас орташа квадраттық ауытқуы -ны берiлген сенiмдiлiгiмен бағалау үшін түзетiлген таңдамалық орташа квадраттық ауытқу s-ты пайдаланып мынадай сенiмдiлiк интервалдарын аламыз:
s(1-q)< 1 (4.4.4)
Бұл жерде q=q(n,) - кестеден алынады.
1-мысал. Бас орташа квадраттық ауытқуы 5 болатын қалыпты үлестiрiммен берiлген бас жинақтан алынған көлемi n=25 таңдамадан
=17 табылды. Бас жинақтың белгiсiз математикалық үмiтiн =0,99 сенiмдiлiгiмен бағалайтын интервалын табыңыз.
Шешуi: (4.4.1) формуласын пайдаланамыз. Егер
, онда кестеден t=2,57, яғни
Ocыдан
сенiмдiлiк интервалы.
2-мысал. Әлдебiр физикалық шама бiр құралмен 10 рет өлшенедi. Өлшеулердiң кездейсоқ қателерiнiң түзетiлген орташа квадраттық ауытқуы 0,5 - ке тең. Өлшеу құралының дәлдiгiн =0,99 сенiмдiлiгiмен табыңыз.
Шешуi: Құралдың дәлдiгi өлшеуде жiберiлген кездейсоқ қателердiң бас орташа квадраттық ауытқуымен сипатталады, яғни бiзге -ны бағалайтын сенiмдiлiк интервалын табу керек.
=0,99, n=10 болса, кестеден q=1,08 олай болса, (4.4.4) формуласын пайдалана отырып 0<<1,04 дәлдiктi анықтайтын сенiмдiлiк интервалын табамыз.
Е С Е П Т Е Р
220.Берiлген таңдама арқылы бас дисперсияның ығысқан және ығыспаған бағаларын табыңыз.
221. Х кездейсоқ шамасы Пуассон үлестiрiммен берiлген
моменттер әдiсiмен белгiсiз параметр -ның нүктелiк бағасын табыңыз.
222.Mоменттер әдiсiмен геометриялық үлестiрiмнiң
параметрi р -ның нүктелiк бағасын табыңыз.
223. Моменттер әдiсiмен Гамма үлестiрiмнiң
белгiсiз параметрлерi мен - ны бағала”ыз.
224. Жоғарыдағы 221 есептi неғұрлым шындыққа ұқсас әдiспен шығарыңыз.
225. Қалыпты үлестiрiлген бас жинақтың орташа квадраттық ауытқуын , таңдамалық орташасын
, түзетiлген таңдамалық орташа квадраттық ауытқуын s, таңдама көлемiн n деп алып, белгiсiз математикалық үмiт а - ны бағалайтын сенiмдiлiк интервалдарын табыңыз.
а) = 4,
10,2 , n=16, =0,99
б) = 5, 16,8 , n=25, =0,95
в) s = 3, 12 , n=9, =0,99
г) s = 7,2, 10 , n=40, =0,95
226. Детальдiң диаметрi арнаулы сызғышпен 6 рет өлшендi.
Өлшеулердiң кездейсоқ қателерiнiң түзетілген s орташа квадраттық ауытқуы- 0,4-ке тең. Сызғыштың дәлдiгiн =0,99 сенiмдiлiгiмен табыңыз.
227. Көлемi n болатындай таңдама арқылы түзетiлген таңдамалық орташа квадраттық ауытқу s анықталған. Қалыпты үлестiрiлген бас жинақтың бас орташа квадраттық ауытқуын бағалайтын сенiмдiлiк интервалын сенiмдiлiгiмен табыңыз.
а) n=5, =0,95 , s = 4,1
б) n=15, =0,99 , s = 3.
228. Таңдаманың сандық сипаттамалары (Ш-тарау, 2 мысал)
=12,75, 
=5,72 белгiлi. Бас жинақ қалыпты үлестiрiммен берiлген деп есептеп оның белгiсiз математикалық үмiтiн 
сенiмдiлiк ықтималдығымен бағалайтын сенiмдiлiк интервалын табыңыз.
229. Гипергеометриялық үлестiрiмнiң белгiсiз параметрiнiң моменттер әдiсiн
қолданып нүктелiк бағасын табыңыз.
230. Кездейсоқ шама биномдық үлестiрiммен берiлгендiгi анықталған.
а) Әрқайсысында 7 сынақтан (m=7) 15 тәжiрибе (n=15) жүргiзiлген:
б) Әрқайсысында 7 сынақтан 31 тәжiрибе жүргiзiлген
мұнда хi - оқиғаның әрбiр тәжiрибеде пайда болу саны, ni – тәжiрибелер саны. Моменттер әдiсiн қолданып белгiсiз р параметрiнiң нұктелiк бағасын табыңыз.
231. Кездейсоқ шама Пуассон үлестiрiмiмен берiлген. Төменде кездейсоқ оқиғаның пайда болу санының эмпирикалық үлестiрiмi келтiрiлген:
Моменттер әдiсiн қолданып Пуассон үлестiрiмiнiң белгiсiз
- параметрiнiң
нүктелiк бағасын табыңыз.
232. Кездейсоқ шама Х (атылған оқтың нысанадан ауытқуы) бiрқалыпты үлестiрiммен берiлген. хi – орташа ауытқуы деп алып, моменттер әдiсiн қолданып бiрқалыпты үлестiрiмнiң белгiсiз параметрлерiнiң (а және в) нүктелiк бағаларын табыңыз: а)
б)
233. Кездейсоқ шама көрсеткiштiк үлесiрiммен берiлген (белгiлi бiр механизмнiң жұмыс iстеу уақыты). Орташа жұмыс iстеу уақытын хi деп алып мына эмпирикалық үлестiрiмдер бойынша моменттер әдiсiн қолданып көрсеткiштiк үлестiрiмнiң белгiсiз параметрi -ны бағалаңыз:
б)
234. Кездейсоқ шама – дайындалған детальдiң стандарттан ауытқуы қалыпты
үлестiрiммен берiлген. хi (мм) – стандарттан ауытқуы деп алып, моменттер
әдiсiн қолданып қалыпты үлестiрiмнiң белгiсiз а және
параметрлерiнiң
нүктелiк бағаларын табыңыз:
а)
б)
V-ТАРАУ. СТАТИСТИКАЛЫҚ БОЛЖАМДАРДЫ ТЕКСЕРУ
1>
§1. НЕГIЗГI ҰҒЫМДАР. БОЛЖАМДЫ ТЕКСЕРУДIҢ
ЖАЛПЫ СХЕМАСЫ
Тәжірибеде әртүрлі сынақтардың нәтижесінде жаппай құбылыстардың сипаттамалары туралы ұсынылған болжамдарды тексеруге тура келеді.
Анықтама 1. Статистикалық болжам деп кездейсоқ шаманың үлестiрiмiнiң түрi немесе үлестiрiм параметрлерi туралы алдын-ала жасалатын болжамды айтады. Статистикалық болжам таңдаманың көмегiмен тексерiледi.
Алдымен нөлдiк болжам деп аталатын, тексерiлуге тиiс Но болжамы қарастырылады. Бұл болжамға қарсы болжамды альтернативтi деп атап, Н1 әрiпiмен белгiлеймiз. Мысалы: үлестiрiмнiң белгiсiз параметрi туралы нөлдiк болжам былай болса Но: = о , онда Н1 : о (Н1: >< o).
Статистикалық болжамдарды тексеру үшін статистикалық критерийлер қолданылады. Статистикалық критерий деп таңдаманың көмегімен нөлдік болжамды қабылдау немесе жоққа шығару ережесін айтады.
Cтатистикалық болжамды тексеру барысында екi түрлi қате жiберуiмiз мүмкiн.
Бiрiншi тектi қате - Но болжамы жоққа шығарылып Н1 болжамы қабылданады, бiрақ негiзiнде Но дұрыс.
Екiншi тектi қате - Но болжамын қабылдаймыз, бiрақ негiзiнде Н1 болжамы дұрыс.
Анықтама 2. Бiрiншi тектi қате жiберу ықтималдығын маңыздылық деңгейi деймiз де, әрiпiмен белгiлеймiз.
Болжамды тексерудiң жалпы схемасы:
1.Үлестiрiмi белгiлi статистикалық критерий деп аталатын F кездейсоқ шамасы енгiзiледi. Бұл шаманың әртүрлi еркiндiк дәрежелерi болып, ал үлестiрiмi қалыпты, Хи - квадрат, Стьюдент, Фишер-Снедекор үлестiрiмдерiмен берiлуi мүмкiн.
2.Таңдамалық (эмпирикалық) белгiлi деректерге сүйене отырып, критерийдiң бақыланатын мәнi Fбақ, анықталады.
3.Берiлген маңыздылық деңгейiнде F үлестiрiмiнiң сын нұктелерi кестесi арқылы, критерийдiң сындық мәнi - Fсын анықталады.
4. Егер Fбақсын болса, онда Но болжамын жоққа шығаруға негiз жоқ, ал егер Fбақ>Fсын болса, онда Но болжамы қабылданбайды.
§2. ПИРСОННЫҢ КЕЛIСIМДIК ХИ-КВАДРАТ
КРИТЕРИЙI
Математикалық статистиканың негізгі міндеттеріне сынақ нәтижелеріне сүйене отырып бас жинақ туралы ұсынылған үлестірім заңы туралы болжамды тексеру жатады. Алайда, біз үлестірім заңын және оның параметрлерін қаншалықты таңдап алғанмен қарастырып отырған таңдама жататындай шын үлестірім заңын таңдай алдық па жоқпа деген сұрақ туады. Сондықтан ұсынылған болжам берілген таңдамамен белгігілі бір маңыздылық деңгейінде үйлеседі деп айтады. Осыған байланысты ұсынылған үлестірім заңын тексеретін критерийлерді келісімділік критерийі деп атайды.
Егер үлестiрiм заңы белгiсiз болса, онда "бас жинақ А заңы бойынша үлестiрiлген", - деген нөлдiк болжам келiсiмдiк критерийлерi арқылы тексерiледi. Олардың бiрнеше түрi бар: Пирсон критерийi, Колмогоров критерийi, Смирнов критерийi т.т. Айталық
бас жинақтан алынған таңдама болсын. F(х)-ұсынылған үлестірім функциясы болсын. Берілген таңдама бойынша интервалдық қатар құрылады. Әрбір интервал үшін осы интервалдан мән қабылдау ықтималдығы(ұсынылған үлестірім заңы бойынша) және теориялық жиіліктер есептелінеді
.
Сөйтіп мына кесте алынады
Пирсонның келісімділік критерийін қарастыралық. Бұл критерий бойынша бас жинақтың параметрлеріне ешбір талап қойылмайды.
Но: "бас жинақ қалыпты үлестiрiммен берiлген" деген болжамды тексеру үшiн Пирсонның келiсiмдiк
критерийi қолданылады.
Егер h қадамымен бiркелкi орналасқан таңдама берiлсе,
онда Пирсон критерийі бойынша теориялық жиіліктер төмендегідей есептелінеді:
Теориялық және эмпирикалық жиiлiктердiң бiр-бiрiнен ауытқуы кездейсоқ па, бақылаулар саны аз ба, әлде "бас жинақ қалыпты үлестiрiммен берiлген" деген нөлдiк болжам дұрыс емес пе? Осы сұрақтарға Пирсон критерийi жауап бередi.
Тексеру схемасы:
1.Статистикалық критерий ретiнде мына кездейсоқ шаманы аламыз
(5.2.1)
Бұл шама - еркiндiк дәрежесi к=s-1-r болатын, Хи - квадрат үлестiрiмiмен берілген кездейсоқ шама. Мұнда s - таңдамадағы топтар саны, r - үлестiрiм параметрлерiнiң саны.
(5.2.2)
3. Берiлген маңыздылық деңгейiнде, Хи - квадрат үлестiрiмнiң сын нұктелерi кестесi арқылы
критерийдiң сындық мәнiн анықтаймыз.
4. Егер < 
- нөлдiк болжамды жоққа шығаруға негiз жоқ, ал егер > - нөлдiк болжам қабылданбайды. Екі жағдай болуы мүмкін:
- эмпирикалық және теориялық жиіліктер алдын ала берілген;
-эмпирикалық жиіліктер белгілі, онда теориялық жиіліктерді есептеу керек.
Осы екі жағдайға мысалдар қарастыралық
1-мысал. Эмпирикалық және теориялық жиiлiктер берiлген
Берiлген =0,05 маңыздылық деңгейiнде бас жинақтың қалыпты үлестiрiлгендiгi туралы болжамды тексерiңiз.
Шешуi: Критерийдiң бақыланатын мәнiн анықтау үшiн төмендегi кестенi құрамыз.
Сонымен
=3,66, ал критерийдiң еркiндiк дәрежесi к=s-1-r=5, мұнда берілген таңдамадағы мәліметтердің топтар саны s = 8, ал қарастырып отырған үлестірімнің параметрлерінің саны r = 2 (қалыпты үлестiрiм екi параметр арқылы анықталады). Онда кестеден 
(0,05; 5)=11,1. Сонымен <
- нөлдiк гипотезаны жоққа шығаруға негiз жоқ.
Алдыңғы 1-мысалда теориялық және эмпирикалық жиiлiктер берiлген болатын. Ендi тек эмпирикалық жиiлiктер белгiлi болғанда теориялық жиiлiктердi қалай есептеуге болатындығын көрсетелiк.
2-мысал. Интервалдық вариациялық қатар (III-тарау,1-кесте) мына түрде берiлген:
Пирсон критерийiн қолданып маңыздылық деңгейi
болғанда сандық белгiнiң бақыланған мәндерiн пайдаланып “бас жинақ қалыпты үлестiрiммен берiлген” -деген нөлдiк болжамды тексерiңiз.
Шешуі. 1.Бас жинақтың үлестiрiм заңы туралы болжам жасау үшiн, бiрiншiден, полигон және гистограмманың түрiне қараймыз. Мысалы, бас жинақ қалыпты үлестiрiммен берiлген деп болжам жасау үшiн:
а) Гистограмманың түрi Гаусс қисығының түрiне ұқсас болуы керек
б)Қалыпты үлестіріммен берілгендігін эмпирикалық ассиметрия мен эксцесстің көмегімен де анықтауға болады. Ол үшін эмпирикалық ассиметрия мен эксцесс мына теңсiздiктердi
және 
қанағаттандыруы керек.
Мұндағы таңдамалық асимметрия мен эксцестердің орташа квадраттық ауытқулары мына формулалар арқылы табылады
Қарастырып отырған мысал үшiн ек =0,8733,
, ал 
, 
олай болса және .
Ендi гистограммаға қарасақ (III тарау, §1), оның түрi Гаусс қисығына ұқсас. Демек, бас жинақ қалыпты үлестiрiммен берiлген деп болжам жасауға негiз бар.
, 
формулаларын қолданып теориялық жиiлiктердi есептеймiз.
Белгiлеу енгiзелiк
,
Есептеу кестесiн құрамыз
Сонда
бақ=1,7.
Ендi
маңыздылық деңгейiнде 
еркiндiк дәрежесi бойынша сын(0,05;2) кiтап соңындағы кестеден анықтаймыз:
сын(0,05;2)=6. Осыдан бақ< сын екенiн көремiз. Демек, бас жинақтың қалыпты үлестiрiммен берiлгендiгi туралы нөлдiк болжамды қабылдамауға негiз жоқ.
§3. ҚАЛЫПТЫ ҮЛЕСТIРIЛГЕН БАС ЖИНАҚТЫҢ БАС
ДИСПЕРСИЯЛАРЫН САЛЫСТЫРУ
Х және У қалыпты үлестiрiлген бас жинақтардан көлемдерi n1 және n2 - ге тең болатын таңдамалар алынып, олардың түзетiлген таңдамалық дисперсиялары
және 
табылсын. Берiлген маңыздылық деңгейiнде мына нөлдiк болжамды тексерейiк,
Ho : D(x)=D(y) (5.3.1)
H1 : D(x)>D(y) (5.3.2)
Статистикалық критерий ретiнде түзетiлген таңдамалық дисперсиялардың үлкенiнiң кiшiсiне қатынасын аламыз
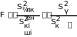(5.3.3)
Бұл шама еркiндiк дәрежелерi к1=m1-1, к2=m2-1 болатын, Фишер-Снедекор үлестiрiмiмен берiлген кездейсоқ шама. Бұл жерде
-қа сәйкес таңдаманың көлемi m1, ал 
- қа сәйкес таңдаманың көлемi m2.
Ендi берiлген деректер бойынша (5.3.3) арқылы Fбак анықтаймыз, одан кейiн Фишер-Снедекор үлестiрiмiнiң сын нүктелерi кестесiнен Fcын(,к1,к2) - ны табамыз, сонда егер Fбак < Fсын болса, онда нөлдiк болжамды қабылдамауға негiз жоқ, ал Fбак > Fсын болса нөлдiк болжам қабылданбайды.
Ескерту: Егер қарсылас болжам (5.3.2) түрiнде берiлмей, мына түрде берiлсе (H1:D(x)D(y)), онда критерийдiң сындық мәнi мына Fcын(
;к1;к2) санына тең болады.
1-мысал. Бiрдей детальдар жасайтын екi автоматты
станоктардың дәлдiктерiн салыстыру мақсатымен, бiрiншi станокта өнделген детальдардың 10-ы, ал екiншiсiнде өнделгендердiң 8-i өлшенiп мынадай деректер алынды
§3. НЕҒҰРЛЫМ ШЫНДЫҚҚА ҰҚСАС ӘДIС
Берілген үлестірім заңының белгісіз параметрін неғұрлым шындыққа ұқсас әдісі бойынша нүктелік бағалау бір немесе бірнеше параметрлерден тәуелді функциялардың максимумын табуға негізделген.
1. Айталық Х - дискреттiк кездейсоқ шамасы болып, оның үлестірім заңының түрі белгілі болсын, яғни P(X= xi)=p(xi;ө) болсын, i=
; ө - белгiсiз параметр.Анықтама. Х кездейсоқ шамасының шындыққа ұқсас функциясы деп
(4.3.1)функциясын айтады.
Сонда Ө белгiсiз параметрiнiң нүктелiк бағасы ретiнде (4.3.1) функциясына максимум әперетiн Ө*=Ө*( х1, х2,..., хn) мәнiн аламыз, бұл баға неғұрлым шындыққа ұқсас баға деп аталады.
Ескерту: Есеп шығарған кезде lnL функциясын максимумге зерттеген ыңғайлы болады, себебi L және lnL функциялары Ө-нiң бiр мәнiнде максимумге жетедi.
1-мысал. Ең үлкен шындыққа ұқсас әдiспен биномды үлестiрiмнiң
Pn(k)=
рk(1-p)n-kр- параметрiн бағалаңыз.
Шешуi: Шындыққа ұқсас L функциясын жазайық
.
L= Pn1(k1) Pn2(k2)=
(4.3.2)Мұнда Ө=p және x1=k1, x2=k2 оқиғаның сәйкес n1 және n2 сынақтарда пайда болған саны.
Жоғарыда айтылған ескертуге сәйкес мына функцияны максимумге зерттеймiз.
LnL=ln(
)+(к1+к2)lnp+(n1+n2-к1-к2)ln(1-p) (4.3.3)(4.3.3) функциясын бiр белгiсiз р-дан тәуелдi функция ретiнде қарастыра отырып, осы функцияның максимум нүктесiн табамыз.
Сонда р*=(к1+к2)/(n1+n2) мәнiн р параметрiнiң нүктелiк бағасы етiп алуға болатынына көзiмiз жетедi.
2. X - үзiлiссiз кездейсоқ шама болсын, ал f(x,Ө) белгiсiз параметр Ө-дан тәуелдi үлестiрiм тығыздығы дейiк.
Бұл жағдайда шындыққа ұқсас функцияны мына формуламен анықтаймыз
(4.3.4)Ендi (4.3.4) функциясына максимум әперетiн Ө*=Ө*(x1,x2,...,xn) нүктесiн белгiсiз Ө параметрiнiң нүктелiк бағасы болады.
2-мысал. Көрсеткiштiк үлестiрiмнiң
f(x)= e-x (0
белгiсiз параметрiнiң нүктелiк бағасын табыңыз.
Шешуi: Шындыққа ұқсас функцияны құрамыз
(4.3.6)Сонда
LnL=nln-(x1+x2+...+xn) (4.3.7)
Ендi осы (4.3.7) функциясын максимумге зерттесек =n/(x1+x2+...+xn)=
сын нүктесi максимум нүктесi болатынына көз жеткiземiз.
Яғни, белгiсiз параметрiнiң нүктелiк бағасы ретiнде
шамасын алуға болады.
3-мысал. Мына қалыпты үлестiрiмнiң
белгiсiз а және
параметрлерiнiң нүктелiк бағаларын табыңыз.Шешуi: Шындыққа ұқсас функция құрамыз:
(4.3.8)Мұндағы
- таңдамадағы варианталар. Ендi lnL функциясын табайық.LnL=-nln-nln
- (4.3.9)(4.3.9) функциясын екi айнымалыдан тәуелдi функция ретiнде қарап, максимумге зерттеймiз
(4.3.10) (4.3.10) жүйесін шешiп
нүктелiк бағаларын табамыз. Мұнда бiрiншi баға жылжымаған, ал екiншiсi жылжыған баға болады.
§4. ИНТЕРВАЛДЫҚ БАҒАЛАР
Бiр санмен ғана анықталатын нүктелiк баға, таңдаманың көлемi аз болғанда, өрескел қатеге соқтыруы мүмкiн, себебі бұл жағдайда нүктелік баға теориялық параметрге қаншалықты жақын жатқандығы туралы мәлімет бермейді. Сондықтан бас жинақтың белгiсiз параметрiнiң интервалдық бағасын, яғни осы параметрi жататындай (,) интервалын белгiлi бiр сенiмдiлiкпен табу мәселесiн қарастырылады.
Анықтама 1. параметрiнiң бағасы бойынша сенiмдiлiгi (сенiмдiлiк ықтималдығы) деп - теңсiздiгiнiң орындалу ықтималдығы - ны айтады, яғни Р(- )=, бұл жерде - бағаның дәлдiгi.
Анықтама 2. (-, +) - интервалын сенiмдiлiгiмен алынған сенiмдiлiк интервалы деп атайды.
1. Қалыпты үлестiрiммен берiлген сандық сипатты белгi Х шаманың белгiсiз а математикалық үмiтiн таңдамалық орташа
арқылы сенiмдiлiгiмен бағалау үшiн мынадай сенiмдiлiк интервалдарын аламыз:а) Егер - бас орташа квадраттық ауытқу белгiлi болса, онда
(4.4.1)t-саны Ф(t) =
-ға тең болатындай сан, оны Лаплас функциясының мәндер кестесiнен аламыз,б) Егер - бас орташа квадраттық ауытқу белгiсiз болса, онда
(4.4.2)Мұнда s - түзетiлген таңдамалық орташа квадраттық ауытқу,
- шамасы кестеден анықталады.2. Қалыпты үлестiрiммен берiлген Х-тың белгісіз бас орташа квадраттық ауытқуы -ны берiлген сенiмдiлiгiмен бағалау үшін түзетiлген таңдамалық орташа квадраттық ауытқу s-ты пайдаланып мынадай сенiмдiлiк интервалдарын аламыз:
s(1-q)<
Бұл жерде q=q(n,) - кестеден алынады.
1-мысал. Бас орташа квадраттық ауытқуы 5 болатын қалыпты үлестiрiммен берiлген бас жинақтан алынған көлемi n=25 таңдамадан
=17 табылды. Бас жинақтың белгiсiз математикалық үмiтiн =0,99 сенiмдiлiгiмен бағалайтын интервалын табыңыз.Шешуi: (4.4.1) формуласын пайдаланамыз. Егер
, онда кестеден t=2,57, яғни Ocыдан
сенiмдiлiк интервалы.2-мысал. Әлдебiр физикалық шама бiр құралмен 10 рет өлшенедi. Өлшеулердiң кездейсоқ қателерiнiң түзетiлген орташа квадраттық ауытқуы 0,5 - ке тең. Өлшеу құралының дәлдiгiн =0,99 сенiмдiлiгiмен табыңыз.
Шешуi: Құралдың дәлдiгi өлшеуде жiберiлген кездейсоқ қателердiң бас орташа квадраттық ауытқуымен сипатталады, яғни бiзге -ны бағалайтын сенiмдiлiк интервалын табу керек.
=0,99, n=10 болса, кестеден q=1,08 олай болса, (4.4.4) формуласын пайдалана отырып 0<<1,04 дәлдiктi анықтайтын сенiмдiлiк интервалын табамыз.
Е С Е П Т Е Р
-
Берiлген таңдама арқылы бас орташаның ығыспаған бағасын табыңыз.
| Хi | 3 | 6 | 9 | 12 |
| ni | 15 | 18 | 12 | 5 |
220.Берiлген таңдама арқылы бас дисперсияның ығысқан және ығыспаған бағаларын табыңыз.
| Хi | 5 | 12 | 13 | 15 | 20 |
| ni | 12 | 15 | 20 | 40 | 13 |
221. Х кездейсоқ шамасы Пуассон үлестiрiммен берiлген
моменттер әдiсiмен белгiсiз параметр -ның нүктелiк бағасын табыңыз.
222.Mоменттер әдiсiмен геометриялық үлестiрiмнiң
параметрi р -ның нүктелiк бағасын табыңыз.223. Моменттер әдiсiмен Гамма үлестiрiмнiң
белгiсiз параметрлерi мен - ны бағала”ыз.
224. Жоғарыдағы 221 есептi неғұрлым шындыққа ұқсас әдiспен шығарыңыз.
225. Қалыпты үлестiрiлген бас жинақтың орташа квадраттық ауытқуын , таңдамалық орташасын
, түзетiлген таңдамалық орташа квадраттық ауытқуын s, таңдама көлемiн n деп алып, белгiсiз математикалық үмiт а - ны бағалайтын сенiмдiлiк интервалдарын табыңыз.а) = 4,
10,2 , n=16, =0,99б) = 5,
16,8 , n=25, =0,95в) s = 3,
12 , n=9, =0,99г) s = 7,2,
10 , n=40, =0,95226. Детальдiң диаметрi арнаулы сызғышпен 6 рет өлшендi.
Өлшеулердiң кездейсоқ қателерiнiң түзетілген s орташа квадраттық ауытқуы- 0,4-ке тең. Сызғыштың дәлдiгiн =0,99 сенiмдiлiгiмен табыңыз.
227. Көлемi n болатындай таңдама арқылы түзетiлген таңдамалық орташа квадраттық ауытқу s анықталған. Қалыпты үлестiрiлген бас жинақтың бас орташа квадраттық ауытқуын бағалайтын сенiмдiлiк интервалын сенiмдiлiгiмен табыңыз.
а) n=5, =0,95 , s = 4,1
б) n=15, =0,99 , s = 3.
228. Таңдаманың сандық сипаттамалары (Ш-тарау, 2 мысал)
=12,75, =5,72 белгiлi. Бас жинақ қалыпты үлестiрiммен берiлген деп есептеп оның белгiсiз математикалық үмiтiн сенiмдiлiк ықтималдығымен бағалайтын сенiмдiлiк интервалын табыңыз.229. Гипергеометриялық үлестiрiмнiң белгiсiз параметрiнiң моменттер әдiсiн
қолданып нүктелiк бағасын табыңыз.
230. Кездейсоқ шама биномдық үлестiрiммен берiлгендiгi анықталған.
а) Әрқайсысында 7 сынақтан (m=7) 15 тәжiрибе (n=15) жүргiзiлген:
| xi | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| ni | 7 | 3 | 1 | 1 | 1 | 1 | 1 |
б) Әрқайсысында 7 сынақтан 31 тәжiрибе жүргiзiлген
| xi | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| ni | 13 | 7 | 2 | 2 | 2 | 2 | 2 |
мұнда хi - оқиғаның әрбiр тәжiрибеде пайда болу саны, ni – тәжiрибелер саны. Моменттер әдiсiн қолданып белгiсiз р параметрiнiң нұктелiк бағасын табыңыз.
231. Кездейсоқ шама Пуассон үлестiрiмiмен берiлген. Төменде кездейсоқ оқиғаның пайда болу санының эмпирикалық үлестiрiмi келтiрiлген:
| xi | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| ni | 300 | 200 | 100 | 80 | 70 | 30 | 20 |
Моменттер әдiсiн қолданып Пуассон үлестiрiмiнiң белгiсiз
- параметрiнiңнүктелiк бағасын табыңыз.
232. Кездейсоқ шама Х (атылған оқтың нысанадан ауытқуы) бiрқалыпты үлестiрiммен берiлген. хi – орташа ауытқуы деп алып, моменттер әдiсiн қолданып бiрқалыпты үлестiрiмнiң белгiсiз параметрлерiнiң (а және в) нүктелiк бағаларын табыңыз: а)
| xi | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
| ni | 17 | 13 | 19 | 16 | 20 | 21 | 14 | 18 | 22 |
| | | | | | | | | | |
б)
| xi | 3 | 6 | 9 | 12 | 15 | 18 | 21 |
| ni | 4 | 6 | 5 | 2 | 7 | 4 | 5 |
233. Кездейсоқ шама көрсеткiштiк үлесiрiммен берiлген (белгiлi бiр механизмнiң жұмыс iстеу уақыты). Орташа жұмыс iстеу уақытын хi деп алып мына эмпирикалық үлестiрiмдер бойынша моменттер әдiсiн қолданып көрсеткiштiк үлестiрiмнiң белгiсiз параметрi
-ны бағалаңыз:| xi | 1 | 6 | 11 | 16 | 21 | 26 |
| ni | 142 | 35 | 14 | 5 | 3 | 1 |
б)
| xi | 13 | 16 | 19 | 22 | 25 | 28 | 31 |
| ni | 89 | 30 | 20 | 10 | 8 | 2 | 1 |
234. Кездейсоқ шама – дайындалған детальдiң стандарттан ауытқуы қалыпты
үлестiрiммен берiлген. хi (мм) – стандарттан ауытқуы деп алып, моменттер
әдiсiн қолданып қалыпты үлестiрiмнiң белгiсiз а және
параметрлерiнiңнүктелiк бағаларын табыңыз:
а)
| xi | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| ni | 7 | 10 | 24 | 28 | 24 | 20 | 24 | 20 | 10 | 8 | 6 |
б)
| xi | 3 | 7 | 11 | 15 | 19 | 23 | 27 |
| ni | 2 | 4 | 7 | 17 | 6 | 3 | 1 |
V-ТАРАУ. СТАТИСТИКАЛЫҚ БОЛЖАМДАРДЫ ТЕКСЕРУ
1>
1 ... 6 7 8 9 10 11 12 13 ... 22
§1. НЕГIЗГI ҰҒЫМДАР. БОЛЖАМДЫ ТЕКСЕРУДIҢ
ЖАЛПЫ СХЕМАСЫ
Тәжірибеде әртүрлі сынақтардың нәтижесінде жаппай құбылыстардың сипаттамалары туралы ұсынылған болжамдарды тексеруге тура келеді.
Анықтама 1. Статистикалық болжам деп кездейсоқ шаманың үлестiрiмiнiң түрi немесе үлестiрiм параметрлерi туралы алдын-ала жасалатын болжамды айтады. Статистикалық болжам таңдаманың көмегiмен тексерiледi.
Алдымен нөлдiк болжам деп аталатын, тексерiлуге тиiс Но болжамы қарастырылады. Бұл болжамға қарсы болжамды альтернативтi деп атап, Н1 әрiпiмен белгiлеймiз. Мысалы: үлестiрiмнiң белгiсiз параметрi туралы нөлдiк болжам былай болса Но: = о , онда Н1 : о (Н1: >< o).
Статистикалық болжамдарды тексеру үшін статистикалық критерийлер қолданылады. Статистикалық критерий деп таңдаманың көмегімен нөлдік болжамды қабылдау немесе жоққа шығару ережесін айтады.
Cтатистикалық болжамды тексеру барысында екi түрлi қате жiберуiмiз мүмкiн.
Бiрiншi тектi қате - Но болжамы жоққа шығарылып Н1 болжамы қабылданады, бiрақ негiзiнде Но дұрыс.
Екiншi тектi қате - Но болжамын қабылдаймыз, бiрақ негiзiнде Н1 болжамы дұрыс.
Анықтама 2. Бiрiншi тектi қате жiберу ықтималдығын маңыздылық деңгейi деймiз де, әрiпiмен белгiлеймiз.
Болжамды тексерудiң жалпы схемасы:
1.Үлестiрiмi белгiлi статистикалық критерий деп аталатын F кездейсоқ шамасы енгiзiледi. Бұл шаманың әртүрлi еркiндiк дәрежелерi болып, ал үлестiрiмi қалыпты, Хи - квадрат, Стьюдент, Фишер-Снедекор үлестiрiмдерiмен берiлуi мүмкiн.
2.Таңдамалық (эмпирикалық) белгiлi деректерге сүйене отырып, критерийдiң бақыланатын мәнi Fбақ, анықталады.
3.Берiлген маңыздылық деңгейiнде F үлестiрiмiнiң сын нұктелерi кестесi арқылы, критерийдiң сындық мәнi - Fсын анықталады.
4. Егер Fбақ
§2. ПИРСОННЫҢ КЕЛIСIМДIК ХИ-КВАДРАТ
КРИТЕРИЙI
Математикалық статистиканың негізгі міндеттеріне сынақ нәтижелеріне сүйене отырып бас жинақ туралы ұсынылған үлестірім заңы туралы болжамды тексеру жатады. Алайда, біз үлестірім заңын және оның параметрлерін қаншалықты таңдап алғанмен қарастырып отырған таңдама жататындай шын үлестірім заңын таңдай алдық па жоқпа деген сұрақ туады. Сондықтан ұсынылған болжам берілген таңдамамен белгігілі бір маңыздылық деңгейінде үйлеседі деп айтады. Осыған байланысты ұсынылған үлестірім заңын тексеретін критерийлерді келісімділік критерийі деп атайды.
Егер үлестiрiм заңы белгiсiз болса, онда "бас жинақ А заңы бойынша үлестiрiлген", - деген нөлдiк болжам келiсiмдiк критерийлерi арқылы тексерiледi. Олардың бiрнеше түрi бар: Пирсон критерийi, Колмогоров критерийi, Смирнов критерийi т.т. Айталық
| х1 | х2 | х3 | ... | хm |
бас жинақтан алынған таңдама болсын. F(х)-ұсынылған үлестірім функциясы болсын. Берілген таңдама бойынша интервалдық қатар құрылады. Әрбір интервал үшін осы интервалдан мән қабылдау ықтималдығы(ұсынылған үлестірім заңы бойынша) және теориялық жиіліктер есептелінеді
. Сөйтіп мына кесте алынады
| Эмпирикалық жиiлiктер | 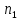 | n2 | n3 | ... | nm |
| Теориялық жиiлiктер |  |  |  | ... |  |
Пирсонның келісімділік критерийін қарастыралық. Бұл критерий бойынша бас жинақтың параметрлеріне ешбір талап қойылмайды.
Но: "бас жинақ қалыпты үлестiрiммен берiлген" деген болжамды тексеру үшiн Пирсонның келiсiмдiк
критерийi қолданылады.Егер h қадамымен бiркелкi орналасқан таңдама берiлсе,
| хi | х1 | х2 | х3 | ... | хm |
| ni | n1 | n2 | n3 | ... | nm |
онда Пирсон критерийі бойынша теориялық жиіліктер төмендегідей есептелінеді:
Теориялық және эмпирикалық жиiлiктердiң бiр-бiрiнен ауытқуы кездейсоқ па, бақылаулар саны аз ба, әлде "бас жинақ қалыпты үлестiрiммен берiлген" деген нөлдiк болжам дұрыс емес пе? Осы сұрақтарға Пирсон критерийi жауап бередi.
Тексеру схемасы:
1.Статистикалық критерий ретiнде мына кездейсоқ шаманы аламыз
(5.2.1)Бұл шама - еркiндiк дәрежесi к=s-1-r болатын, Хи - квадрат үлестiрiмiмен берілген кездейсоқ шама. Мұнда s - таңдамадағы топтар саны, r - үлестiрiм параметрлерiнiң саны.
-
Берiлген деректерге сүйене отырып, критерийдiң бақыланатын мәнiн анықтаймыз.
(5.2.2)3. Берiлген маңыздылық деңгейiнде, Хи - квадрат үлестiрiмнiң сын нұктелерi кестесi арқылы
критерийдiң сындық мәнiн анықтаймыз. 4. Егер
< - нөлдiк болжамды жоққа шығаруға негiз жоқ, ал егер > - нөлдiк болжам қабылданбайды. Екі жағдай болуы мүмкін:- эмпирикалық және теориялық жиіліктер алдын ала берілген;
-эмпирикалық жиіліктер белгілі, онда теориялық жиіліктерді есептеу керек.
Осы екі жағдайға мысалдар қарастыралық
1-мысал. Эмпирикалық және теориялық жиiлiктер берiлген
| Эмпирикалық жиiлiктер | 5 | 13 | 39 | 75 | 105 | 83 | 32 | 14 |
| Теориялық жиiлiктер | 3 | 15 | 41 | 80 | 101 | 77 | 38 | 13 |
Берiлген =0,05 маңыздылық деңгейiнде бас жинақтың қалыпты үлестiрiлгендiгi туралы болжамды тексерiңiз.
Шешуi: Критерийдiң бақыланатын мәнiн анықтау үшiн төмендегi кестенi құрамыз.
| I |  |  |  |  |  |
| 1 2 3 4 5 6 7 8 | 5 13 39 75 105 83 32 14 | 3 15 41 80 101 77 38 13 | 2 -2 -2 -2 4 6 -6 1 | 4 4 4 25 16 36 36 1 | 1,333 0,267 0,097 0,3125 0,158 0,468 0,947 0,077 |
| | | | | |  |
Сонымен
=3,66, ал критерийдiң еркiндiк дәрежесi к=s-1-r=5, мұнда берілген таңдамадағы мәліметтердің топтар саны s = 8, ал қарастырып отырған үлестірімнің параметрлерінің саны r = 2 (қалыпты үлестiрiм екi параметр арқылы анықталады). Онда кестеден (0,05; 5)=11,1. Сонымен < - нөлдiк гипотезаны жоққа шығаруға негiз жоқ.Алдыңғы 1-мысалда теориялық және эмпирикалық жиiлiктер берiлген болатын. Ендi тек эмпирикалық жиiлiктер белгiлi болғанда теориялық жиiлiктердi қалай есептеуге болатындығын көрсетелiк.
2-мысал. Интервалдық вариациялық қатар (III-тарау,1-кесте) мына түрде берiлген:
 | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 |
 | 10 | 21 | 35 | 22 | 12 |
Пирсон критерийiн қолданып маңыздылық деңгейi
болғанда сандық белгiнiң бақыланған мәндерiн пайдаланып “бас жинақ қалыпты үлестiрiммен берiлген” -деген нөлдiк болжамды тексерiңiз.Шешуі. 1.Бас жинақтың үлестiрiм заңы туралы болжам жасау үшiн, бiрiншiден, полигон және гистограмманың түрiне қараймыз. Мысалы, бас жинақ қалыпты үлестiрiммен берiлген деп болжам жасау үшiн:
а) Гистограмманың түрi Гаусс қисығының түрiне ұқсас болуы керек
б)Қалыпты үлестіріммен берілгендігін эмпирикалық ассиметрия мен эксцесстің көмегімен де анықтауға болады. Ол үшін эмпирикалық ассиметрия мен эксцесс мына теңсiздiктердi
және қанағаттандыруы керек.
Мұндағы таңдамалық асимметрия мен эксцестердің орташа квадраттық ауытқулары мына формулалар арқылы табылады
Қарастырып отырған мысал үшiн ек =0,8733,
, ал , олай болса
және .Ендi гистограммаға қарасақ (III тарау, §1), оның түрi Гаусс қисығына ұқсас. Демек, бас жинақ қалыпты үлестiрiммен берiлген деп болжам жасауға негiз бар.
-
Ендi нөлдiк болжамды тексеру үшiн Пирсон критерийiн қолданамыз. Ол үшiн
, формулаларын қолданып теориялық жиiлiктердi есептеймiз. Белгiлеу енгiзелiк
,Есептеу кестесiн құрамыз
| Интер-валдар |  |  |  |  |  |  |  |
| 0-5 | 10 | -2,23 | -1,35 | -0,4870 | -0,4115 | 0,0755 | 8 |
| 5-10 | 21 | -1,35 | -0,48 | -0,4115 | -0,1844 | 0,2277 | 23 |
| 10-15 | 35 | -0,48 | 0,39 | -0,1844 | 0,1517 | 0,3361 | 34 |
| 15-20 | 22 | 0,39 | 1,27 | 0,1517 | 0,3980 | 0,2463 | 25 |
| 20-25 |  | 1,27 | 2,14 | 0,3980 | 0,4838 | 0,0858 |  |
-
бақ есептеу үшiнде есептеу кестесiн жазған тиiмдi
 | | |  |  |  |
| 1 | 10 | 8 | 2 | 4 | 0,5 |
| 2 | 21 | 23 | -2 | 4 | 0,17 |
| 3 | 35 | 34 | 1 | 1 | 0,03 |
| 4 | 22 | 25 | -3 | 9 | 0,36 |
| 5 | 12 | 9 | 3 | 9 | 1 |
 | | | | | 1,7 |
Сонда
бақ=1,7.Ендi
маңыздылық деңгейiнде еркiндiк дәрежесi бойынша сын(0,05;2) кiтап соңындағы кестеден анықтаймыз: сын(0,05;2)=6. Осыдан бақ< сын екенiн көремiз. Демек, бас жинақтың қалыпты үлестiрiммен берiлгендiгi туралы нөлдiк болжамды қабылдамауға негiз жоқ.
1 ... 7 8 9 10 11 12 13 14 ... 22
§3. ҚАЛЫПТЫ ҮЛЕСТIРIЛГЕН БАС ЖИНАҚТЫҢ БАС
ДИСПЕРСИЯЛАРЫН САЛЫСТЫРУ
Х және У қалыпты үлестiрiлген бас жинақтардан көлемдерi n1 және n2 - ге тең болатын таңдамалар алынып, олардың түзетiлген таңдамалық дисперсиялары
және табылсын. Берiлген маңыздылық деңгейiнде мына нөлдiк болжамды тексерейiк,Ho : D(x)=D(y) (5.3.1)
H1 : D(x)>D(y) (5.3.2)
Статистикалық критерий ретiнде түзетiлген таңдамалық дисперсиялардың үлкенiнiң кiшiсiне қатынасын аламыз
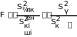(5.3.3)Бұл шама еркiндiк дәрежелерi к1=m1-1, к2=m2-1 болатын, Фишер-Снедекор үлестiрiмiмен берiлген кездейсоқ шама. Бұл жерде
-қа сәйкес таңдаманың көлемi m1, ал - қа сәйкес таңдаманың көлемi m2.Ендi берiлген деректер бойынша (5.3.3) арқылы Fбак анықтаймыз, одан кейiн Фишер-Снедекор үлестiрiмiнiң сын нүктелерi кестесiнен Fcын(,к1,к2) - ны табамыз, сонда егер Fбак < Fсын болса, онда нөлдiк болжамды қабылдамауға негiз жоқ, ал Fбак > Fсын болса нөлдiк болжам қабылданбайды.
Ескерту: Егер қарсылас болжам (5.3.2) түрiнде берiлмей, мына түрде берiлсе (H1:D(x)D(y)), онда критерийдiң сындық мәнi мына Fcын(
;к1;к2) санына тең болады.1-мысал. Бiрдей детальдар жасайтын екi автоматты
станоктардың дәлдiктерiн салыстыру мақсатымен, бiрiншi станокта өнделген детальдардың 10-ы, ал екiншiсiнде өнделгендердiң 8-i өлшенiп мынадай деректер алынды
| Хi | 1,08 | 1,10 | 1,12 | 1,14 | 1,15 | 1,25 | 1,36 | 1,38 | 1,40 | 1,42 |
| уi | 1,11 | 1,12 | 1,18 | 1,22 | 1,33 | 1,35 | 1.36 | 1,38 | | |