§1. БIР ФАКТОРЛЫҚ ДИСПЕРСИЯЛЫҚ ТАЛДАУ

Бұл жағдайда зерттелiнiп отырған Х сандық сипатты белгiсiне бiр ғана сапалық фактордың әсерiнiң бар-жоғы тексерiледi.

Дисперсиялық талдаудың таңдамаға қолданудың шарттары:

1.Таңдамалар қалыпты үлестіріммен берілген бас жинақтардан алынады;

2.Барлық жинақтардың дисперсиялары бірдей болуы керек.

Айталық қалыпты үлестіріммен берілген сандық белгіге m деңгейлі А факторы әсер етсін. Сапалық фактордың m деңгейiнiң әрқайсысында сандық сипатты белгiнiң n₁, n₂, ... , n_m байқалған мәндерi сынақ арқылы анықталады. Әдетте байқалған мәндер кестеге жазылады. Кестенің көлденең жолы бойынша фактор деңгейлері, ал тік жолдары бойынша сынақ сандары, яғни әрбір деңгейде байқалған мәндер жазылады (n₁= n₂= ,… , n_m = s ):

Сынақ номері	А факторының деңгейлері
	A1 A2 …. Ai ….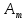
1 2 . j . s	x11 x12 ..... x1i …. x1m x21 x22 ..... x2i ….x2m xj1 xj2 ..... xji …. xjm xs1 xs2 ..... xsi …. xsm
Топтар бойынша орташалар	…. ….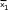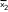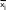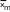

Содан кейін осы кестеден мына шамалар анықталады:

а) Сандық сипатты белгiнiң байқалған мәндерi

x_ji , i= j = (6.1.1)

б) Байқаулардың жалпы саны

(6.1.2)

в)топтық орташалар

(6.1.3)

г) Жалпылама орташа

---

(6.1.4)

д) Факторлық дисперсия

(6.1.5) е) Қалдық дисперсия
(6.1.6)

Ары қарай, егер сапалық фактор зерттелiнiп отырған көрсеткiшке әсер етпесе, онда топтық бас орташалар М( )=а_i бiрдей болулары қажет, яғни сапалық фактордың көрсеткiшке әсерiнiң бар-жоғын тексеру үшiн берiлген  маңыздылық деңгейiнде мына нөлдiк гипотезаны(болжамды) тексеру керек:

Но: а₁ = а₂= а₃=...= а_m
Ол үшiн мынадай статистикалық критерий анықталады

Бұл - еркiндiк дәрежелер к₁=m-1, к₂=n-m болатын, Фишер-Снедекор үлестiрiмiмен берiлген кездейсоқ шама. Ендi сынақ нәтижелерiне қарай отырып критерийдiң бақыланатын мәнiн F_бак есептеймiз, одан кейiн Фишер-Снедекор үлестiрiмiнiң сын нұктелерi кестесi арқылы критерийдiң сындық мәнiн

F_cын ( ;к₁;к₂) -ны анықтаймыз.

Сонда, егер F_бак< F_cын болса, онда Но гипотезасын(болжамын) жоққа шығаруға негiз жоқ болады, егер F_бак> F_cын болса, онда нөлдiк гипотеза (болжам) қабылданбайды, яғни сапалық фактордың зерттелiнiп отырған көрсеткiшке тигiзетiн әсерi мол деп айта аламыз.

1-мысал. Бiр типтес өнiм шығаратын үш фабрикадағы мамандықтары бiрдей жұмысшылардың еңбек өнiмдiлiгiне бiр сапалық фактордың (еңбектi ұйымдастырудың) тигiзетiн әсерiн =0,05 маңыздылық деңгейiнде анықтау керек. Бұл есепте сынақ арқылы анықталған жұмысшылардың еңбек өнiмдiлiгi базалық еңбек өнiмдiлiгi ретiнде қабылданған бiрлiкке қатынасы арқылы төмендегi кестеде берiлген:

Реттiк нөмiрi j	xj1	xj2	xj3
1 2 3 4 5	1,3 1,27 1,09 1,01 1,09	1,4 1,3 1,28	1,27 1,05 1,24 1,22

Шешуi: Сонымен n₁=5; n₂=3; n₃=4; n=12; m=3;

Ендi топтық орташаларды анықтаймыз:

---

Сонда жалпылама орташа



Ары қарай, факторлық дисперсияны табамыз



Ендi қалдық дисперсияны табу үшiн мына кестенi құрамыз

реттiк нөмiрi
1 2 3 4 5	1,148 1,118 -0,062 -0,142 -0,062	0,0219 0,0139 0,0038 0,0201 0,0038	0,073 -0,027 -0,047	0,0053 0,0007 0,0022	0,075 -0,145 0,045 0,025	0,0056 0,021 0,0020 0,0006
		0,0635		0,0082		0,0292

Cонымен

= (0,0635+0,0082+0,0292)=0,0112. Онда F_бак= , ал Ғ функциясының кестесінен F_cын(0,05; 2; 9) = 4,26 , осыдан F_бак< F_cын ,яғни сапалық фактор еңбек өнiмдiлiгiне әсер етпейдi деп айта аламыз.
Е С Е П Т Е Р

245.Сапалық фактордың 4 деңгейiнде жүргiзiлген сынақтардың нәтижесi төмендегi кестеде берiлген. Дисперсиялық талдау әдiсiмен 0,05

---

маңыздылық деңгейiнде топтық бас орташалардың теңдiгi туралы нөлдiк гипотезаны тексеру керек.

Реттiк нөмiрi	xj1	xj2	xj3	xj4
1 2 3 4 5	47 50 58 67	54 56 61 64 66	52 54 55	57 61

246. 14 сынақтың 7-уi сапалық фактордың бiрiншi деңгейiнде, 3-уi

екiншi деңгейiнде, ал 4 -уi үшiншi деңгейiнде жүргiзiлдi. Дисперсиялық талдау әдiсiмен  =0,01 маңыздылық деңгейiнде осы фактордың зерттелiнiп отырған көрсеткiшке әсерiнiң бар-жоғын тексеру қажет. Сынақ нәтижелерi төменгi кестеде берiлген

Реттiк нөмiрi	xj1	xj2	xj3
1 2 3 4 5 6 7	30,56 32,66 34,78 35,50 36,63 40,20 42,28	43,44 47,51 53,80	31,36 36,20 36,38 42,20

247.Сапалық фактордың 5 деңгейiнде жүргiзiлген сынақтардың нәтижесi төмендегi кестеде берiлген.  =0,05 маңыздылық деңгейiнде топтық бас орташалардың теңдiгi туралы нөлдiк гипотезаны тексеру керек.

Реттiк нөмiрi	xj1	xj2	xj3	xj4	xj5
1 2 3 4	126 133 141 147	115 119 122 128	74 87 88 94	83 87 97 106	80 80 82 86

248. Сапалық фактордың 6 деңгейiнде жүргiзiлген сынақтардың нәтижесi төмендегi кестеде берiлген.  =0,01 маңыздылық деңгейiнде топтық бас орташалардың теңдiгi туралы нөлдiк гипотезаны тексеру керек.

Реттiк нөмiрi	xj1	xj2	xj3	xj4	xj5	xj6
1 2 3 4	54 58 64 66	51 58 56 64	52 56 54 58	51 59 53 63	52 56 58 56	51 59 58

---

249. Қаладағы 5 автобус парктерінде автобустардың жүру кестесiн бұлжытпай орындауы кездейсоқ таңдамалық тәсiлмен тексерілді. Базалық бiрлiкке қатынасы бойынша берiлген осы сынақ нәтижелерi төменгi кестеде берiлген.  =0,05 маңыздылық деңгейiнде осы көрсеткiшке бiр сапалық фактордың (енбектi ұйымдастырудың) қаншалықты әсерi бар екенiн тексеру керек.

Реттiк нөмiрi	xj1	xj2	xj3	xj4	xj5
1 2 3 4 5 6	1,21 1,16 1,51 1,37	1,33 1,27 1,45 1,53 1,46 1,58	1,44 1,46 1,42 1,58 1,67	1,61 1,53 1,41 1,73	1,34 1,38 1,43

250. Сапалық фактордың 4 деңгейiнде жүргiзiлген сынақ нәтижелерi

төмендегi кестеде берiлген.  =0,05 маңыздылық деңгейiнде топтық бас орташалардың теңдiгi туралы нөлдiк гипотезаны тексеру керек.

Реттiк нөмiрi	xj1	xj2	xj3	xj4
1 2 3 4 5 6 7 8	1,6 1,61 1,65 1,68 1,70 1,71 1,8	1,58 1,64 1,64 1,70 1,75	1,46 1,55 1,60 1,62 1,64 1,66 1,74 1,82	1,51 1,52 1,53 1,60 1,68

 =0,01 маңыздылық деңгейiнде топтық бас орташалардың теңдiгi туралы гипотезаны тексерiңiз.

Реттiк нөмiрi	xj1	xj2	xj3
1 2 3 4 5 6	37 47 40 60	60 86 67 92 95 98	69 100 98

 =0,05 маңыздылық деңгейiнде төмендегi болжамды Но: a₁=a₂=a₃ тексерiңiз.

Реттiк нөмiрi	xj1	xj2	xj3
1 2 3 4	27 23 29 29	24 20 26 30	22 21 36 37

---

Смотрите также файлы

• Программа среднего профессионального образования 40. 02. 01 Право и организация социального обеспечения Дисциплина Физическая культура (2 семестр) Практическое задание 7.doc

• Родной язык Вопросы к промежуточной аттестации.docx

• Все чаще в современном обществе на различных уровнях затрагивается проблема ухудшения состояния здоровья нации.docx

• Влияние вредных привычек на организм человека.odt

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx