Файл: Ытималдытар теориясы жне математикалы статистика i тарау. Кездейсо оиалар негізгі тсініктер. Оиаларды трлері.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 770
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, 
Осыдан Х-тің әрбір мәніне У-тің бірдей шартты орташалары сәйкес келетінін көреміз. Олай болса Х пен У-тің арасында корреляциалық байланыс жоқ.
3.Бұл кесте бойынша Х пен У-тің арасында статистикалық байланыс бар екені көрініп тұр. Енді шартты орташаларды есептелік:
шартты орташаларды есептелік:
 ,
, 
Шартты орташалар әртүрлі болды. Олай болса Х пен У-тің арасында корреляциалық байланыс бар.
Анықтама 1. Егер Х кездейсоқ шамасының әрбiр мүмкiн мәнiне У кездейсоқ шамасының мүмкiн мәндерiнiң жиыны, яғни, статистикалық үлестiрiмi сәйкес келсе, онда мұндай тәуелдiлiк статистикалық тәуелдiлiк деп аталады.
Анықтама 2. Егер бiр кездейсоқ шама өзгергенде екiншi шаманың орташа мәнi өзгерсе, онда мұндай статистикалық байланыс корреляциялық байланыс деп аталады.
Сонымен Х және У кездейсоқ шамалары арасындағы корреляциялық байланыс мына формулалармен берiледi:
 , (7.1.1)
, (7.1.1)
 . (7.1.2)
. (7.1.2)
бұл жерде У кездейсоқ шамасының Х=х мәнiн қабылдағанда анықталатын шартты математикалық үмiті , ал Х кездейсоқ шамасының У=у мәнін қабылдағанда анықталатын шартты математикалық үмiті Му(Х) болады . (7.1.1), (7.1.2)- моделдiк регрессия теңдеулерi деп аталады. Оларды табу үшiн бiзге, жалпы жағдайда ( Х,У ) екi өлшемдi кездейсоқ шамасының үлестiрiм заңын бiлуiмiз керек.
, ал Х кездейсоқ шамасының У=у мәнін қабылдағанда анықталатын шартты математикалық үмiті Му(Х) болады . (7.1.1), (7.1.2)- моделдiк регрессия теңдеулерi деп аталады. Оларды табу үшiн бiзге, жалпы жағдайда ( Х,У ) екi өлшемдi кездейсоқ шамасының үлестiрiм заңын бiлуiмiз керек.
Ал іс жүзінде зерттеушi қолында шектеулi көлемдi таңдама ғана болады. Сондықтан, бұл жағдайда модельдiк регрессия теңдеулерiн (*) және (**) көмегімен жуықтап бағалау туралы ғана сөз болуы орынды. Практикада Х және У айнымалылары арасындағы статистикалық байланыстарды зерттеу үшiн корреляциялық және регрессиялық талдау тәсiлдерi қолданылады.
ғана болады. Сондықтан, бұл жағдайда модельдiк регрессия теңдеулерiн (*) және (**) көмегімен жуықтап бағалау туралы ғана сөз болуы орынды. Практикада Х және У айнымалылары арасындағы статистикалық байланыстарды зерттеу үшiн корреляциялық және регрессиялық талдау тәсiлдерi қолданылады.
§2. СЫЗЫҚТЫҚ РЕГРЕССИЯ ТЕҢДЕУЛЕРI
Айталық бiзге көлемi
-ге тең таңдамасы берiлсiн. Әдетте таңдама корреляциялық кесте түрінде беріледі:
таңдамасы берiлсiн. Әдетте таңдама корреляциялық кесте түрінде беріледі:
Әрбір хi үшін У-тің шартты орташа мәні есептеледі. Содан кейін координаталық жазықтықта (хi ,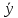 i) нүктелерін тұрғызамыз. Бұл нүктелерді өзара кесінділер арқылы қосамыз. Алынған сынық сызықтың түріне қарап У-тің Х бойынша корреляциялық байланысының түрін анықтаймыз. Х-тің У бойынша корреляциялық байланысының түрі де осы жолмен анықталады. Айталық У-тің Х бойынша корреляциялық байланысының түрі сызықтық корреляциялық байланыс түрінде анықталған болсын. Олай болса ең кіші квадраттар әдісін қолданып мына сызықтық регрессиялық теңдеулерді аламыз:
i) нүктелерін тұрғызамыз. Бұл нүктелерді өзара кесінділер арқылы қосамыз. Алынған сынық сызықтың түріне қарап У-тің Х бойынша корреляциялық байланысының түрін анықтаймыз. Х-тің У бойынша корреляциялық байланысының түрі де осы жолмен анықталады. Айталық У-тің Х бойынша корреляциялық байланысының түрі сызықтық корреляциялық байланыс түрінде анықталған болсын. Олай болса ең кіші квадраттар әдісін қолданып мына сызықтық регрессиялық теңдеулерді аламыз:
 , (7.2.1)
, (7.2.1)
 , (7.2.2)
, (7.2.2)
(7.2.1)-У-тiң Х -ке байланысты таңдамалық регрессия теңдеуi, ал (7.2.2)
Х-тiң У-ке байланысты таңдамалық регрессия теңдеуi деп аталады.
Егер - вариантасының жиiлiгi
- вариантасының жиiлiгi  , ал yj вариантасының жиiлiгi nj, сондай-ақ ,
, ал yj вариантасының жиiлiгi nj, сондай-ақ ,  қосақтарының жиiлiктерi
қосақтарының жиiлiктерi  болса, онда мынадай орташаларды анықтаймыз:
болса, онда мынадай орташаларды анықтаймыз:
 (7.2.3)
(7.2.3)
 (7.2.4)
(7.2.4)
 (7.2.5)
(7.2.5)
Ендi таңдамалық дисперсияларды табайық
 (7.2.6)
(7.2.6)
 (7.2.7)
(7.2.7)
Олай болса, мынадай шамаларды анықтауға мүмкiншiлiк туады
 (7.2.8)
(7.2.8)
 (7.2.9)
(7.2.9)
 , (7.2.10)
, (7.2.10)
Мұнда - У -тiң Х бойынша таңдамалық регрессия коэффициентi,
- У -тiң Х бойынша таңдамалық регрессия коэффициентi,  - Х -тiң У бойынша таңдамалық коэффициентi, ал
- Х -тiң У бойынша таңдамалық коэффициентi, ал  таңдамалық корреляция коэффициентi деп аталады.
таңдамалық корреляция коэффициентi деп аталады.
Корреляция коэффициентiнiң негiзгi қасиеттерi:
а) ;
;
б) Егер
болса, онда корреляциялық байланыс сызықтық функционалдық тәуелдiлiк болады.
в) Егер болса, онда сызықтық корреляциялық байланыс жоқ, бiрақ корреляциялық немесе статистикалық байланыстар басқаша түрде болуы мүмкiн.
болса, онда сызықтық корреляциялық байланыс жоқ, бiрақ корреляциялық немесе статистикалық байланыстар басқаша түрде болуы мүмкiн.
г)Сондай-ақ, - бас корреляция коэффициентi
- бас корреляция коэффициентi  - ның нүктелiк бағасы болады.
- ның нүктелiк бағасы болады.
1-мысал. 50 бiр типтес кәсiпорындар үшiн тәулiктiк өнiм шығарылымының У (тонна) негiзгi өндiрiстiк қорлардан Х (млн.теңге) тәуелдiлiгiн қарастырайық:
7.1. кесте
У пен Х арасында сызықтық корреляциялық байланыс бар деп жорамалдап, таңдамалық регрессия теңдеулерiн құрыңыз.
Шешуi: (7.2.3)-(7.2.10) формулалары арқылы барлық шамаларды анықтаймыз.

Осы табылған мәндердi (7.2.1), (7.2.2) теңдеулерiне қойсақ мына регрессия теңдеулерiн аламыз
 (7.2.11)
(7.2.11)
 (7.2.12)
(7.2.12)
Осы теңдеулерден мынаны байқаймыз: Егер негiзгi өндiрiс қорларын 1 млн. теңгеге арттырсақ, онда тәулiктiк өнiм шығарылымы орта есеппен 0,366 тоннаға өседi, ал тәулiктiк өнiм шығарылымын 1 тоннаға өсiру үшiн негiзгi өндiрiс қорларын орта есеппен 0,382 млн.теңгеге арттыру керек.
Сонымен, Х және У шамалары арасында сызықтық корреляциялық байланыс бар деймiз, бұл байланыстың қаншалықты тығыз екендiгiн анықтайды.
анықтайды.
Осыдан Х-тің әрбір мәніне У-тің бірдей шартты орташалары сәйкес келетінін көреміз. Олай болса Х пен У-тің арасында корреляциалық байланыс жоқ.
3.Бұл кесте бойынша Х пен У-тің арасында статистикалық байланыс бар екені көрініп тұр. Енді
Шартты орташалар әртүрлі болды. Олай болса Х пен У-тің арасында корреляциалық байланыс бар.
Анықтама 1. Егер Х кездейсоқ шамасының әрбiр мүмкiн мәнiне У кездейсоқ шамасының мүмкiн мәндерiнiң жиыны, яғни, статистикалық үлестiрiмi сәйкес келсе, онда мұндай тәуелдiлiк статистикалық тәуелдiлiк деп аталады.
Анықтама 2. Егер бiр кездейсоқ шама өзгергенде екiншi шаманың орташа мәнi өзгерсе, онда мұндай статистикалық байланыс корреляциялық байланыс деп аталады.
Сонымен Х және У кездейсоқ шамалары арасындағы корреляциялық байланыс мына формулалармен берiледi:
бұл жерде У кездейсоқ шамасының Х=х мәнiн қабылдағанда анықталатын шартты математикалық үмiті
Ал іс жүзінде зерттеушi қолында шектеулi көлемдi таңдама
§2. СЫЗЫҚТЫҚ РЕГРЕССИЯ ТЕҢДЕУЛЕРI
Айталық бiзге көлемi
-ге тең
| У Х | У1 | у2 | ... | уj | ... | уn | mх |
| х1 | m11 | m12 | ... | m1j | ... | m1n | m х1 |
| х2 | m21 | m22 | ... | m2j | ... | m2n | m х2 |
| | ... | ... | ... | ... | ... | ... | ... |
| хi | mi1 | mi2 | ... | mij | ... | min | m хi |
| | ... | ... | ... | ... | ... | ... | ... |
| хm | mm1 | mm2 | ... | mmj | ... | mmn | m хm |
| mу | m у1 | m у2 | ... | m уj | ... | m уn | n |
Әрбір хi үшін У-тің шартты орташа мәні есептеледі. Содан кейін координаталық жазықтықта (хi ,
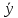 i) нүктелерін тұрғызамыз. Бұл нүктелерді өзара кесінділер арқылы қосамыз. Алынған сынық сызықтың түріне қарап У-тің Х бойынша корреляциялық байланысының түрін анықтаймыз. Х-тің У бойынша корреляциялық байланысының түрі де осы жолмен анықталады. Айталық У-тің Х бойынша корреляциялық байланысының түрі сызықтық корреляциялық байланыс түрінде анықталған болсын. Олай болса ең кіші квадраттар әдісін қолданып мына сызықтық регрессиялық теңдеулерді аламыз:
i) нүктелерін тұрғызамыз. Бұл нүктелерді өзара кесінділер арқылы қосамыз. Алынған сынық сызықтың түріне қарап У-тің Х бойынша корреляциялық байланысының түрін анықтаймыз. Х-тің У бойынша корреляциялық байланысының түрі де осы жолмен анықталады. Айталық У-тің Х бойынша корреляциялық байланысының түрі сызықтық корреляциялық байланыс түрінде анықталған болсын. Олай болса ең кіші квадраттар әдісін қолданып мына сызықтық регрессиялық теңдеулерді аламыз:
(7.2.1)-У-тiң Х -ке байланысты таңдамалық регрессия теңдеуi, ал (7.2.2)
Х-тiң У-ке байланысты таңдамалық регрессия теңдеуi деп аталады.
Егер
Ендi таңдамалық дисперсияларды табайық
Олай болса, мынадай шамаларды анықтауға мүмкiншiлiк туады
Мұнда
Корреляция коэффициентiнiң негiзгi қасиеттерi:
а)
б) Егер
болса, онда корреляциялық байланыс сызықтық функционалдық тәуелдiлiк болады.
в) Егер
г)Сондай-ақ,
1-мысал. 50 бiр типтес кәсiпорындар үшiн тәулiктiк өнiм шығарылымының У (тонна) негiзгi өндiрiстiк қорлардан Х (млн.теңге) тәуелдiлiгiн қарастырайық:
7.1. кесте
| Х У | 9 | 10 | 13 | 15 | nj |
| 10 | 8 | 10 | | | 18 |
| 12 | 2 | 5 | 13 | | 20 |
| 20 | | | 7 | 5 | 12 |
| ni | 10 | 15 | 20 | 5 | n=50 |
У пен Х арасында сызықтық корреляциялық байланыс бар деп жорамалдап, таңдамалық регрессия теңдеулерiн құрыңыз.
Шешуi: (7.2.3)-(7.2.10) формулалары арқылы барлық шамаларды анықтаймыз.

Осы табылған мәндердi (7.2.1), (7.2.2) теңдеулерiне қойсақ мына регрессия теңдеулерiн аламыз
Осы теңдеулерден мынаны байқаймыз: Егер негiзгi өндiрiс қорларын 1 млн. теңгеге арттырсақ, онда тәулiктiк өнiм шығарылымы орта есеппен 0,366 тоннаға өседi, ал тәулiктiк өнiм шығарылымын 1 тоннаға өсiру үшiн негiзгi өндiрiс қорларын орта есеппен 0,382 млн.теңгеге арттыру керек.
Сонымен, Х және У шамалары арасында сызықтық корреляциялық байланыс бар деймiз, бұл байланыстың қаншалықты тығыз екендiгiн