58. Дайын бұйымдар қоймасындағы бұйымдардың 70% - тi бiрiншi автоматта, ал 30% - тi екiншi автоматта дайындалған. Бiрiншi автоматтың сапалы бұйымдар дайындауының ықтималдығы 0,98, ал екiншiсiнiкi - 0,95-ке тең. Алынған кез-келген бiр бұйым сапасыз болып шықты. Осы бұйымның бiрiншi автоматта дайындалғандығының ықтималдығы қандай?

59. Группада 10 студент бар. Олардың үшеуi емтиханға өте жақсы, төртеуi - жақсы, екеуi - орташа және бiреуi - нашар дайындалған. Емтихандық билеттерде әртүрлi 20 сұрақ берiлген. Өте жақсы дайындалған студент барлық 20 сұраққа, жақсы жайындалған - 16 сұраққа, орташа дайындалған - 10 сұраққа, нашар дайындалған - 5 сұраққа толық жауап бере алады. Кез-келген бiр студент берiлген үш сұраққа толық жауап бердi. Жауап берген студенттiң: а) өте жақсы дайындалғандығының; б) жақсы дайындалғандығының; в) орташа дайындалғандығының; г) нашар дайындалғандығының ықтималдықтарын табу керек;

Нұсқау: Мына гипотезаларды енгiзген жөн:

B₁-өте жақсы дайындалған студент; B₂- жақсы дайындалған студент; B₃ орташа дайындалған студент; B₄- нашар дайындалған студент;

Сондай-ақ , А - кезкелген студент үш сұраққа толық жауап бердi.

Сонда мысал үшiн т.c.c.

60. Бiрiншi урнада 1 ақ, 2 қара, ал екiншiсiнде - 3 ақ, 4 қара шарлар бар. Кез-келген урнадан кез-келген бiр шар алынды, ол ақ шар болып шықты. Сол урнадан алынған келесi шардың да ақ шар болғандығының ықтималдығын табу керек.

Нұсқау: В₁ - шар бiрiншi урнадан алынды; В₂ - шар екiншi урнадан алынды; В₃ - бiрiншi рет ақ шар алынды; В₄ - екiншi рет ақ шар алынды. А-кез келген урнада бiрiншi рет алынған шар ақ болды; В-кез келген урнадан екiншi рет алынған шар ақ болды.

Әуелi , тауып алу керек. Сонда iздеп отырған ықтималдық



61. 18 атқыштың бесеуi нысанаға 0,8 ықтималдықпен, жетеуi - 0,7, төртеуi - 0,6, екеуi - 0,5 ықтималдықпен тигiзедi. Кез келген атқыш атыс жасады да тигiзе алмады. Атыс жасаған атқыш қайсы топтан болғандығының ықтималдығын табу керек.

Нұсқау: атқыш бiрiншi, екiншi, үшiншi, төртiншi группадан екендiгiнiң ықтималдықтарын тауып, оларды салыстыру керек.

---

§4. ТӘУЕЛСIЗ СЫНАҚТАР ТIЗБЕГI
Айталық сынақтар сериясы жүргізілсін. Егер А оқиғасының пайда болуы оның алдыңғы сынақтарда пайда болғанына немесе пайда болмағанына байланысты болмаса, онда ондай сынақтар А оқиғасы бойынша тәуелсіз сынақтар деп аталады.

Екi ғана нәтижесi бар ("А оқиғасы пайда болады" және "А оқиғасы пайда болмайды") тәуелсiз сынақтарды қарастыралық. Мұндай сынақтарға теңге лақтыру, бұйымның сапалылығын , жарамдылығын тексеру т.б. сынақтар жатады.

Сонымен аталған екi нәтиженi "А оқиғасы пайда болады" және "А оқиғасы пайда болмайды" деп атаcақ, сонда осы екi оқиғаның бiр-бiрiне қарама-қарсы екенiн ескерiп, сәйкес ықтималдықтарын P(A)=p және 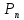деп аламыз. Мұнда әрбір сынақта А оқиғасының ықтималдығы тұрақты болса, онда осындай екі нәтижелі сынақтар үшін Бернулли схемасы орынды деп айтады. Енді осы тәуелсіз сынақтарда А оқиғасының тура к рет пайда болуының ықтималдығы есептелік. Осы ықтималдықты былай белгілейді (k). Тәуелсіз сынақтарда А оқиғасы тура к рет әртүрлі варианттармен пайда болуы мүмкін. Мысалы, 3 тәуелсіз сынақ жүргізілген болсын. Сонда А оқиғасының тура 2 рет пайда болуына төмендегідей варианттар сәйкес келеді: 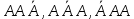, яғни А оқиғасы алғашқы екі сынақта пайда болуы мүмкін, немесе бірінші және үшінші сынақтарда, немесе екінші және үшінші сынақтарда пайда болуы мүмкін. Осыдан бұл оқиғалардың үйлесімсіз екенін ескеріп және ықтималдықтарды қосу, көбейту теоремаларын пайдаланып 3 тәуелсіз сынақтарда оқиғаның тура 2 рет пайда болуының ықтималдығын табамыз:

.
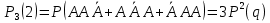БЕРНУЛЛИ ФОРМУЛАСЫ
Жалпы жағдайда тәуелсiз n сынақтарда (Бернулли схемасы бойынша) тұрақты ықтималдықпен пайда болатын болатын А оқиғасының тура к рет пайда болуының ықтималдығы Бернулли формуласымен есептеледi:
(1.4.1)

Мұндағы p=P(A), q=1-p=

---

. Бұл формуланы кейде биномдық деп те атайды. Қарастырылған мысалда n=3, k=2, яғни (1.4.1) формуласы бойынша

Р₃(2)=3р²q

Егер n тәуелсіз сынақтарда оқиғаның m₀ рет пайда болуына сәйкес келетін ықтималдық ең үлкен болса немесе оқиғаның басқа пайда болу сандарының ықтималдықтарынан кем болмаса, онда m₀ оқиғаның пайда болуының ең ықтималды саны деп аталады.

Осы сынақтарда А оқиғасының ең ықтималды m₀ рет пайда болуы мына теңсiздiктен анықталады:

(1.4.2)

Егер np-q- бүтiн сан болса, онда m₀-дiң екi бүтiн мәнi болады, ал np-q- бүтiн сан болмаса, онда m₀- дiң бiр ғана бүтiн мәнi болады.

Бернулли формуласын пайдаланып мына оқиғалардың ықтималдығын анықтауға болады:

1. Тәуелсiз n сынақтарда А оқиғасының к реттен кем пайда болатындығының ықтималдығы:

(1.4.3)

2. к реттен артық болуының ықтималдығы:

(1.4.4)

3. Кем дегенде к рет пайда болуының ықтималдығы:

(1.4.5)

4. к реттен артық емес пайда болуының ықтималдығы

(1.4.6)

Бернулли схемасы бойынша тәуелсiз сынақтарда, А оқиғасының ең болмағанда бiр рет пайда болуының ықтималдығы мына формуламен анықталады:

P=1-qⁿ (1.4.7)

1-мысал. Шахмат ойнау шеберлiгi тең екi шахматшы ойын көрсетуде. Тең аяқтаған ойынды есептемегенде:

1.Төрт партияның үшеуiн ұту мен сегiз партияның бесеуiн ұтудың ықтималдықтарын табу керек. Қайсысының ықтималдығы жоғары?

2.Төрт партиядан кем дегенде үш партия ұту мен сегiз партиядан кем дегенде 5 партия ұтудың ықтималдықтарын табу керек. Қайсысының ықтималдықтары жоғары?

Шешуi: Ойнау шеберлiгi тең болғандықтан олардың әрбiр партияда ұту ықтималдықтары 0,5 тең.

1. Төрт партиядан үш ұтыстың ықтималдығы Бернулли формуласы (1.4.1) бойынша



Сегiз партияда 5 ұтыстың ықтималдығы

---

Осыдан, яғни төрт партиядан үш ұтыстың ықтималдығы, сегiз партиядан 5 ұтыстың ықтималдығынан жоғары.

2. Төрт партиядан кем дегенде үш ұтыстың ықтималдығы


Сегiз партиядан кем дегенде 5 партия ұтудың ықтималдығы


Осыдан 93/256 > 5/16, яғни сегiз партиядан кем дегенде бес ұтыстың ықтималдығы, төрт партиядан кем дегенде 3 партия ұтыстың ықтималдығынан жоғары.

Ескерту: Егер Бернулли схемасында сынақтар саны үлкен болса, онда Бернулли формуласын пайдалану үлкен арифметикалық есептеулерге келтiредi. Сондықтан бұл жағдайда жуықтап есептеу формулаларын қолданады.

Егерде P(A)=p мәнi 0,5-тiң маңайында болса, онда Муавр-Лапластың локалдық және интегралдық жуықтау формулалары қолданылады.

МУАВР–ЛАПЛАСТЫҚ ЛОКАЛДЫҚ ТЕОРЕМАСЫ
Тәуелсiз n сынақтарда ықтималдығы тұрақты А оқиғасының тура к рет пайда болуының ықтималдығы мына формула бойынша жуықтап есептеледi:
, , (1.4.8)
МУАВР-ЛАПЛАСТЫҚ ИНТЕГРАЛДЫҚ ТЕОРЕМАСЫ

Тәуелсiз n сынақтарда ықтималдығы тұрақты А оқиғасының к₁- ден емес к₂- ге дейін пайда болуының ықтималдығы мына формула бойынша жуықтап есептеледi:

(1.4.9)
Мұндағы (х), Ф(х_i) функцияларының мәндерiнiң кестесi бөлек келтiрiлген. Сондай-ақ, (1.4.8) формуладан (х) жұп функция, ал (1.4.9) формуладан Ф(х_i) тақ функция екенін көреміз.

Муавр-Лапластың (1.4.9) формуласын пайдаланып тәуелсiз сынақтарда А оқиғасының ықтималдығының салыстырмалы жиiлiктен ауытқуының абсолют шамасының ықтималдығы мына формула арқылы табылады:

---

(1.4.10)

Егерде P(A)=p мәнi 0,5 -тен едәуiр кiшi болса, онда басқа жуықтау формуласы - Пуассон формуласы қолданылады:
, =np (1.4.11)

2-мысал. Тәуелсiз 600 сынақтарда тұрақты p=0,4 ықтималдықпен пайда болатын оқиғаның тура 228 рет пайда болуының ықтималдығын табу керек.

Шешуi: Бұл есептiң дәл шешуi Бернулли формуласымен табылады, бiрақта бұл есепте сынақтар саны n=600 аса үлкен. Сондықтан Муавр-Лапластың локалдық формуласын пайдаланамыз. Ол үшiн әуелi х -тiң мәнiн табалық


Сонда (-1)0,242,


3-мысал. Мергеннiң нысанаға тигiзуiнiң ықтималдығы 0,75 - ке тең.

1.100 атыста мына оқиғалардың ықтималдықтарын табу керек.

а) нысанаға 71- ден кем емес 80- нен артық емес рет дәл тидi,

б) нысанаға 70 - тен артық емес рет дәл тидi,

2.Тәуелсiз 400 атыста салыстырмалы жиiлiктiң ықтималдықтан p=0,75 ауытқуының абсолют шамасы 0,035-тен кем болатындығының ықтималдығын табу керек.

3.Салыстырмалы жиiлiктiң оқиғаның ықтималдығынан p=0,75 ауытқуының абсолют шамасы 0,035 - тен кем болатындығының ықтималдығы 0,95 - ке тең болуы үшiн қанша тәуелсiз атыс жасау керек?

4.Тәуелсiз 100 атыста нысанаға дәл тиген ең ықтималды атыс санын табу керек.

Шешуi: 1. Бұл жерде (1.4.9) формуланы қолданамыз:

а) к₁=71 к₂=80 n=100 p=0,75 q=0,25
;
Сонда P₁₀₀(71,80)

б) к₁=0 к₂=70 n=100 p=0,75 q=0,25



P₁₀₀(0,70)
2. Бұл жерде (1.4.10) формуланы қолданамыз:

n=400, p=0,75, q=0,25, =0,035


Сонда
3. Есептiң шарты бойынша

---

Смотрите также файлы

• Программа среднего профессионального образования 40. 02. 01 Право и организация социального обеспечения Дисциплина Физическая культура (2 семестр) Практическое задание 7.doc

• Родной язык Вопросы к промежуточной аттестации.docx

• Все чаще в современном обществе на различных уровнях затрагивается проблема ухудшения состояния здоровья нации.docx

• Влияние вредных привычек на организм человека.odt

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx