Файл: Федеральное агентство по образованию иркутский государственный технический университет.doc

Высота треугольной фермы в середине пролета определяется в зависимости от пролета и уклона верхнего пояса и может достигать значительных размеров.

5.2. Порядок расчета стропильных ферм

Проектирование фермы начинают с ее компоновки. На этой стадии выбирают статическую схему и очертание фермы, назначают вид решетки и определяют генеральные размеры. Затем производят статический расчет фермы, подбор сечений элементов фермы, расчет и конструирование ее узлов.

5.2.1. Определение нагрузок на ферму

Стропильные фермы рассчитываются на нагрузки, передающиеся на них в виде сосредоточенных сил в узлах: постоянную – от веса кровли, конструкций подвесного потолка, собственного веса фермы со связями и др.; временные – от снега, а также от ветра (при уклонах кровли более 30^о), подвесного подъемно-транспортного оборудования (при его наличии) и других возможных технологических нагрузок.

Равномерно распределенная нагрузка подсчитывается сначала на 1 м² площади, затем по грузовой площади находится сосредоточенная сила, действующая на каждый узел.

При возможном загружении фермы снеговой нагрузкой на половине пролета может измениться знак усилия с «плюса» на «минус» в средних малонагруженных элементах решетки. В практических расчетах такие элементы принимаются конструктивно по предельно допустимой гибкости как сжатые (независимо от знака усилия).

При жестком сопряжении ригеля с колонной ферма в составе рамы испытывает воздействие рамных опорных моментов и продольной силы (усилия от распора) N_р, передающейся при восходящем опорном раскосе на нижний пояс фермы.

Значение опорных моментов М_л и М_п принимаются при одной и той же комбинации нагрузок. При определении усилий в стержнях фермы опорные моменты заменяются двумя парами горизонтальных сил, приложенных на опорах:

Н₁ = М_л/h_о и Н₂ = М_п/h_о,

где h_о – высота фермы на опоре по центрам тяжести поясов.
5.2.2. Определение усилий в стержнях фермы

При работе ферм с элементами из уголков или тавров принимается допущение, что все стержни соединены в узлах шарнирно

---

, оси всех стержней прямолинейны, расположены в одной плоскости и пересекаются в узле в одной точке.

После предварительного определения опорных реакций фермы, усилия в элементах стропильных ферм от неподвижной нагрузки определяются, как правило, графическим методом – путем построения диаграммы Максвелла-Кремоны или аналитическим методом отдельно для всех загружений. Для симметричного загружения диаграмма усилий строится для половины фермы.

При наличии опорных моментов строится диаграмма усилий от единичного момента М₁, приложенного к левой опоре. Зеркальное отображение этих усилий дает значение усилий в стержнях фермы от единичного момента,

приложенного к правой опоре. Единичный момент заменяется эквивалентной парой сил Н = М₁/h_о с плечом h_о. Умножая значение усилий в стержнях фермы от единичных моментов соответственно на М_л и М_п, получаем фактические усилия в стержнях.

Усилия от каждого загружения оформляются в табличной форме (табл. 5.1).

Таблица 5.1

Расчетные усилия в стержнях фермы, кН (форма таблицы)

Элемент фермы	Обозна-чение стержня	Постоян-ная нагрузка	Сне-говая		Опорные моменты			Расчетное усилие
			ψ = 1,0	ψ = 0,9	Mл = 1	Mп = 1	Mл =…Mп =…	Номера загру-жения	Значе-ние

Лучше всего расчет ферм выполнить на ЭВМ, воспользовавшись любой из известных программ.

Для подбора сечений элементов ферм необходимо получить для каждого элемента максимально возможное усилие при самом невыгодном сочетании нагрузок.

При приложении нагрузок вне узлов фермы ее пояса рассчитываются на совместное действие продольных усилий и изгибающего момента как неразрезные балки, опирающиеся на узлы ферм. Значение изгибающего момента от сосредоточенной силы

---

F приближенно определяется по формуле

М = 0,9Fd/4,

где коэффициент 0,9 учитывает неразрезность пояса;

d– длина панели.

5.2.3. Определение расчетных длин и предельных гибкостей

стержней фермы

В критическом состоянии потеря устойчивости при продольном изгибе сжатых стержней возможна в любом направлении (в плоскости фермы или из ее плоскости).

Предельная гибкость для сжатых элементов ферм и связей зависит от назначения стержня, степени его загруженности, оцениваемой коэффициентом

α = N/(φAR_yγ_c),

где N– расчетное усилие;

φAR_yγ_c – несущая способность стержня (табл. 5.2).
Таблица 5.2.

Предельные гибкости сжатых элементов

Элементы конструкций	Предельная гибкость λu
Пояса, опорные раскосы и стойки плоских ферм, передающие опорные реакции	180-60α
Верхние пояса ферм, незакрепленные в процессе монтажа (предельную гибкость после завершения монтажа следует принимать по поз.1)	220
Основные колонны	180-60α
Второстепенные колонны (стойки фахверка, фонарей и т.п.), элементы решетки колонн, элементы вертикальных связей между колоннами (ниже подкрановых балок)	210-60α
Элементы связей, кроме указанных в поз. 4, а также стержни, служащие для уменьшения расчетной длины сжатых стержней, и другие ненагруженные элементы	200

Обозначение: – коэффициент, принимаемый не менее 0,5 (в необходимых случаях вместо φ следует применять φ_е).

Гибкие растянутые стержни могут провисать под действием собственного веса, легко повреждаться при транспортировании и монтаже, а при действии динамических нагрузок вибрировать, поэтому их гибкость тоже ограничена (табл. 5.3). При статических нагрузках гибкость растянутых элементов ограничивается только в вертикальной плоскости.

Гибкость стержня определяется его расчетной длиной l_еf (табл. 5.4) и радиусом инерции сечения i:

λ =

---

l_еf/i.

Расчетные длины стержней определяются:

– в плоскости фермы

l_х = μl;

– из плоскости фермы

l_y = μl₁,

где μ – коэффициент приведения длины к расчетной, зависящий от способов закрепления концов стержня;

l – геометрическая длина элемента (расстояние между центрами узлов);

l₁ – расстояние между узлами, закрепленными от смещения из плоскости фермы (прогонами, специальными связями, жесткими плитами покрытий, прикрепленными к поясу сварными швами или болтами, и т.п.).

Таблица 5.3

Предельные гибкости растянутых элементов

Элементы конструкции	Предельная гибкость λu при воздействии на конструкцию нагрузок
	динамических, приложенных непосредственно к конструкции	статических	от кранов
Пояса и опорные раскосы плоских ферм (включая тормозные фермы) и структурных конструкций	250	400	250
Элементы ферм и структурных конструкций, кроме указанных в поз.1	350	400	300
Нижние пояса подкрановых балок и ферм	–	–	150

П р и м е ч а н и я: 1. В конструкциях, не подвергающихся динамическим воздействиям, гибкость растянутых элементов следует проверить только в вертикальных плоскостях.

2. Для растянутых элементов, в которых при неблагоприятном расположении нагрузки может изменяться знак усилия, предельную гибкость следует принимать как для сжатых элементов, при этом соединительные прокладки в составных элементах необходимо устанавливать не реже чем через 40i.

Особое внимание обращается на устойчивость верхнего пояса в пределах фонаря, где отсутствует кровельный настил или прогоны. Здесь для раскрепления узлов из плоскости фермы предусматриваются распорки (обязательные в коньковом узле). В процессе монтажа (до укладки плит покрытия или прогонов) распорка призвана обеспечить гибкость пояса λ_у ≤ λ_u= 220.

Таблица 5.4

Расчетные длины стержней ферм

Направление продольного изгиба	Расчетная длина lef
	пояса	опорные раскосы и опорные стойки	прочие элементы решетки
В плоскости фермы: а) для ферм, кроме указанных в поз. 1, б б) для ферм из одиночных уголков и ферм с прикреплением элементов решетки к поясам впритык	l	l	0,8l
	l	l	0,9l
Перпендикулярно плоскости фермы (из плоскости фермы): а) для ферм, кроме указанных в поз. 2, б б) для ферм с поясами из замкнутых профилей с прикреплением элементов решетки к поясам впритык	l1	l1	l1
	l	l	0,9l

---

Обозначения:

l – геометрическая длина элемента (расстояние между центрами узлов) в плоскости фермы;

l₁ – расстояние между узлами, закрепленными от смещения из плоскости фермы (прогонами, специальными связями, жесткими плитами покрытий, прикрепленными к поясу сварными швами или болтами, и т.п.).

5.2.4. Выбор типа сечений стержней фермы

Для центрально-сжатых стержней, рассчитываемых на устойчивость, основным требованием при конструировании элемента является стремление к обеспечению равноустойчивости стержня относительно осей х-х и у-у:

λ_х= (l_х/i_х)= λ_у= (l_у/i_у).

Наиболее распространенными и традиционными являются тавровые сечения стержней ферм, выполненные из двух уголков.

Такие сечения имеют большой диапазон площадей, удобны для конструирования узлов на фасонках и прикрепления примыкающих к фермам конструкций (прогонов, кровельных плит, связей). Существенными недостатками такой конструктивной формы являются: большое количество элементов с различными типоразмерами, значительный расход стали на фасонки и прокладки, высокая трудоемкость изготовления и наличие щели между уголками, что способствует коррозии.

Использование для поясов ферм тавров позволяет значительно упростить узлы.

Тавровое сечение может выполняться из двух равнополочных (i_у ≈ 1,33i_х) или неравнополочных уголков. Неравнополочные уголки можно составлять узкими полками (i_у ≈ 2i_х) или более широкими полками (i_у≈ i_х) в зависимости от расчетных длин элементов при расчете в двух направлениях, обеспечивая равноустойчивость сечения (см. табл. 5.5).

Таблица 5.5

Приближенные значения радиусов сечений элементов из уголков

Радиусы инерции	Сечение элементов
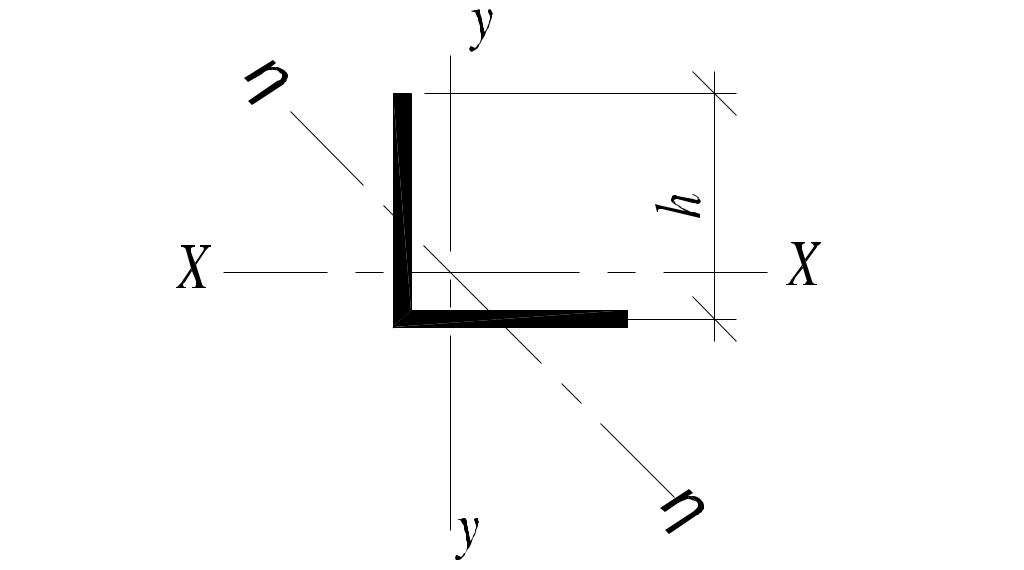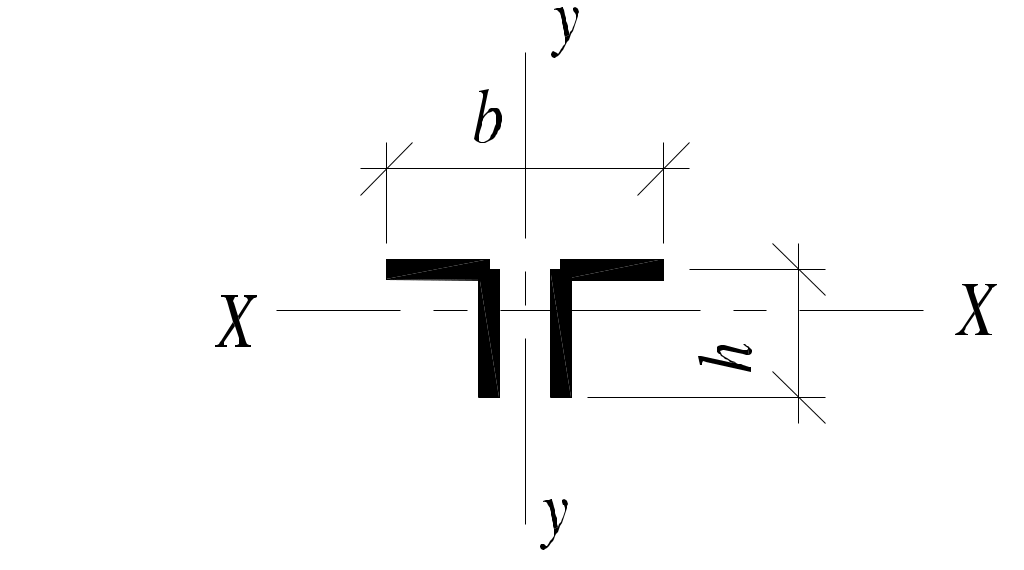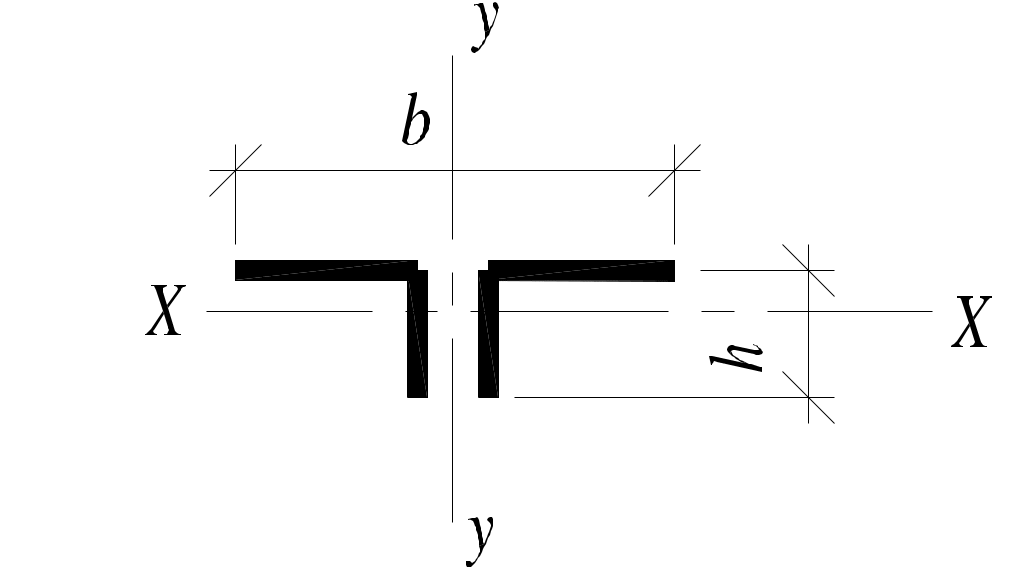rxи rη ry	rη= 0,195 h rx =ry= 0,3 h	rx= 0,3 h ry= 0,2 b	0,28h 0,24b
Радиусы инерции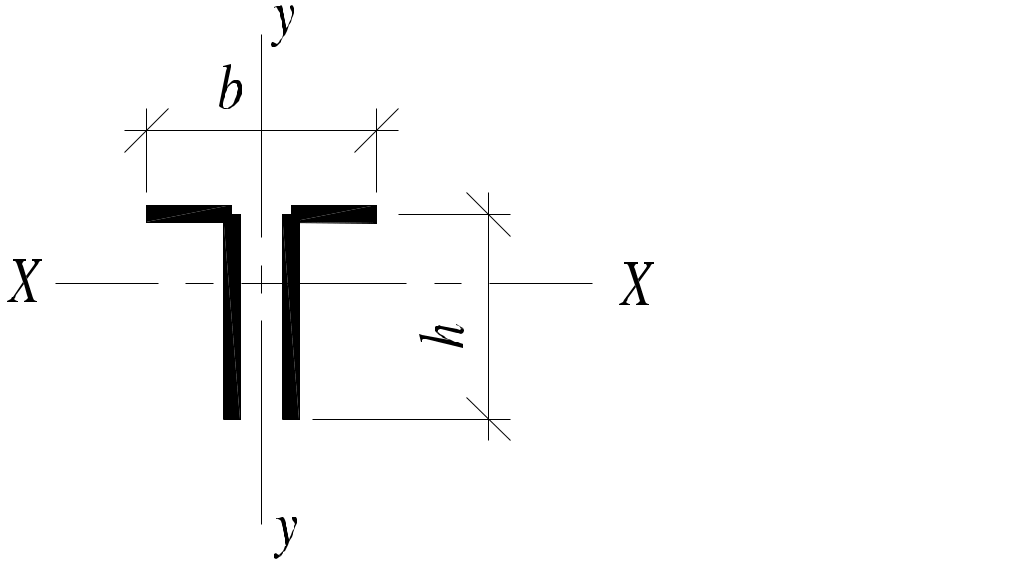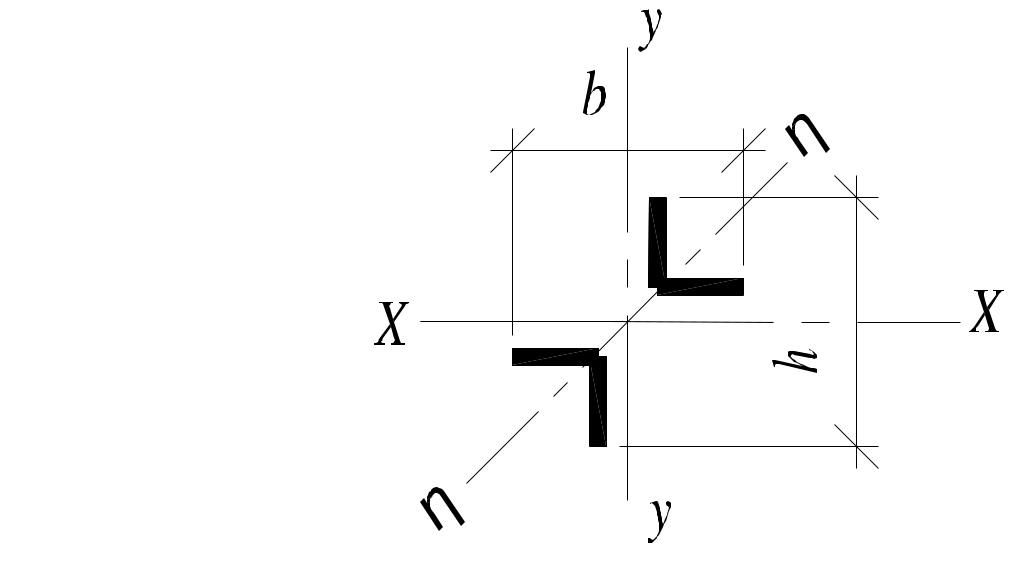
rxи rη ry	0,32 h 0,2 b	rη= 0,185 h 0,21 h	0,3 h 0,17 b

---