Файл: Федеральное агентство по образованию иркутский государственный технический университет.doc

Рис. 5.3. Расчетная схема и сечение пояса

Определяем изгибающий момент в середине панели пояса

M= 0,9Fd/4 = 0,9 ∙ 55 ∙ 300 / 4 = 3712, 5 кН∙см.

Эксцентриситет

е = M/N= 3712,15 / 1300 = 2,86 см.

Расчет на устойчивость внецентренно-сжатых и сжато-изгибаемых элементов выполняется как в плоскости действия момента (плоская форма потери устойчивости), так и из плоскости действия момента (изгибно-крутильная форма потери устойчивости).

Расчет таких элементов постоянного сечения в плоскости действия момента, совпадающей с плоскостью симметрии, производится по формуле



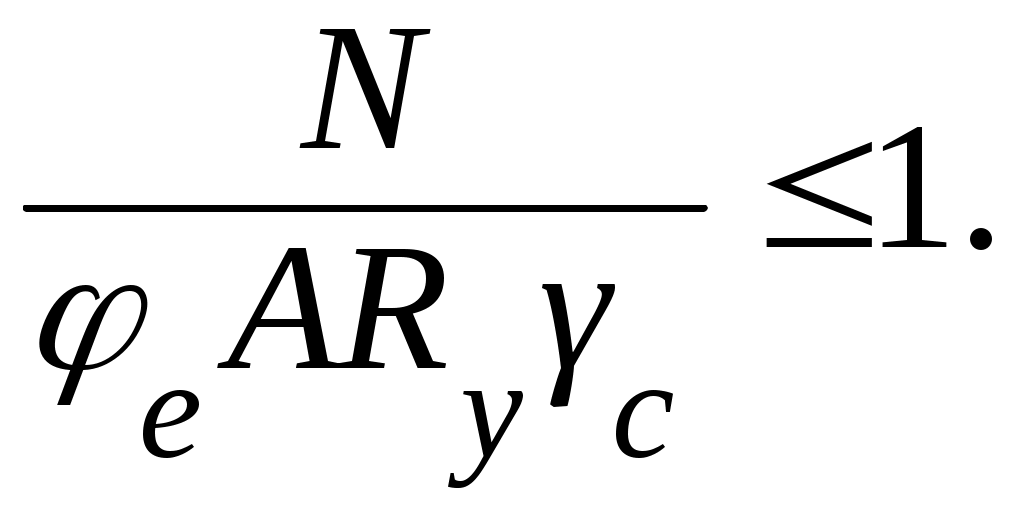
Таблица 5.7

Коэффициент влияния формы сечения η

Схема сечения		Значение h при
		0 £ £ 5		> 5
		0,1£ m £ 5	5 < m £ 20	0,1£ m £ 5	5 < m £ 20
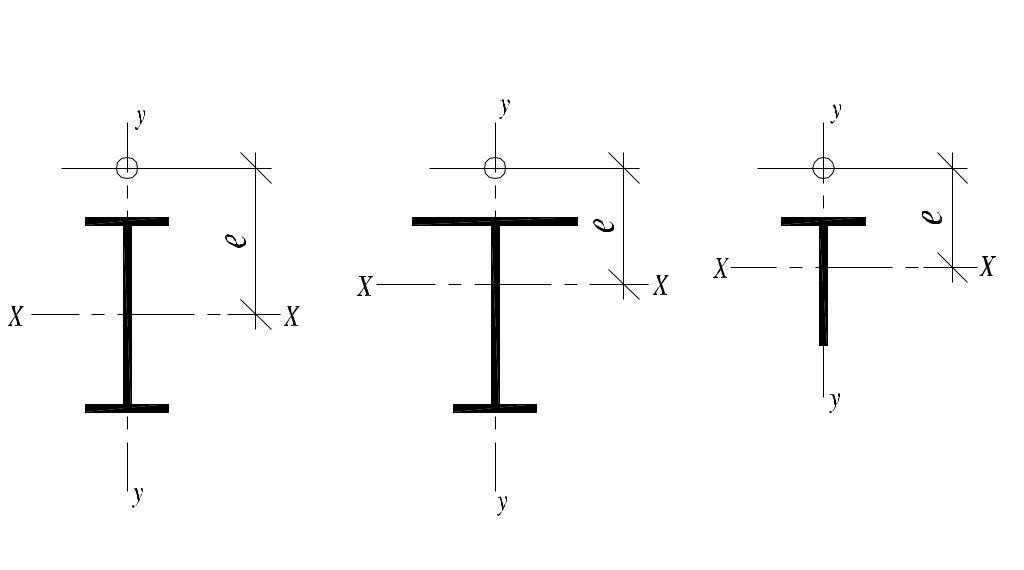	0,25	(1,45–0,05m) – – 0,01(5–m)	1 ,2	1,2
	0,5	(1,75-0,1m) – – 0,02(5–m)	1,25	1,25
	³1,0	(1,90-0,1m) – – 0,02(6–m)	1,4 – - 0,02	1,3
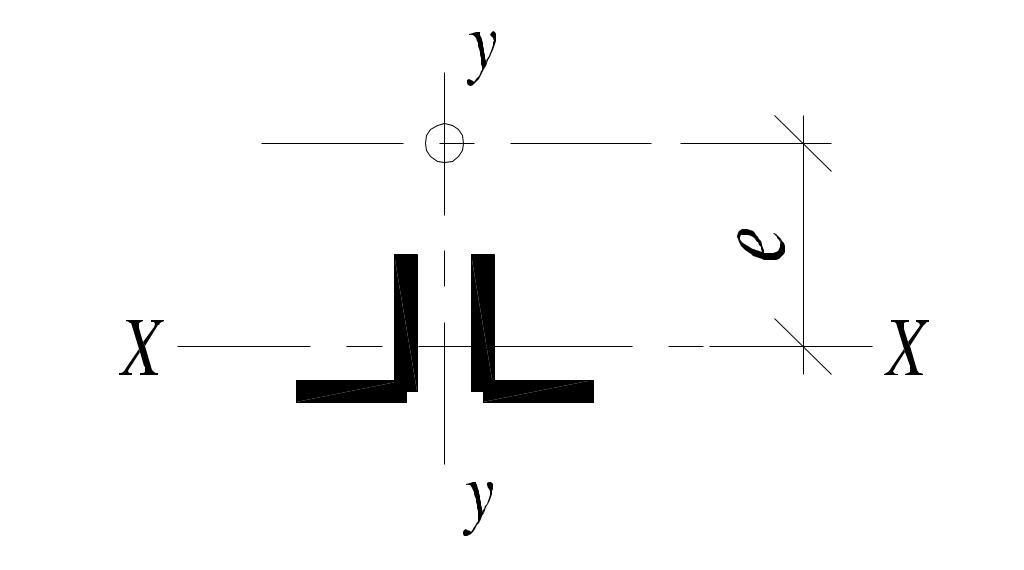	0,5	(1,25–0,05m) – – 0,01(5–m)	1,0	1,0
	³1,0	(1,5–0,1m) – – 0,02(5–m)	1,0	1,0
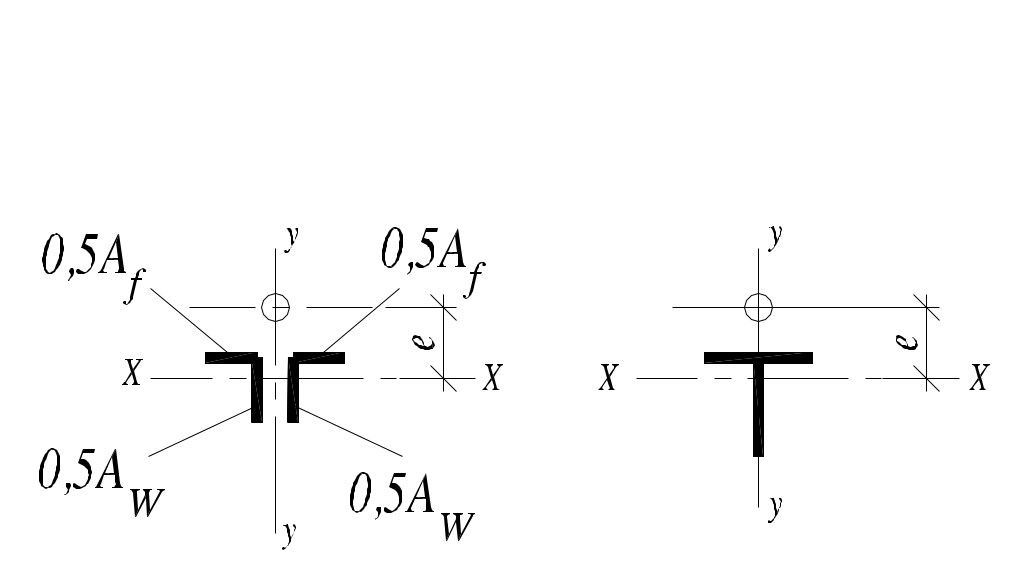	0,5	1,45+0,04m	1,65	1,45+0,04m		1,65
	1,0	1,8+0,12m	2,4	1,8+0,12m		2,4
	1,5	2,0+0,25m+0,1	—	—		—
	2,0	3,0+0,25m+0,1	—	—		—

---

В формуле φ_е – коэффициент устойчивости при сжатии с изгибом определяется для сплошностенчатых стержней в зависимости от условной гибкости и приведенного относительного эксцентриситетаm_ef (табл. 8.2), определяемого по формулеm_ef= ηm,

где η – коэффициент влияния формы сечения, определяемый по табл. 5.7 (предварительно для таврового сечения принимается η = 1,8);

m= e/ρ_x = eA/W_c– относительный эксцентриситет;

ρ_x= W_c/A – ядровое расстояние; W_c= I_x/z₀ – момент сопротивления сечения для наиболее сжатого волокна; z₀ ≈ 0,3h–расстояние от центра тяжести до наиболее сжатого волокна для таврового сечения; h– высота сечения.

При предварительном подборе сечения для поясов принимается гибкость λ = 60 – 90.

Задаемся гибкостью λ_х=l_x/i_х= 60.

Определяем отвечающие этой гибкости и расчетной длине стержня l_x:

– радиус инерции

i_x,тр= l_x/λ_x= 300 / 60 = 5 см;

– требуемую высоту сечения

h= i_x/α₁ = 5 / 0,3 ≈ 17 см (принимаем h= 18 см),

где α₁ ≈ 0,3 для таврового сечения из двух равнополочных уголков;

– ядровое расстояние

_x= W_c/A= (I_x/A)/z₀ = i²_x/z₀ = (0,3h)² / (0,3h)= 0,3h= 0,3 ∙ 18 = 5,4 см;

– приведенный эксцентриситет

m_ef = ηe/ρ_x = 1,8 ∙ 2,86 / 5,4 = 0,95;

– условную гибкость

.

По условной гибкости и приведенному эксцентриситету m_ef принимаем φ_е = 0,543.

Требуемая площадь сечения пояса

A_тр= N/(φ_еR_yγ_c) = 1300 / (0,543 ∙ 24 ∙ 0,95) = 105 см²_.

По A_тр и i_х,трпо сортаменту принимаем сечение из двух равнополочных уголков ∟

---

200×200×12 / ГОСТ 8510-86, имеющих характеристики:

А = 2 ∙ 47,1 = 94,2 см²; I_x = 2 ∙ 1822,78 = 3645,36 см⁴; i_х = 6,22 см;z_о = 5,37 см.

Определяем:

– момент сопротивления сечения для наиболее сжатого волокна

W_c= I_x/z_о = 3645,56 / 5,37 = 678,88 см³_;

– ядровое расстояние

ρ_x= W_c/А = 678,88 / 94,2 = 7,2 см;

– относительный эксцентриситет

m= e/ρ_x = 2,86 / 7,2 = 0,4;

– гибкость

λ_х= l_x/i_х = 300 / 6,22 = 48,2;

– условную гибкость



– по табл. 5.7 при A_f/A_w = 1 и = 1,64 вычисляем

η = 1,8 + 0,12m= 1,8 + 0,12 ∙ 0,4 = 1,85;

– приведенный эксцентриситет

m_ef= ηm= 1,85 ∙ 0,4 = 0,74.

По = 1,64 и m_ef= 0,74 определяем φ_е= 0,640.

Производим проверку пояса в плоскости действия момента:



Недонапряжение



Проверяем устойчивость пояса фермы из плоскости действия момента, для чего определяем:

– радиус инерции таврового сечения

см;

– момент инерции

I_y = i_y²A= 8,7² ∙ 94,2 = 7130 см⁴;

– гибкость

λ_у= l_у/i_у= 300 / 8,7 = 34,5.

Так как гибкость стержня λ_у = 34,5 < λ_х = 48,2 (жесткость ЕI_y > EI_x), проверка устойчивости пояса из плоскости действия момента не требуется.

При ЕI_y< ЕI_x проверка устойчивости сжато-изогнутого пояса из плоскости действия момента производится по формуле



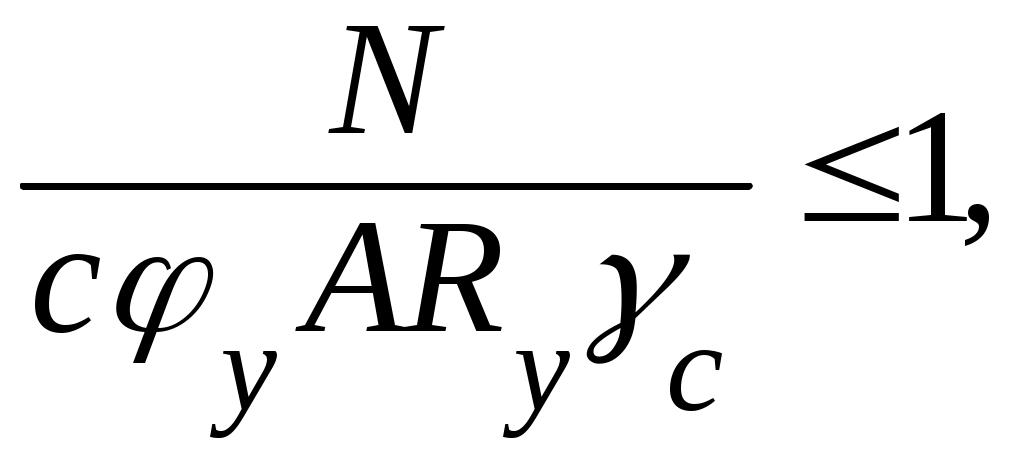
где φ_y– коэффициент устойчивости при центральном сжатии относительно оси y-y, принимается по условной гибкости

---

(см. табл. 3.11);

с – коэффициент, учитывающий изгибно-крутильную форму потери ус-

тойчивости и зависящий от относительного эксцентриситета и формы сечения, принимается по [6, п. 5.31].

При подборе сечения внецентренно-сжатых или сжато-изгибаемых элементов можно было воспользоваться наиболее простым, но менее точным способом определения требуемой площади сечения – методом последовательных приближений. Поскольку осевое усилие N играет определяющую роль, предварительно (с некоторым запасом) принимается сечение из расчета на усилие N как центрально-сжатого элемента, а затем оно проверяется с учетом действующего момента как внецентренно-сжатый элемент.
Пример 5.3. Подобрать сечение стержней растянутого нижнего пояса стропильной фермы по максимальному расчетному усилию в середине пролетаN_max = 1300 кН и минимальному расчетному усилению в крайней панели

N_min = 450 кН. Расчетная длина стержня в плоскости фермы l_x = 6 м. Материал конструкции – сталь С245; R_y = 24 кН/см² – расчетное сопротивление стали, коэффициент условий работы γ_с= 0,95.

Несущую способность элементов, выполненных из стали с нормативным сопротивлением R_yn ≤ 440 МПа и имеющих развитую площадку текучести, проверяют, исходя из условия развития пластических деформаций, по формуле



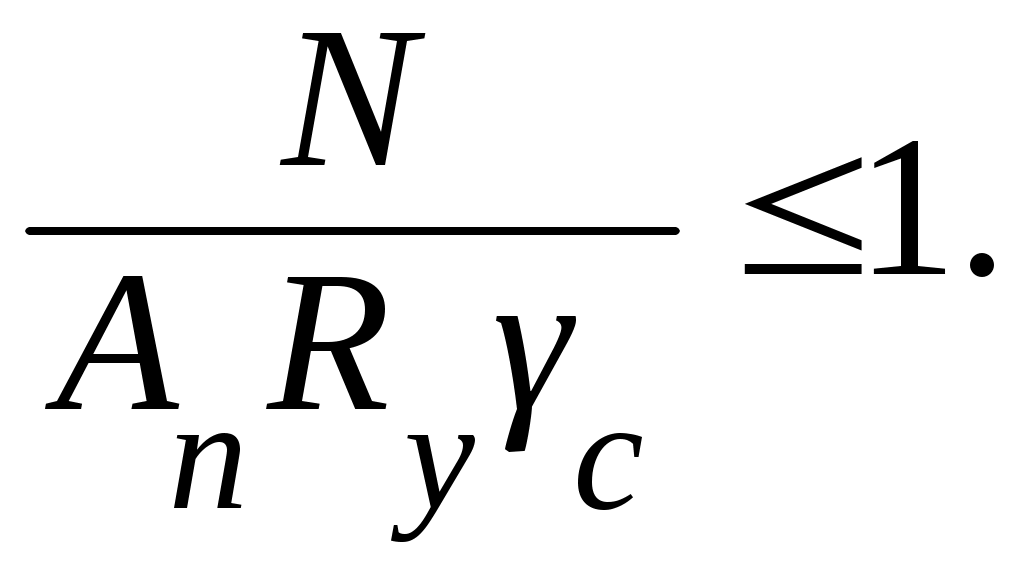
Для элементов, выполненных из сталей, не имеющих площадки текучести (условный предел текучести σ₀₂ > 440 МПа), а также, если эксплуатация конструкций возможна и после развития пластической деформации, проверка несущей способности производится по формуле



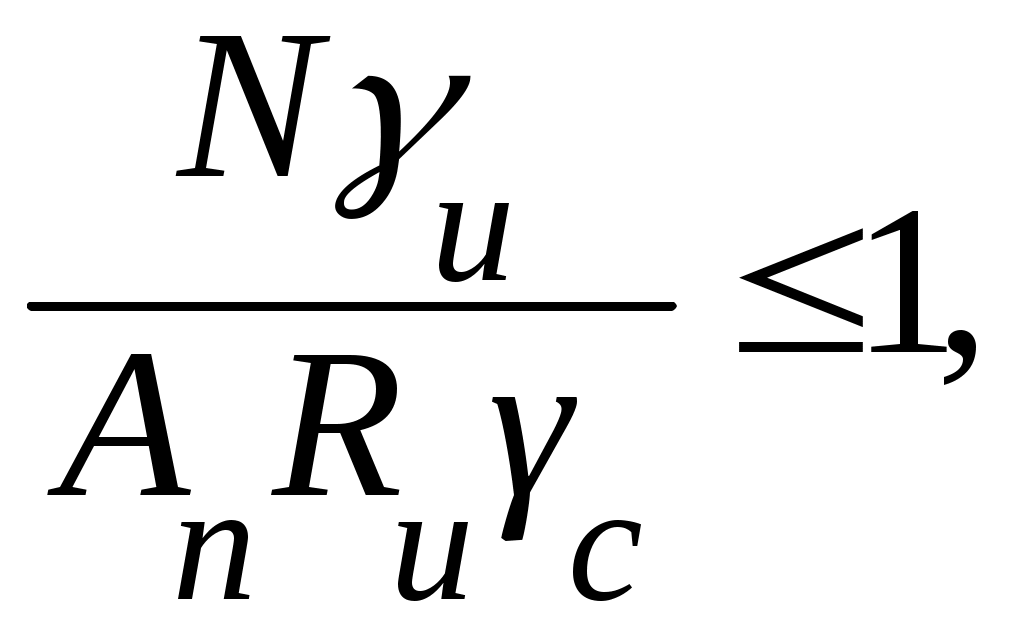
где R_u – расчетное сопротивление стали, определенное по временному сопротивлению (см. табл. 2.3); γ_u = 1,3 – коэффициент надежности при расчете по временному сопротивлению; A_п– площадь сечения нетто с учетом возможных ослаблений отверстиями под болты или заклепки; для сварных конструкций

---

A_п= А_вr.

Определяем требуемую площадь сечения нижнего пояса по максимальному усилию:

A_тр= N_max/(R_yγ_c) = 1300 / (24 ∙ 0,95) = 57,02 см².

Принимаем сечение из двух неравнополочных уголков, составленных узкими полками, ∟160×100×12, имеющих площадь сечения А = 30,04 ∙ 2 =

= 60,08 см² > A_тр = 57,02 см²; радиус инерции стержня в плоскости фермы i_x = 2,18 см; z_о= 2,36 см.

Проверяем растянутый пояса на прочность:



Проверяем гибкость в вертикальной плоскости (см. табл. 5.3):

λ_х= l_x/i_х= 600 / 2,18 = 275 < λ_и = 400.

Определяем площадь сечения по минимальному усилию

A_тр = N_min/(R_yγ_c) = 450 / (24 ∙ 0,95) = 19,74 см².

Принимаем сечение их двух неравнополочных уголков ∟100×63×7, составленных узкими полками, имеющих площадь сечения А = 11,09 ∙ 2 =

= 22,18 см² > A_тр = 19,74 см²; радиус инерцииi_x = 1,37 см; z_о = 1,46 см.

Проверяем гибкость в вертикальной плоскости:

λ_х=l_x/i_х= 600 / 1,37 = 438 > λ_и= 400.

Нижний пояс по гибкости не проходит. Принимаем сечение их двух равнополочных уголков ∟90×90×7, имеющих площадь сечения

А = 12,28 ∙ 2 = 24,56 см² > A_тр = 19,74 см²; радиус инерции i_x = 2,77 см; z_о = 2,47 см.

Гибкость в вертикальной плоскости

λ_х=l_x/i_х= 600 / 2,77 = 217 < λ_и= 400.

Проверяем пояса на прочность:



Сечение удовлетворяет условиям прочности и предельной гибкости.

Пример 5.4. Подобрать сечение сжатого среднего раскоса фермы по расчетному усилию N= – 75 кН. Расчетные длины раскоса: из плоскости фермы l_y = l= 4300 мм; в плоскости фермы l_x = 0,8l= 0,8 ∙ 4300 = 3440 мм. Материал конструкций – сталь С245.

Сечение средних малонагруженных элементов решетки фермы, как правило, подбирается по предельной гибкости λ_и.

В соответствии с табл. 5.2 для сжатого раскоса λ_и = 210 – 60.

Предварительно принимаем коэффициент  =

---