Файл: Учебнометодическое пособие по дисциплине физика часть 1 Физические основы механики. Электричество. Электромагнетизм. Для студентов 1 курса.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 527
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- + 3 нКл/м. Построить графики функций f1(r) иf2(r) для случаев:
I)r1 ; 2)R1 ≤ r ≤ R2 ; 3) г> R2
Вычислить разность потенциалов ∆φ между точками r1=4 см и r2= 9 см.
132* . Заряд 2,5.10-8 Кл равномерно распределен по всему объему однородного сферического диэлектрика ( ε= 5) радиусом R= 4,0 ом.
Построить графики функций f1(r) иf2(r) для случаев:
I) r ≤R ; г) r≥ R .
Вычислить разность потенциалов ∆φ между точками r1=2см и r2=9 см.
133*. Два бесконечно длинных цилиндрических проводника, оси которых совпадают, имеют радиусы R1=5см и R2 = 15 см. Цилиндры заряжены равномерно разноименно с линейной плотностью 2,5.10-9 Кл/м, причем заряд цилиндра меньшего радиуса отрицателен. Все пространство между цилиндрическими поверхностями заполнено однородным диэлектриком ( ε= 3,0).
Построить графики функций f1(r) иf2(r) для случаев:
I) г1 ; 2) R1 ≤r ≤ R2; 3) г>R2.
Вычислить разность потенциалов ∆φмежду точками r = 2 см иr= 14 см.
134*. Точечный заряд q = 1,6.10-9 Кл находится в центре шара радиусомR= 0,04 м из однородного изотропного диэлектрика. Его диэлектрическая проницаемость равна 2,5.
Построить графики функцийf1(r) иf2(r) для случаев:
I) r≤R; 2) r ≥ R.
Вычислить разность потенциалов ∆φ между точкамиr1 = 2 см и г2= 8 см.
135*. Сферическая поверхность радиусом R1 = 30 мм имеет равномерно распределенный заряд –5.10-8 Кл. На второй сферической поверхности радиусом R2 = 40мм равномерно распределен такой же по величине, но положительный заряд. Центры сферических поверхностей совпадают. Все пространство между сферическими поверхностями заполнено однородным диэлектриком ( ε= 5).
Построить графики функцийf1(r) иf2(r) для случаев:
I) r1 ; 2) R1 ≤r≤ R2 ; 3) г >R2.
Вычислить разность потенциалов ∆φмежду точками r1= 20мм и r2= 60 мм.
136*. Между двумя бесконечно длинными, коаксиальными и разноименно заряженными цилиндрическими поверхностями малых радиусов R1= 4 см и R2= 10 см находится слой диэлектрика ( ε = 3), прилегающего к цилиндрической поверхности меньшего радиуса R1 . Внешний радиус слоя диэлектрика R0 = 7 см. Линейная плотность заряда поверхности радиусом R1 составляет +3 нКл/м, внешней поверхности составляет -3 нКл/м.
Построить графики функций f1(r) иf2(r) для случаев:
1)r12) R1 ≤ r ≤R2; 3) r >R2.
Вычислить разность потенциалов ∆φ между точками r1 = 4 см и r2= 9 см.
137*. Заряд q =-5.10-7Кл равномерно распределен по всему объему однородного сферического диэлектрика ( ε = 3) радиусом R = 5,0 см.
Построить графики функцийf1(r) иf2(r) для случаев:
I) г ≤ R ; 2) г ≥R.
Вычислить разность потенциалов ∆φмежду точками r1=1cм и r2=8 см.
138*. Два бесконечно длинных цилиндрических проводника, оси которых совпадают, имеют радиусы R1= 6 см и R2 = 18 см. Цилиндры заряжены равномерно и разноименно с линейной плотностью 5.10-8 Кл/м, причем заряд цилиндра меньшего радиуса положителен. Все пространство между цилиндрическими поверхностями заполнено однородным диэлектриком ( ε = 5,0).
Построить графики функций f1(r) и f2(r) для случаев;
I) r1 ; 2) R1≤ r ≤ R2 ; 3) г>R2 .
Вычислить разность потенциалов ∆φ между точками r1= 3 см иr2= 15 см.
139*. Точечный заряд q =-2,1.10-8 Кл находится в центре шара радиусомR= 0,08м из однородного изотропного диэлектрика. Его диэлектрическая проницаемость равна 1,5.
Построить графики функцийf1(r) иf2(r) для случаев:
I) r ≤R1 ; 2)r ≥R2 .
Вычислить разность потенциалов ∆φ между точками r1= 1,5 см и r2 = 7 cм.
140*. Сферический проводник радиусом R1= 10 мм окружен примыкающим к нему слоем однородного диэлектрика с наружным радиусом R2 = 30 мм и диэлектрической проницаемостью ε= 1,5. На поверхности проводника равномерно распределен заряд q=1,8.10-8 Кл. Построить графики функций f1(r) иf2(r) для случаев:
I) r1;2) R1 ≤r ≤ R2 ; 3)r>R2.
Вычислить разность потенциалов ∆φ между точками r1 = 8мм и г2 = 40мм.
141. Определить проводимость и удельную тепловую мощность тока в проводнике с концентрацией электроновn=8.1028м-3и средней дрейфовой скоростью u= 2,8.10-2см/с, если разность потенциалов ∆φ двух точек однородного электрического поля в проводнике, отстоящих на l = 2.2 мм друг от друга, составила 1,4.10-4 В.
142. При равномерном нарастании плотности тока от нулевого значения в течение 5 с в проводнике сопротивлением 3 Ом и сечением 0,6 мм2 выделилось 7,5 Дж теплоты. Определить ток в конце последней секунды.
143. Сила тока в проводнике меняется со временем по законуI = 10sin50πtА. Найти заряд, протекающий через поперечное сечение проводника за время, равное 1/6 периода.
144. Вычислить количество теплоты, выделяемое в проводнике длиной l=10ми поперечным сечением S= 2 мм2 за первые 3 с, если его проводимость σ = 107Ом-1.м-1, а плотность тока в нем менялась от нулевого значения по закону j = 1,5.102t½мА/мм2.
145. Электрическое сопротивлениеR некоторого участка проводника длиной l = 0,6 м и сечениемS =1,5 мм2 составило 1,12 Ом. Определить тепловую удельную мощность, выделяемую на участке с напряженностью электрического поля Е = 0,56 В/м. Предполагая поле однородным, вычислить количество теплоты, выделяемое в проводнике за 15 с.
146. Количество теплотыQ, выделившееся за 4,4 с, при постоянной плотности тока в проводнике сечениемS =4мм2 длиной l=16 м, составило 20,8 Дж. Определить заряд q, прошедший через проводник за это время, и тангенциальную составляющую напряженности электрического поля, если его проводимостьσравна 5,7.106 Ом-1 см-1.
147. Средняя дрейфовая скорость электронов проводимости uпод действием электрического поля E = 0,36 В/м в металле с концентрацией носителей заряда n =1,25.1028 м-3 составила 10-3 м/с. Вычислить количество теплоты, выделяемое в объеме V = 16 см3 в промежутке времени между 3 и 5 секундами.
148. При равномерном нарастании тока в проводнике от нулевого значения за 0,5 с через его поперечное сечение S = 10 мм2 прошел заряд q= 17 Кл. Определить среднюю дрейфовую скорость электронов при достигнутой максимальной плотности тока, еслиихконцентрация составила 8,5.1028м-3.
149. Определить число электронов, проходящих в секунду через единицу площади поперечного сечения железной проволоки длиной l= 10 м и при напряжении на ее концах U=6 В. Удельное сопротивление железа ρ =9,8.10-6 Ом.см.
150. При равномерном нарастании тока от нуля до некоторого значения за 0,2 с в проводнике сопротивлениемR= 6 Ом выделилось Q = 8 Дж теплоты. Определить заряд, прошедший через полное сечение проводника.
151*. Бесконечный прямолинейный провод на некотором участке образует петлю в виде равностороннего треугольника, вершина которого находится на самой прямой, а его основание длиной 10 см параллельно ей. Найти магнитную индукцию в центре петли, если по проводу протекает ток силой 30 А.
152*. Проводник, по которому течет ток силой 3,2 А, представляет собой две полубесконечные параллельные прямые, замкнутые дугой радиусом 0,4 м, лежащей вне прямых, но в обшей плоскости. Найти величину магнитной индукции в центре кривизны дуги.
153*. Найти напряженность магнитного поля в центре кругового витка радиусом 9 см, помещенного в квадратную рамку со стороной 18 см так, чтоих плоскости совпадают, а направления токов в них силой 20 А противоположны.
154*. По бесконечно длинному проводу, изогнутому под прямым углом, протекает ток силой 50 А. Найти магнитную индукцию поля в центре кривизны изгиба провода по дуге радиусом 32 см.
155*. Найти напряженность магнитного поля в центре дуги радиусом 0,2 м, замыкающей два параллельных полубесконечных проводника, если лежат в плоскости, перпендикулярной плоскости дуги, а сила тока в цепи равна 14 А
156*. Проводник длинойl =1,4 м, по которому течет ток I=2,6 А, равномерно вращается в однородном магнитном поле (B= 0,1 Тл) вокруг оси, проходящей через один из его концов и параллельной вектору В. Период вращения Т = 0,2 с. Найти работу, совершенную за времяt= 40 с.
157*. Рамка, содержащаяN= 1500 витков площадьюS= 150 см2, равномерно вращается с частотой n = 960 об/мин в магнитном поле напряженностью Н= 105 А/м. Ось вращения лежит в плоскости рамки и перпендикулярна линиям напряженности. Определить максимальную ЭДС индукции, возникающую в рамке.
158*. Проволочный виток радиусом r= 14 см и сопротивлением R= 0,01 Ом находится в однородном магнитном поле (В = 0,2 Тл ). Плоскость витка составляет уголφ= 60° с линиями индукции. Какой заряд протечет по витку при выключении магнитного поля?
159*. Рамка площадью S= 220 см2 равномерно вращается с частотой n=10 с-1 относительно оси, лежащей в плоскости рамки и перпендикулярной линиям индукции однородного магнитного поля (В=0,12 Тл). Определить среднее значение ЭДС индукции за время, в течение которого магнитный поток, пронизывающий рамку, изменится от нуля до максимального значения.
160*. Тонкий проводник с сопротивлением R= 14 Ом и длиной l = 1,5 м согнут в виде квадрата и концы его замкнуты. Квадрат помещен в однородное магнитное поле (В= 0,1 Тл) так, что его плоскость перпендикулярна линиям поля. Определить заряд Q, который протечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЧЕТУ
Механика
r = 10t2ex + 16tey+8ez. Запишите выражение для вектора скорости v(t), найдите угол между вектором скорости и осью х.
Дайте определение ускорения а материальной точки.
Что характеризует тангенциальная (а) составляющая ускорения материальной точки? Нормальная составляющая (аn) ускорения материальной точки? Как выражаются их модули? Чему равен модуль полного ускорения а? Запишите соответствующие формулы.
Что собой представляет траектория движения частицы, если : а = 0 и аn =0; a = constиan = 0; a = f(t) иan = 0; a = 0 иan = const; a = 0 иan 0
Вектор скорости материальной точки меняется со временем по закону
v = 20tex + 16ey. Найдите ускорение а материальной точки.
Что называется абсолютно твердым телом? Какое движение абсолютно твердого тела называется вращательным?
Что называется угловой скоростью? Как определяется направление угловой скорости? Каким соотношением связаны между собой линейнаяvи угловая скорости? Как они взаимно направлены? Каким является вращение, если = const?
Что называется периодом вращения Т ? Как он связан с угловой скоростью ? Что называется частотой вращения n? Как она связана с периодом Т и с угловой скоростью ?
Тело вращается с угловой скоростью = 12,56 рад/с. Найти число оборотов N, которое совершит тело за время t = 5 минут.
Колесо при равномерном вращении совершает N = 5 оборотов за время t1=1c На какой угол повернется радиус колеса за время t2 = 0,5 с ?
Что называется угловым ускорением ? Как направлен вектор углового ускорения ? Каким является вращение,если вектор сонаправлен вектору , направлен противоположно ему? Как связаны между собой модули тангенциальной составляющей ускорения а и углового ускорения ?
Напишите формулы, связывающие линейные величины ( длина пути S, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а, нормальное ускорение аn ) и угловые величины ( угол поворота , угловая скорость , угловое ускорение ).
Что такое сила? Дайте определение. Каковы возможные результаты действия силы на тело? Как определяются сила тяготения, сила тяжести, вес, сила упругости, сила трения скольжения? Напишите соответствующие формулы.
Что такое масса тела? Зависит ли масса тела от его расположения (широты места, высоты над поверхностью Земли)? Зависит ли масса тела от скорости его движения? Если да, то в каком случае? Что называется импульсом материальной точки? Напишите соответствующую формулу.
В каких системах отсчета справедливы законы Ньютона? Сформулируйте первый закон Ньютона. Является ли он следствием второго закона Ньютона? Ответ обоснуйте.
Приведите две формулировки второго закона Ньютона, напишите соответствующие формулы.
С каким ускорением надо поднимать груз на нити, чтобы сила натяжения нити была в 1,5 раза больше силы тяжести груза?
Что называется механической системой? Какие системы называются замкнутыми? Какие силы являются внешними? Какие силы являются внутренними? Сформулируйте и напишите закон сохранения импульса. В каких системах этот закон выполняется? Может ли быть ситуация, при которой импульс в целом не сохраняется, но сохраняется одна из его проекций? Если да, то в каком случае?
Пуля массой m1= 0,02 кг, летящая горизонтально со скоростью v1 = 600 м/с, попадает в брусок массой m2 = 1кг, стоящий на гладкой горизонтальной поверхности, и, пробив его, вылетает со скоростью v2 = 400 м/с. Определить, с какой скоростью будет двигаться брусок.
Электростатика, постоянный ток и электромагнетизм
ПРИМЕРЫ ТЕСТОВЫХ ЗАДАНИЙ ДЛЯ ПОДГОТОВКИ К ТЕСТИРОВАНИЮ
Механика:
ТЗ№1.На рисунке представлена траектория материальной точки. Вектор перемещения м.т. из 1 в 2 это вектор….
Ответ: С
Т
З №2. Если l– пройденный телом путь между двумя точками, а 
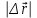- модуль соответствующего перемещения, то
А)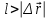
;
В)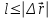
;
С)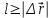
;
Д)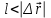
.
ТЗ№3. Число степеней свободы системы, состоящей из трех материальных точек, жестко связанных между собой невесомыми нерастяжимыми стержнями (трехатомная молекула), равно: i = ….
Ответ: 6
ТЗ№4. Векторное произведение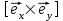
равно
А)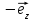
;
В)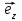
;
С) 0;
Д) 1.
ТЗ№5 Камень брошен под углом к горизонту у поверхности Земли со скоростью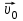
. Нормальное ускорение в верхней точке траектории равно:
А) gtg;
В) gsin;
С) gcos;
Д) g.
ТЗ№6. Мальчик равномерно вращается на карусели радиусом R = 2 м с угловой скоростью = 0,5 рад/с. За время t = 4 с длина пути, пройденного мальчиком, равна: L = … м.
Ответ: 4
ТЗ№7. Санки массой m остаются в покое на горизонтальной поверхности под действием силы F, направленной вверх под углом к горизонту. Коэффициент трения равен . Модуль силы трения, действующей на тело, равен:
A
) mg; B) Fcos ; C) (mg - Fsin); D) (mg + Fsin).
ТЗ№8. Момент импульса системы сохраняется:
А) только если система замкнута;
В) только когда векторная сумма всех внешних сил, действующих на систему, равна нулю;
С) лишь при выполнении условия
I)r
Вычислить разность потенциалов ∆φ между точками r1=4 см и r2= 9 см.
132* . Заряд 2,5.10-8 Кл равномерно распределен по всему объему однородного сферического диэлектрика ( ε= 5) радиусом R= 4,0 ом.
Построить графики функций f1(r) иf2(r) для случаев:
I) r ≤R ; г) r≥ R .
Вычислить разность потенциалов ∆φ между точками r1=2см и r2=9 см.
133*. Два бесконечно длинных цилиндрических проводника, оси которых совпадают, имеют радиусы R1=5см и R2 = 15 см. Цилиндры заряжены равномерно разноименно с линейной плотностью 2,5.10-9 Кл/м, причем заряд цилиндра меньшего радиуса отрицателен. Все пространство между цилиндрическими поверхностями заполнено однородным диэлектриком ( ε= 3,0).
Построить графики функций f1(r) иf2(r) для случаев:
I) г
Вычислить разность потенциалов ∆φмежду точками r = 2 см иr= 14 см.
134*. Точечный заряд q = 1,6.10-9 Кл находится в центре шара радиусомR= 0,04 м из однородного изотропного диэлектрика. Его диэлектрическая проницаемость равна 2,5.
Построить графики функцийf1(r) иf2(r) для случаев:
I) r≤R; 2) r ≥ R.
Вычислить разность потенциалов ∆φ между точкамиr1 = 2 см и г2= 8 см.
135*. Сферическая поверхность радиусом R1 = 30 мм имеет равномерно распределенный заряд –5.10-8 Кл. На второй сферической поверхности радиусом R2 = 40мм равномерно распределен такой же по величине, но положительный заряд. Центры сферических поверхностей совпадают. Все пространство между сферическими поверхностями заполнено однородным диэлектриком ( ε= 5).
Построить графики функцийf1(r) иf2(r) для случаев:
I) r
Вычислить разность потенциалов ∆φмежду точками r1= 20мм и r2= 60 мм.
136*. Между двумя бесконечно длинными, коаксиальными и разноименно заряженными цилиндрическими поверхностями малых радиусов R1= 4 см и R2= 10 см находится слой диэлектрика ( ε = 3), прилегающего к цилиндрической поверхности меньшего радиуса R1 . Внешний радиус слоя диэлектрика R0 = 7 см. Линейная плотность заряда поверхности радиусом R1 составляет +3 нКл/м, внешней поверхности составляет -3 нКл/м.
Построить графики функций f1(r) иf2(r) для случаев:
1)r
Вычислить разность потенциалов ∆φ между точками r1 = 4 см и r2= 9 см.
137*. Заряд q =-5.10-7Кл равномерно распределен по всему объему однородного сферического диэлектрика ( ε = 3) радиусом R = 5,0 см.
Построить графики функцийf1(r) иf2(r) для случаев:
I) г ≤ R ; 2) г ≥R.
Вычислить разность потенциалов ∆φмежду точками r1=1cм и r2=8 см.
138*. Два бесконечно длинных цилиндрических проводника, оси которых совпадают, имеют радиусы R1= 6 см и R2 = 18 см. Цилиндры заряжены равномерно и разноименно с линейной плотностью 5.10-8 Кл/м, причем заряд цилиндра меньшего радиуса положителен. Все пространство между цилиндрическими поверхностями заполнено однородным диэлектриком ( ε = 5,0).
Построить графики функций f1(r) и f2(r) для случаев;
I) r
Вычислить разность потенциалов ∆φ между точками r1= 3 см иr2= 15 см.
139*. Точечный заряд q =-2,1.10-8 Кл находится в центре шара радиусомR= 0,08м из однородного изотропного диэлектрика. Его диэлектрическая проницаемость равна 1,5.
Построить графики функцийf1(r) иf2(r) для случаев:
I) r ≤R1 ; 2)r ≥R2 .
Вычислить разность потенциалов ∆φ между точками r1= 1,5 см и r2 = 7 cм.
140*. Сферический проводник радиусом R1= 10 мм окружен примыкающим к нему слоем однородного диэлектрика с наружным радиусом R2 = 30 мм и диэлектрической проницаемостью ε= 1,5. На поверхности проводника равномерно распределен заряд q=1,8.10-8 Кл. Построить графики функций f1(r) иf2(r) для случаев:
I) r
Вычислить разность потенциалов ∆φ между точками r1 = 8мм и г2 = 40мм.
141. Определить проводимость и удельную тепловую мощность тока в проводнике с концентрацией электроновn=8.1028м-3и средней дрейфовой скоростью u= 2,8.10-2см/с, если разность потенциалов ∆φ двух точек однородного электрического поля в проводнике, отстоящих на l = 2.2 мм друг от друга, составила 1,4.10-4 В.
142. При равномерном нарастании плотности тока от нулевого значения в течение 5 с в проводнике сопротивлением 3 Ом и сечением 0,6 мм2 выделилось 7,5 Дж теплоты. Определить ток в конце последней секунды.
143. Сила тока в проводнике меняется со временем по законуI = 10sin50πtА. Найти заряд, протекающий через поперечное сечение проводника за время, равное 1/6 периода.
144. Вычислить количество теплоты, выделяемое в проводнике длиной l=10ми поперечным сечением S= 2 мм2 за первые 3 с, если его проводимость σ = 107Ом-1.м-1, а плотность тока в нем менялась от нулевого значения по закону j = 1,5.102t½мА/мм2.
145. Электрическое сопротивлениеR некоторого участка проводника длиной l = 0,6 м и сечениемS =1,5 мм2 составило 1,12 Ом. Определить тепловую удельную мощность, выделяемую на участке с напряженностью электрического поля Е = 0,56 В/м. Предполагая поле однородным, вычислить количество теплоты, выделяемое в проводнике за 15 с.
146. Количество теплотыQ, выделившееся за 4,4 с, при постоянной плотности тока в проводнике сечениемS =4мм2 длиной l=16 м, составило 20,8 Дж. Определить заряд q, прошедший через проводник за это время, и тангенциальную составляющую напряженности электрического поля, если его проводимостьσравна 5,7.106 Ом-1 см-1.
147. Средняя дрейфовая скорость электронов проводимости uпод действием электрического поля E = 0,36 В/м в металле с концентрацией носителей заряда n =1,25.1028 м-3 составила 10-3 м/с. Вычислить количество теплоты, выделяемое в объеме V = 16 см3 в промежутке времени между 3 и 5 секундами.
148. При равномерном нарастании тока в проводнике от нулевого значения за 0,5 с через его поперечное сечение S = 10 мм2 прошел заряд q= 17 Кл. Определить среднюю дрейфовую скорость электронов при достигнутой максимальной плотности тока, еслиихконцентрация составила 8,5.1028м-3.
149. Определить число электронов, проходящих в секунду через единицу площади поперечного сечения железной проволоки длиной l= 10 м и при напряжении на ее концах U=6 В. Удельное сопротивление железа ρ =9,8.10-6 Ом.см.
150. При равномерном нарастании тока от нуля до некоторого значения за 0,2 с в проводнике сопротивлениемR= 6 Ом выделилось Q = 8 Дж теплоты. Определить заряд, прошедший через полное сечение проводника.
151*. Бесконечный прямолинейный провод на некотором участке образует петлю в виде равностороннего треугольника, вершина которого находится на самой прямой, а его основание длиной 10 см параллельно ей. Найти магнитную индукцию в центре петли, если по проводу протекает ток силой 30 А.
152*. Проводник, по которому течет ток силой 3,2 А, представляет собой две полубесконечные параллельные прямые, замкнутые дугой радиусом 0,4 м, лежащей вне прямых, но в обшей плоскости. Найти величину магнитной индукции в центре кривизны дуги.
153*. Найти напряженность магнитного поля в центре кругового витка радиусом 9 см, помещенного в квадратную рамку со стороной 18 см так, чтоих плоскости совпадают, а направления токов в них силой 20 А противоположны.
154*. По бесконечно длинному проводу, изогнутому под прямым углом, протекает ток силой 50 А. Найти магнитную индукцию поля в центре кривизны изгиба провода по дуге радиусом 32 см.
155*. Найти напряженность магнитного поля в центре дуги радиусом 0,2 м, замыкающей два параллельных полубесконечных проводника, если лежат в плоскости, перпендикулярной плоскости дуги, а сила тока в цепи равна 14 А
156*. Проводник длинойl =1,4 м, по которому течет ток I=2,6 А, равномерно вращается в однородном магнитном поле (B= 0,1 Тл) вокруг оси, проходящей через один из его концов и параллельной вектору В. Период вращения Т = 0,2 с. Найти работу, совершенную за времяt= 40 с.
157*. Рамка, содержащаяN= 1500 витков площадьюS= 150 см2, равномерно вращается с частотой n = 960 об/мин в магнитном поле напряженностью Н= 105 А/м. Ось вращения лежит в плоскости рамки и перпендикулярна линиям напряженности. Определить максимальную ЭДС индукции, возникающую в рамке.
158*. Проволочный виток радиусом r= 14 см и сопротивлением R= 0,01 Ом находится в однородном магнитном поле (В = 0,2 Тл ). Плоскость витка составляет уголφ= 60° с линиями индукции. Какой заряд протечет по витку при выключении магнитного поля?
159*. Рамка площадью S= 220 см2 равномерно вращается с частотой n=10 с-1 относительно оси, лежащей в плоскости рамки и перпендикулярной линиям индукции однородного магнитного поля (В=0,12 Тл). Определить среднее значение ЭДС индукции за время, в течение которого магнитный поток, пронизывающий рамку, изменится от нуля до максимального значения.
160*. Тонкий проводник с сопротивлением R= 14 Ом и длиной l = 1,5 м согнут в виде квадрата и концы его замкнуты. Квадрат помещен в однородное магнитное поле (В= 0,1 Тл) так, что его плоскость перпендикулярна линиям поля. Определить заряд Q, который протечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЧЕТУ
Механика
-
Что необходимо задать для определения системы отсчета, относительно которой рассматривается движение тела? -
В какой системе отсчета траектория движения мухи, ползущей по спице велосипедного колеса прямолинейна: в системе отсчета, связанной с Землей, с осью колеса, со спицей колеса? -
Какое тело можно назвать материальной точкой? Приведите примеры. -
Что такое траектория движения материальной точки? -
Может ли длина траектории зависеть от выбора системы отсчета? -
Что такое радиус-вектор r, и как с его помощью описать траекторию движения материальной точки? -
Приведите соотношение, связывающее радиус-вектор r с координатами x, y, zматериальной точки. -
Что такое путь? Что такое перемещение? -
Материальная точка описала при своем движении половину окружности радиусом R = 5м. Чему равен путь Sи модуль вектора перемещения r точки? -
Материальная точка движется из пункта А с координатами (5,0) в пункт В с координатами (-3,0). Чему равна проекция перемещения на ось ох? -
Дайте определение вектора скорости vматериальной точки. -
Приведите соотношение, связывающее вектор скоростиvс его проекциями на координатные оси vx, vy, vz. -
Радиус-вектор материальной точки меняется со временем по закону:1 2 3 4 5 6
r = 10t2ex + 16tey+8ez. Запишите выражение для вектора скорости v(t), найдите угол между вектором скорости и осью х.
Дайте определение ускорения а материальной точки.
Что характеризует тангенциальная (а) составляющая ускорения материальной точки? Нормальная составляющая (аn) ускорения материальной точки? Как выражаются их модули? Чему равен модуль полного ускорения а? Запишите соответствующие формулы.
Что собой представляет траектория движения частицы, если : а = 0 и аn =0; a = constиan = 0; a = f(t) иan = 0; a = 0 иan = const; a = 0 иan 0
Вектор скорости материальной точки меняется со временем по закону
v = 20tex + 16ey. Найдите ускорение а материальной точки.
Что называется абсолютно твердым телом? Какое движение абсолютно твердого тела называется вращательным?
Что называется угловой скоростью? Как определяется направление угловой скорости? Каким соотношением связаны между собой линейнаяvи угловая скорости? Как они взаимно направлены? Каким является вращение, если = const?
Что называется периодом вращения Т ? Как он связан с угловой скоростью ? Что называется частотой вращения n? Как она связана с периодом Т и с угловой скоростью ?
Тело вращается с угловой скоростью = 12,56 рад/с. Найти число оборотов N, которое совершит тело за время t = 5 минут.
Колесо при равномерном вращении совершает N = 5 оборотов за время t1=1c На какой угол повернется радиус колеса за время t2 = 0,5 с ?
Что называется угловым ускорением ? Как направлен вектор углового ускорения ? Каким является вращение,если вектор сонаправлен вектору , направлен противоположно ему? Как связаны между собой модули тангенциальной составляющей ускорения а и углового ускорения ?
Напишите формулы, связывающие линейные величины ( длина пути S, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а, нормальное ускорение аn ) и угловые величины ( угол поворота , угловая скорость , угловое ускорение ).
Что такое сила? Дайте определение. Каковы возможные результаты действия силы на тело? Как определяются сила тяготения, сила тяжести, вес, сила упругости, сила трения скольжения? Напишите соответствующие формулы.
Что такое масса тела? Зависит ли масса тела от его расположения (широты места, высоты над поверхностью Земли)? Зависит ли масса тела от скорости его движения? Если да, то в каком случае? Что называется импульсом материальной точки? Напишите соответствующую формулу.
В каких системах отсчета справедливы законы Ньютона? Сформулируйте первый закон Ньютона. Является ли он следствием второго закона Ньютона? Ответ обоснуйте.
Приведите две формулировки второго закона Ньютона, напишите соответствующие формулы.
С каким ускорением надо поднимать груз на нити, чтобы сила натяжения нити была в 1,5 раза больше силы тяжести груза?
Что называется механической системой? Какие системы называются замкнутыми? Какие силы являются внешними? Какие силы являются внутренними? Сформулируйте и напишите закон сохранения импульса. В каких системах этот закон выполняется? Может ли быть ситуация, при которой импульс в целом не сохраняется, но сохраняется одна из его проекций? Если да, то в каком случае?
Пуля массой m1= 0,02 кг, летящая горизонтально со скоростью v1 = 600 м/с, попадает в брусок массой m2 = 1кг, стоящий на гладкой горизонтальной поверхности, и, пробив его, вылетает со скоростью v2 = 400 м/с. Определить, с какой скоростью будет двигаться брусок.
-
Напишите формулу для определения работыпостоянной силы. Работа является скалярной величиной или векторной? Может ли быть работа силы отрицательной? Может ли быть работа силы равной нулю? Ответ обоснуйте. Можно ли вычислить работу силы графически? Если можно,то как?
Ящик массойm= 20 кг равномерно перемещают по горизонтальной поверхности на расстояние S=30 м с помощью веревки, образующей угол =30 с горизонтом. Определить работу, затраченную на перемещение ящика, если коэффициент трения k=0,1. -
Напишите формулу для определения работы переменной силы. Получите выражение для работы силы упругости. Определить работу, совершаемую при растяжении пружины на L=0,2 м, если при растяжении этой пружины на l=0,4 м необходимо приложить силу F=8 Н. -
Дайте определения и напишите соответствующие формулы для всех известных вам видов механической энергии.
Работой каких сил обусловлено изменение кинетической энергии?
Работой каких сил обусловлено изменение потенциальной энергии?
Какие силы называются консервативными? Чему равна работа консервативных сил по замкнутому пути? Приведите примеры консервативных сил.
Какова связь между консервативной силой и изменением потенциальной энергии тела? Напишите соответствующую формулу. -
Чему равна убыль потенциальной энергии частицы, перемещающейся в стационарном поле сил? Напищите соответствующую формулу.
Потенциальная энергия частицы имеет вид U = 5xyz. Напишите выражение, определяющее силу, действующую на эту частицу. -
Как определяется полная механическая энергия тела?
При каком условии полная механическая энергия тела сохраняется? Действие каких сил приводит к ее изменению? -
Как определяется полная механическая энергия системы материальных точек? Напишите соответствующее соотношение. Какие системы материальных точек называются консервативными? Какие системы называются диссипативными?
Для каких систем выполняется закон сохранения механической энергии? Сформулируйте его. -
Действие каких сил может изменить полную механическую энергию системы материальных точек?
Сохраняется ли полная механическая энергия системы материальных точек, если : а) в системе отсутствует действие сил трения и сопротивления, и система не является замкнутой?
б) система замкнута , и в ней действуют силы трения?
в) система замкнута , и в ней отсутствует действие сил трения и сопротивления?
г) система не замкнута, но на нее действуют только консервативные силы?
Является ли необходимым условием выполнения закона сохранения механической энергии наличие замкнутости системы материальных точек? -
Что называется моментом силы относительно неподвижной точки? Напишите соответствующую формулу. Сделайте поясняющий чертеж. Укажите на нем направление момента силы. Обоснуйте указанное направление. -
Что называется моментом силы относительно неподвижной оси? Напишите соответствующую формулу. Сделайте поясняющий чертеж. Укажите на нем направление момента силы. Обоснуйте указанное направление. -
Диск радиусомR вращается против часовой стрелки вокруг неподвижной оси, проходящей перпендикулярно плоскости диска через его центр. Чему равен и как направлен момент силы F, действующей по касательной к ободу диска? Сделайте поясняющий чертеж. -
Что называется моментом инерции тела относительно оси вращения? Что характеризует момент инерции тела? Зависит ли момент инерции тела от положения оси вращения? Как определить момент инерции материальной точки относительно оси вращения? Напишите соответствующую формулу.
Напишите формулу для определения момента инерции системы , состоящей из n материальных точек относительно оси вращения. -
Напишите формулу для определения момента инерции тела относительно оси вращения в случае непрерывного распределения масс.
Выведите формулу для момента инерции тонкого стержня массой m и длинойlотносительно оси проходящей: а) через центр стержня перпендикулярно его длине; б) через конец стержня перпендикулярно его длине. -
Как определяется кинетическая энергия тела, вращающегося вокруг неподвижной оси?
Шар массой m = 0,25 кг катится по горизонтальной поверхности без проскальзывания со скоростью v = 4 м/с. Определить его полную кинетическую энергию. -
Напишите уравнение динамики вращательного движения твердого тела. Приведите вывод этого уравнения.
Маховик в виде сплошного диска, момент инерции которого I= 1,5 кг/м2, вращаясь при торможении равнозамедленно, за время t = 1 мин уменьшил частоту своего вращения с n0 = 240 об/мин до n1 = 120 об/мин. Найти угловое ускорение маховика и момент М силы торможения. -
Что называется моментом импульса материальной точки? твердого тела? Как определить направление момента импульса. Напишите формулу, связывающую изменение момента импульса с моментом силы.
Электростатика, постоянный ток и электромагнетизм
-
Что понимается под дискретностью электрического заряда? Какие частицы обладают элементарным зарядом? В чем заключается закон сохранения заряда? Приведите примеры проявления этого закона. -
Напишите закон Кулона. Поясните смысл всех входящих в него величин.
Можно ли применить закон Кулона для определения силы взаимодействия между равномерно заряженным стержнем и точечным зарядом, расположенным на продолжении оси стержня? Ответ обоснуйте. -
Что называется напряженностью Е электростатического поля? Как определяется направление вектора напряженности Е? Зависит ли величина напряженности Е в данной точке поля от величины пробного заряда qпр, помещенного в эту точку? Чему равна напряженность поля Е, создаваемого точечным зарядомq на расстоянии r от него? Пользуясь принципом суперпозиции, найдите в поле двух точечных зарядов +Qи +2Q, находящихся на расстоянии r друг от друга, точку, где напряженность поля равна нулю. -
Напишите формулу, определяющую поток вектора напряженности электростатического поля ФЕ через площадку dS. Поясните смысл всех входящих в формулу величин. Сделайте поясняющий чертеж. Напишите формулу, определяющую поток вектора напряженности электростатического поля ФЕ через произвольную замкнутую поверхность S. Может ли поток ФЕ быть положительным, отрицательным, равным нулю? Приведите соответствующие примеры. -
Напишите формулу, выражающую теорему Гаусса для электростатического поля в вакууме. Примените эту теорему для определения напряженности поля Е равномерно заряженной сферической поверхности, равномерно заряженного бесконечного цилиндра (нити). -
Напишите формулу, определяющую потенциальную энергию Wточечного заряда q0в поле точечного заряда q. В каком случае энергия Wположительна, в каком отрицательна? -
Что такое потенциал данной точки электростатического поля? Дайте определение и напишите соответствующее выражение. Напишите формулу, определяющую потенциал поля точечного заряда. Что такое разность потенциалов? Напишите соответствующую формулу. -
Какова связь между напряженностью и потенциалом? Напишите соответствующее выражение. Найти разность потенциалов между двумя точками, лежащими на расстояниях х1 и х2 от равномерно заряженной с поверхностной плотностью заряда бесконечной плоскости. -
Что называется силой тока? Что называется плотностью тока? Напишите соответствующие формулы. Определить плотность тока, если за tс через проводник сечениемSм2 прошло Nэлектронов. Назовите условия возникновения и существования электрического тока. -
Что называется электродвижущей силой? Какие силы являются сторонними? -
Напишите закон Ома для неоднородного участка цепи. Поясните смысл всех входящих в него величин. Получите частные случаи этого закона: закон Ома для однородного участка цепи, закон Ома для замкнутой цепи.
Выведите закон Ома в дифференциальной форме. -
Напишите закон Джоуля-Ленца. Выведите дифференциальную форму этого закона.
К концам проводника приложено напряжение U = 10 В. Какой заряд должен пройти по проводнику, чтобы в нем выделилось Q = 1000 Дж тепла? -
Чему равен и как направлен магнитный момент рамки с токомpm? Как определяется вращающий момент сил М, действующий на рамку с током в магнитном поле. -
Что такое вектор индукции магнитного поля В? Как можно определить величину вектора индукции магнитного поля В? Что такое линии магнитной индукции? Как определяется их направление? Чем они отличаются от линий напряженности электростатического поля? Нарисуйте и покажите, как направлены линии магнитной индукции поля прямого тока. -
Напишите закон Био-Савара-Лапласа, поясните смысл всех входящих в него величин. Пользуясь этим законом, выведите формулу для определения индукции магнитного поля В : 1) прямого тока; 2) в центре кругового проводника с током. -
Напишите закон Ампера. Поясните смысл всех входящих в него величин. Как определяется направление силы Ампера? Сделайте поясняющий чертеж. -
Выведите формулу для определения силы взаимодействия двух бесконечных прямолинейных одинаковых токов противоположного направления. Сделайте поясняющий чертеж, указав на нем направления токов, вектора индукции В, силF12и F21, действующих на каждый из проводников. -
Напишите формулу, определяющую силу Лоренца. Как направлена сила , действующая на отрицательный электрический заряд, движущийся в магнитном поле? -
Как определяется поток вектора индукции магнитного поля Ф? Напишите соответствующую формулу. Сделайте поясняющий чертеж. -
В чем заключается явление электромагнитной индукции? Что является причиной возникновения э.д.с. в замкнутом проводящем контуре? Напишите закон Фарадея для электромагнитной индукции. Сформулируйте правило Ленца, проиллюстрировав его примером. Какова природа э.д.с. электромагнитной индукции?
ПРИМЕРЫ ТЕСТОВЫХ ЗАДАНИЙ ДЛЯ ПОДГОТОВКИ К ТЕСТИРОВАНИЮ
Механика:
ТЗ№1.На рисунке представлена траектория материальной точки. Вектор перемещения м.т. из 1 в 2 это вектор….
Ответ: С
Т
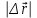З №2. Если l– пройденный телом путь между двумя точками, а - модуль соответствующего перемещения, тоА)
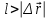;В)
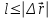;С)
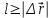;Д)
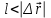.ТЗ№3. Число степеней свободы системы, состоящей из трех материальных точек, жестко связанных между собой невесомыми нерастяжимыми стержнями (трехатомная молекула), равно: i = ….
Ответ: 6
ТЗ№4. Векторное произведение
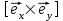равноА)
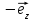;В)
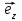;С) 0;
Д) 1.
ТЗ№5 Камень брошен под углом к горизонту у поверхности Земли со скоростью
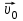. Нормальное ускорение в верхней точке траектории равно:А) gtg;
В) gsin;
С) gcos;
Д) g.
ТЗ№6. Мальчик равномерно вращается на карусели радиусом R = 2 м с угловой скоростью = 0,5 рад/с. За время t = 4 с длина пути, пройденного мальчиком, равна: L = … м.
Ответ: 4
ТЗ№7. Санки массой m остаются в покое на горизонтальной поверхности под действием силы F, направленной вверх под углом к горизонту. Коэффициент трения равен . Модуль силы трения, действующей на тело, равен:
A
) mg; B) Fcos ; C) (mg - Fsin); D) (mg + Fsin).ТЗ№8. Момент импульса системы сохраняется:
А) только если система замкнута;
В) только когда векторная сумма всех внешних сил, действующих на систему, равна нулю;
С) лишь при выполнении условия