Файл: Учебнометодическое пособие по дисциплине физика часть 1 Физические основы механики. Электричество. Электромагнетизм. Для студентов 1 курса.docx

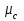найдем по определенным выше значениям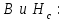



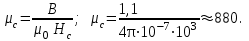
Теперь можно найти :

,



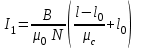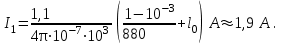
Плотность энергии магнитного поля определяется известной формулой



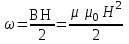
Индукция поля в сердечнике и зазоре согласно соотношению (2) одинакова и определена была выше 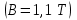для значения 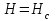по графику . Напряженность в зазоре найдем по из формул (3)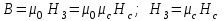



Найдем :



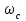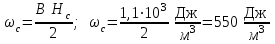
Найдем


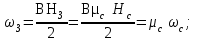
КОНТРОЛЬНАЯ РАБОТА № 1

Студент должен решить шесть задач того варианта, номер которо­го совпадает с последней цифрой его шифра (номера студенческого билета).

Вариант	Задачи
0 1 2 3 4 5 6 7 8 9	110* 101* 102* 103* 104* 105* 106* 107* 108* 109*	120 111* 112* 113* 114* 115* 116* 117* 118* 119*	130* 121* 122* 123* 124* 125* 126* 127* 128* 129*	140* 131* 132* 133* 134* 135* 136* 137* 138* 139*	150 141 142 143 144 145 146 147 148 149	160* 151* 152* 153* 154* 155* 156* 157* 158* 159*

ПРИМЕЧАНИЯ:1. Решения задач, отмеченных звездочкой, должны сопро­вождаться чертежами (рисунками),графиками.

---

2.В задачах 131*-140* нужно:

а) Найти значения векторов напряженности электрического поля Е и электрического смещения D как функцию расстоянияr , от­считываемого от центра или оси симметрии, для случаев, указываемых в каждой конкретной задаче.

б) ГрафикиE=f₁(r) и D=f₂(r) расположить на одном чер­теже, как показано в примере 5.

в). Вычислить разность потенциалов Δφ между двумя точками, указанными в каждой конкретной задаче.

101*.Два одинаковых груза массамиm₁= m₂ = 0,5 кг связаны нитью, перекинутой через блок, укрепленный на конце стола (рис.1). Радиус блока R=0,2 м, масса блокаm=1кг. Найти угловое ускорение блока, если коэффициент трения груза m₂ о стол µ=0,2. Блок считать сплошным диском.




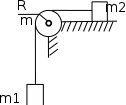
Рис.1 Рис.2
102*. Блок в виде сплошного диска массой m=0,5кг укреплен на конце стола (рис.1). Грузы m₁=2 кг и m₂ =3 кг соединены нитью, перекинутой через блок.Радиус блока R=0,2 м. Коэффициент трения груза m₂ о стол µ=0,2. Найти угловое ускорение блока.

103*. На полый тонкостенный цилиндр (рис.2) намотана тонкая нить, свободный конец которой прикреплен к потолку. Найти ускорение, с которым цилиндр опускается под действием силы тяжести.

104*. Тонкая нить намотана на полый тонкостенный цилиндр массой m=1кг. Свободный конец нити прикреплен к потолку (рис.2). Найти натяжение нити при опускании цилиндра под действием силы тяжести.

105*. Найти угловое ускорение диска массой m=1кг и радиусом R=0,3м (рис.3), на который намотан шнур с привязанным грузом массой m₁=0,5 кг. Найти натяжение шнура.




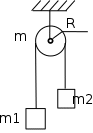
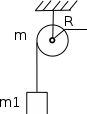
Рис.3 Рис.4
106*. Груз массой m₁=3 кг привязан к нити, намотанной на барабан (рис.3). Найти радиус барабана и натяжение нити, если момент инерции барабана J=3,0 кг٠м², а груз опускается с ускорением а=2,0 м/с².

107*. Два груза m₁=1 кг и m₂ =0,5 кг связаны легким шнуром, перекинутым через блок (рис.4). Блок радиусом R=10 см вращается с угловым ускорением β =20 рад/с² . Найти массу блока, если она равномерно распределена по его ободу.

108*. Два груза m₁=2 кг и m₂ =1,5 кг связаны легким шнуром, перекинутым через блок (рис.4) радиусом R=25 см и массой m=4 кг. Найти ускорения грузов, угловое ускорение блока и натяжение нитей.

---

109*. К вращающемуся диску массой m=30 кг и радиусом R=10 см прижата тормозная колодка с силой F=12Н (рис.5). Найти время, за которое диск остановится, если угловая скорость его вращения ω₀ = 15рад/с, а коэффициент трения µ = 0,4.




Рис.5
110*. К вращающемуся диску массой m=40 кг и диаметром D = 30 см прижимается тормозная колодка (рис.5) с силой F=20Н, в результате чего диск останавливается в течение времениt = 15 с. Коэффициент трения µ = 0,4. Найти начальную частоту ν₀ вращения диска.

111^*. Платформа в виде горизонтально расположенного диска может вращаться вокруг вертикальной оси, проходящей через центр платфор­мы. На платформе находится человек, которого в условии задачи мож­но рассматривать как материальную точку. Расходом энергиина пре­одоление сил трения пренебречь. Человек массой 60 кг стоит на краю платформы массой 120 кг, делающей 3,0 об/мин. Сколько оборотов в минуту будет делать плат­форма, если человек перейдет на середину между краем и центром платформы?

112^*. Начало условия смотрите в задаче 111. Человек массой 60 кг стоитна краю платформы массой 100 кг, делающей 5 об/мин. Сколь­ко оборотов в минуту будет делать платформа, если человек перейдет в центр платформы?

I13*. Начало условия смотрите в задаче 111. Человек массой 70 кг стоит на неподвижной платформе массой 100 кг. Человек обходит платформу вдоль ее края и останавливается в той точке платформы, от которой начал обход. На какой угол (в градусах) повернулась платформа?

I14^*. Начало условия смотрите в задаче 111. Человек массой 60 кг стоит на краю неподвижной платформы. С какой скоростью (относи­тельно платформы) должен пойти человек вдоль края платформы, что­бы она начала вращаться со скоростью, соответствующей 3,0 об/мин? Масса платформы 120 кг, ее радиус 2,0 м.

I15*. Начало условия смотрите в задаче 111. Человек массой 75 кг стоит на краю платформы, делающей 3 об/мин. С какой скоростью должен идти человек вдоль края платформы, чтобы его скорость отно­сительно Земли стала равной нулю? Масса платформы 100 кг, ее ра­диус 1,6 м.

I16*. Человек стоит на скамье Жуковского и ловит рукой мяч мас­сой 0,4 кг, летящий горизонтально со скоростью 20 м/с. Траектория мяча проходит на расстоянии 0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью начнет вращаться скамья с челове­ком, если суммарный момент инерции человека и скамьи равен 6 кг^.м² ?

I17^*. Человек, стоя на скамье Жуковского, ловит рукой мяч, ле­тящий горизонтально со скоростью 16 м/с на расстоянии 0,7 м от вертикальной оси вращенияскамьи

---

. Найти массу мяча, если суммарный момент инерции скамьи с человеком равен 6 кг^.м² , а угловая скорость вращения скамьи равна I рад/с.

I18*. Начало условия смотрите в задаче 111. Человек сидит на неподвижной платформе и держит в руках над головой конец шнура, к другому концу которого привязан груз массой 2 кг. Найти период, с которым будет вращаться платформа с человеком, если человек приведет во вращение шнур с грузом, который, делая I оборот в секунду, будет описывать в горизонтальной плоскости окружность радиусом 2 м. Момент инерции платформы с человеком равен 10 кг^.м². Массой шнура и силами трения пренебречь.

I19*. Начало условия смотрите в задаче 111.Человек массой 60 кг стоит на краю платформы радиусом 2 м и массой 150 кг. Найти уг­ловую скорость, с которой будет вращаться платформа, если человек пойдет вдоль ее края со скоростью 1м/с относительно платформы. Момент инерции человека рассчитывать как для материальной точки.

120. В центр деревянного шара радиусом 7см, лежащего на столе, попадает пуля массой 10 г, летящая горизонтально со скоростью 350 м/с, и застревает в нем. Найти массу шара, если он после уда­ра покатится без скольжения с угловой скоростью 22 рад/с.

121*. Два одинаковых заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол α. Шарики погружаются в масло плотностью ρ=8^.10² кг/м⁸. Какова диэлектрическая проницаемость ε масла, если угол расхож­дения нитей при погружении шариков в масло остается неизменным? Плотность материалов шариков ρ=1,6^.10³ кг/м³.

122*. Тонкое полукольцо радиусом R=10 см несет равномер­но распределенный заряд с линейной плотностью τ=10^-6 Кл/м. В центре кривизны полукольца находится точечный заряд q = 2^.10^-10 Кл. Определить силу взаимодействия точечного заряда и заряженного по­лукольца.

123*. Заряд с линейной плотностью τ=3^.10^-6 Кл/м равномер­но распределен по тонкому полукольцу, в центре кривизны которого находится точечный заряд q = 5^.10^-11 Кл. Сила взаимодействия то­чечного заряда и заряженного полукольца равна 5^.10^-5 Н. Найти ра­диус полукольца.

124*. Точечный заряд q=3^.10^-11 Кл находится в центре кри­визны тонкого полукольца радиусом R= 5 см, равномерно заряжен­ного с линейной плотностьюτ. Сила взаимодействия точечного за­ряда и заряженного полукольца равна 6

---

^.10^-5 Н. Определить линейную плотность заряда полукольца τ.

125*. На тонком кольце равномерно распределен заряд с линей­ной плотностью зарядаτ= 20 нКл/см. Радиус кольца R= 5 см. На перпендикуляре к плоскости кольца, восставленномиз его середины, находится точечный заряд q = 40 нКл. Определить силу, действую­щую на точечный заряд со стороны заряженного кольца, если он уда­лен от центра кольца на:I) а₁= 10 см; 2) а₂= 2 м.

126*. Определить напряженность поля, создаваемого зарядом, равномерно распределенным по тонкому прямому стержню длиной l= 10 см, с линейной плотностью заряда τ = 100 нКл/м, в точке, ле­жащей на продолжении оси стержня на расстоянии a = 10 см от бли­жайшего конца. Определить также силу, действующую в этой точке на точечный заряд q =10 нКл.

127^*. Найти силу взаимодействия между тонкой бесконечной нитью с линейной плотностью зарядаτ₁= 0,278 нКл/м и тонким стержнем длиной l =17,1 см с линейной плотностью заряда τ₂= 0,4 нКл/м, еслиихоси взаимно перпендикулярны, а ближайший конец стержня, лежаще­го в радиальной плоскости, находится в 10 см от нити.

128^*. По тонкому кольцу радиусом R= 6 см равномерно рас­пределен заряд Q= 24 нКл. Какова напряженность поля в точке, находящейся на оси кольца на расстоянии a= 18 см от центра коль­ца? Найти также силу, действующую в этой точке на точечный зарядq= 0,5 нКл.

129^*. Одна четвертая часть тонкого кольца радиусомR= 10 см несет равномерно распределенный заряд с линейной плотностью τ=2^.10^-5 Кл/м. В центре кривизны кольца находится точечный заряд q=5^.10^-5 Кл. Определить силу взаимодействия точечного заряда и заряженной части кольца.

130*. Два полубесконечных, тонких равномерно заряженных стержня расположены перпендикулярно друг к другу так, что точка пересеченияих осей находится на расстоянии а = 8 см и b = 5 см от ближайших концов стержней. Найти силу, действующую на заряд q= 10 нКл, помещенный в точку пересечения осей стержней, по­лагая линейную плотность их зарядов одинаковой и равной τ=1,5 нКл/см.

131^* Между двумя бесконечно длинными, коаксиальными и разно­именно заряженными цилиндрическими поверхностями малых радиусов R₁ = 4 см и R₂ = 10 см находится слой диэлектрика ( ε = 3), при­легающего к цилиндрической поверхности большего радиуса R₂ . Мень­ший радиус диэлектрического слоя R₀ = 7 см. Линейная плотность заряда поверхности радиусом R₁ составляет -3 нКл/м, а внешней поверхности радиусом R₂

---