Файл: Учебнометодическое пособие по дисциплине физика часть 1 Физические основы механики. Электричество. Электромагнетизм. Для студентов 1 курса.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 522
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
П р и м е р 1.Уравнение движения материальной точки вдоль оси X в системе СИ имеет вид:
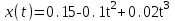
Определить значения скорости
 и ускорения аtв моменты времени
и ускорения аtв моменты времени 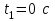 и
и 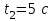 , а также среднюю скорость
, а также среднюю скорость 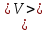 и среднее ускорение
и среднее ускорение 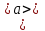 в первые пять секунд движения.
в первые пять секунд движения.Дано:
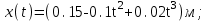
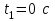 ;
; 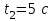
Найти:
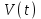 ;
; 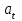 ;
; 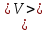 и
и 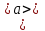 .
.Р е ш е н и е .Скорость является первой производной от координаты по времени
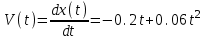 .
.Скорость в моменты времени
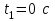 и
и 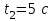 равна
равна 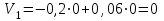 и
и 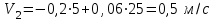
Ускорение является первой производной от скорости по времени. (Здесь идёт речь лишь о тангенциальном ускорении, так как движение прямолинейно
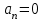 и а(t)
и а(t)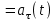 .
.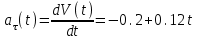 .
.Ускорение в моменты времени
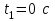 и
и 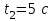 равно
равно 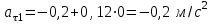 и
и 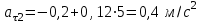
.
Средняя скорость может быть определена по формуле
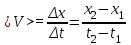
Значения
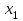 и
и 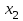 для моментов времени
для моментов времени  и
и  :
: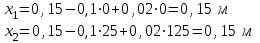
Средняя скорость в первые пять секунд движения равна
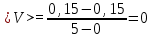
Среднее ускорение за первые пять секунд движения равно
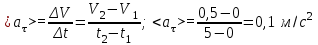 .
.П р и м е р 2. С вышки высотой
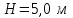 брошен камень (в условиях задачи принять камень за материальную точку) вверх под углом
брошен камень (в условиях задачи принять камень за материальную точку) вверх под углом 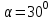 к горизонтальной плоскости со скоростью
к горизонтальной плоскости со скоростью 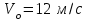 .
.-
Составить уравнение движения материальной точки с числовыми коэффициентами. -
Определить, на каком расстоянии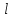 от подножья вышки камень упадёт на землю.
от подножья вышки камень упадёт на землю.
3. Определить для момента времени
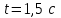 :
:3.1 Скорость
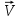 ;
;3.2. Тангенциальную
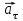 и нормальную
и нормальную 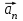 составляющие ускорения ;
составляющие ускорения ;-
Радиус кривизны траектории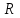 . Сопротивлением воздуха пренебречь.
. Сопротивлением воздуха пренебречь.
Дано:
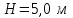 ;
; 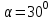 ;
; 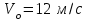 ;
; 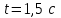 .
.Н
 айти:
айти: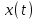 ;
; 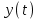 ;
; 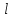
;
 ;
;  ;
;  ;
;  .
.Р
 е ш е н и е. 1. Для составления уравнений движения материальной точки выберем систему отсчета - прямоугольную систему координат XY (рис 1), начало отсчета которой поместим у подножья вышки; ось X направим горизонтально в сторону броска, а ось Y – вертикально вверх. Разложим сложное движение материальной точки на более простые вдоль выбранных осей X и Y : вдоль оси Х материальная точка имеет начальную скорость
е ш е н и е. 1. Для составления уравнений движения материальной точки выберем систему отсчета - прямоугольную систему координат XY (рис 1), начало отсчета которой поместим у подножья вышки; ось X направим горизонтально в сторону броска, а ось Y – вертикально вверх. Разложим сложное движение материальной точки на более простые вдоль выбранных осей X и Y : вдоль оси Х материальная точка имеет начальную скорость 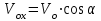 ; ускорение вдоль оси X отсутствует, так как единственная сила, сообщающая ускорение - сила притяжения Земли, направлена вдоль оси Y, и проекция её на ось X равна нулю; таким образом, движение вдоль оси X –равномерное с постоянной скоростью
; ускорение вдоль оси X отсутствует, так как единственная сила, сообщающая ускорение - сила притяжения Земли, направлена вдоль оси Y, и проекция её на ось X равна нулю; таким образом, движение вдоль оси X –равномерное с постоянной скоростью 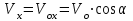 . Следовательно, движение вдоль оси описывается уравнением
. Следовательно, движение вдоль оси описывается уравнением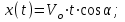 x(t) = 12tcos 30˚ = 10,4 t м . (1)
x(t) = 12tcos 30˚ = 10,4 t м . (1)Вдоль оси Y материальная точка имеет начальную скорость
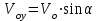 . Действующая вдоль этой оси сила притяжения Земли сообщает ускорение
. Действующая вдоль этой оси сила притяжения Земли сообщает ускорение 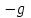 , таким образом, движение вдоль оси Y является равнопеременным, и координата движущейся вдоль оси Y точки определяется уравнением
, таким образом, движение вдоль оси Y является равнопеременным, и координата движущейся вдоль оси Y точки определяется уравнением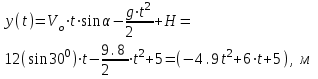 (2)
(2)Найденные уравнения движения
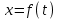 и
и 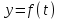 позволяют без особых затруднений решить остальные вопросы задачи.
позволяют без особых затруднений решить остальные вопросы задачи.2. В момент падения камня на землю координаты точки:
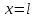 - искомое расстояние от подножья вышки до места падения, и y=0. Подставляя эти значения в уравнения (1) и (2) , получим:
- искомое расстояние от подножья вышки до места падения, и y=0. Подставляя эти значения в уравнения (1) и (2) , получим: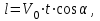 (1/)
(1/)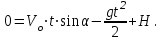 (2/)
(2/) Выразим из уравнения (1/)
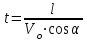
, подставим это значение в уравнение (2/):
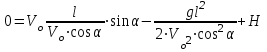 .
.Подставляя данные значения
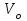 ,
,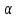 ,
,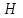 ,получим
,получим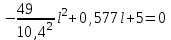
или
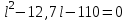
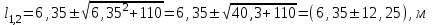
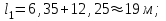
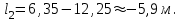
Второе решение
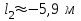 в условиях данной задачи не имеет смысла.
в условиях данной задачи не имеет смысла.-
Для момента времени определяем:
определяем:
-
Скорость в момент найдем уравнения составляющих скорости:
найдем уравнения составляющих скорости:
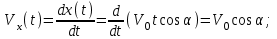
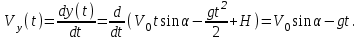
После подстановки числовых значений и вычислений получим значения составляющих для момента
 :
: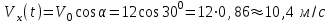
и
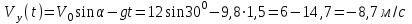
Величина же скорости (полной) в этот момент равна
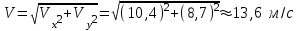
3.2. Тангенциальная
 (касательная) составляющая ускорения
(касательная) составляющая ускорения 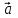 определяется по величине (рис. 2) как проекция полного ускорения на направление скорости (касательной к траектории движения):
определяется по величине (рис. 2) как проекция полного ускорения на направление скорости (касательной к траектории движения): 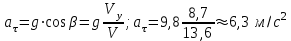

Аналогично определяется и величина нормальной
 составляющей ускорения:
составляющей ускорения: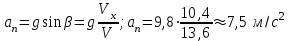
3.3. Значение радиуса
