Файл: Федеральное агентство по рыболовству Федеральное государственное бюджетное образовательное.docx

Коэффициенты передаточной функции определяются по формулам, исходя из таблиц интегральных площадей:









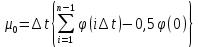
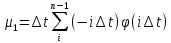
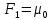
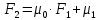
Таблица 1 – Расчет по методу Симаю основного канала регулирования.

i	t	Кривая разгона	Нормированная функция	Вспомогательная функция φ(t)	(-i*Δt)	φ(t)(-i*Δt)
0	0	0	0	1	0	0
1	60	0	0	1	-60	-60
2	180	3	0,01875	0,98125	-180	-176,625
3	240	6	0,0375	0,9625	-240	-231
4	300	10	0,0625	0,9375	-300	-281,25
5	360	15,7	0,098125	0,901875	-360	-324,675
6	420	22,4	0,14	0,86	-420	-361,2
7	480	31	0,19375	0,80625	-480	-387
8	540	38,5	0,240625	0,759375	-540	-410,0625
9	600	47,85	0,299063	0,7009375	-600	-420,5625
10	660	59,8	0,37375	0,62625	-660	-413,325
11	720	72	0,45	0,55	-720	-396
12	780	84,3	0,526875	0,473125	-780	-369,0375
13	840	96	0,6	0,4	-840	-336
14	900	107,85	0,674063	0,3259375	-900	-293,34375
15	960	118,5	0,740625	0,259375	-960	-249
16	1020	128	0,8	0,2	-1020	-204
17	1080	137,4	0,85875	0,14125	-1080	-152,55
18	1140	143	0,89375	0,10625	-1140	-121,125
19	1200	147,85	0,924063	0,0759375	-1200	-91,125
20	1260	151,9	0,949375	0,050625	-1260	-63,7875
21	1320	155	0,96875	0,03125	-1320	-41,25
22	1380	156	0,975	0,025	-1380	-34,5

---

Продолжение таблицы 1

23	1440	157	0,98125	0,01875	-1440	-27
24	1500	157,85	0,986563	0,0134375	-1500	-20,15625
25	1560	158,7	0,991875	0,008125	-1560	-12,675
26	1620	159,1	0,994375	0,005625	-1620	-9,1125
27	1680	160	1	0	-1680	0
28	1740	160	1	0	-1740	0
29	1800	160	1	0	-1800	0
			сумма	12,220625	сумма 1	-5486,3625
			момент 0	703,2375	момент 1	-329181,75
			F1	703,2375	F2	165361,2314

---

Передаточная функция по основному каналу аппроксимирована апериодическим звеном второго порядка с запаздыванием:



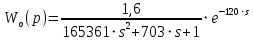
Аппроксимированная кривая разгона приведена на рисунке 5.



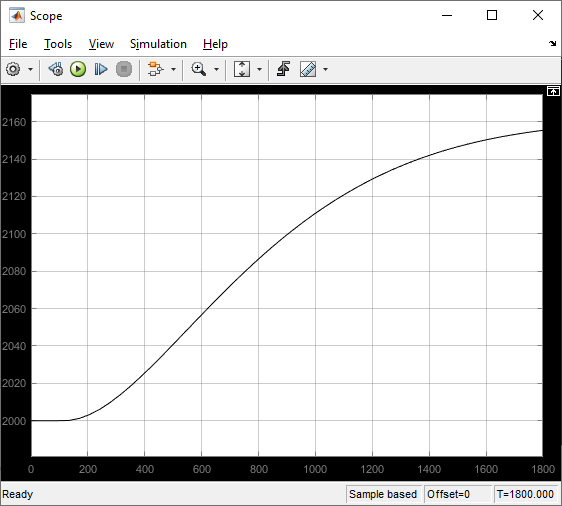
Рисунок 5 – Переходная функция объекта управления по каналу управления (моделирование)

Передаточная функция по возмущению аппроксимирована апериодическим звеном второго порядка с запаздыванием:



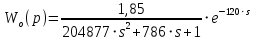
Аппроксимированная кривая разгона по вспомогательному каналу регулирования (Simulink) приведена на рисунке 6.



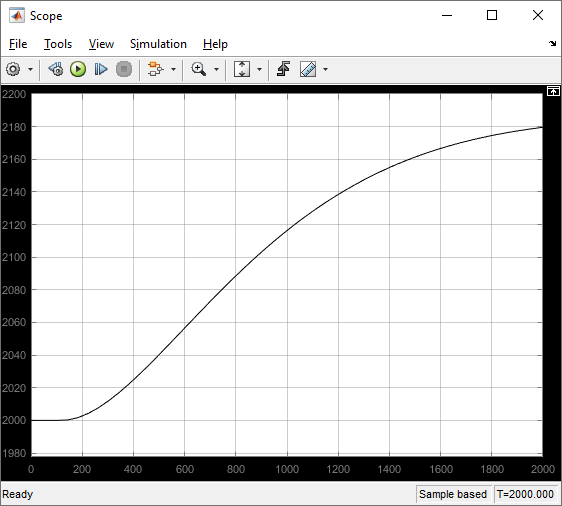
Рисунок 6 – Переходная функция объекта управления по каналу возмущения (моделирование)

При обработке кривой разгона по вспомогательному каналу получены следующие данные:

• 
  коэффициент передачи объекта 1,85 мм/м³/час;
  
• 
  транспортное запаздывание объекта – 120 секунд.
  

2.2.3 Частотные характеристик объекта управления

Частотные характеристики объекта по каналу управления приведены на рисунках 5, 6 и 7, по каналу возмущения приведены на рисунках 8, 9 и 10.



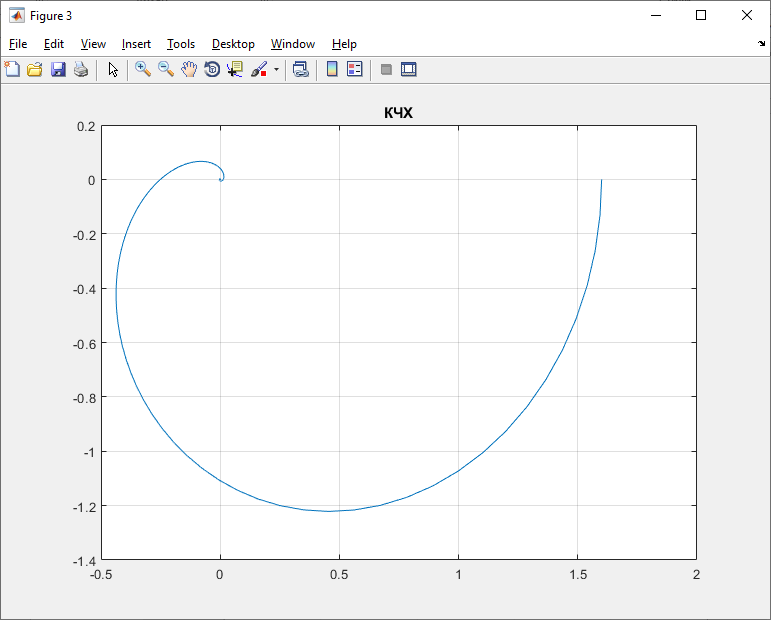
Рисунок 7 – Комплексно-частотная характеристика каналу управления



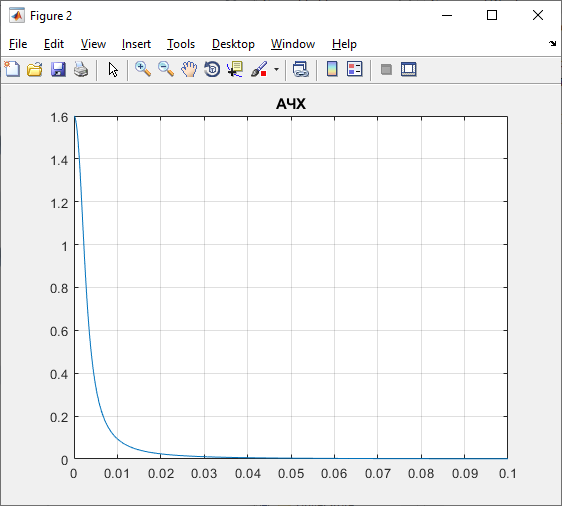
Рисунок 8 – Амплитудно-частотная характеристика по каналу управления (моделирование)



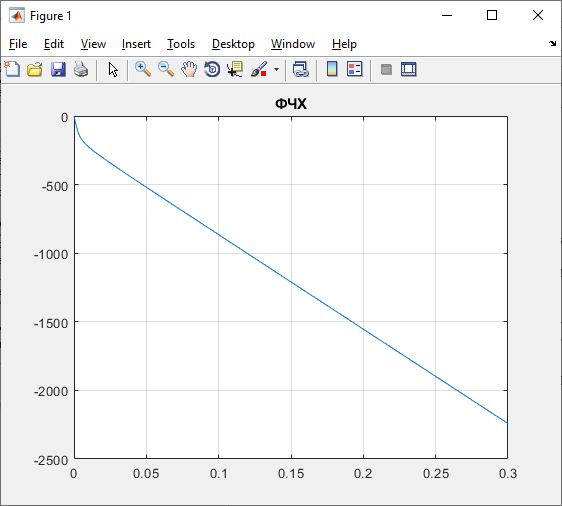
Рисунок 9 – Фазо-частотная характеристика по каналу управления (моделирование)



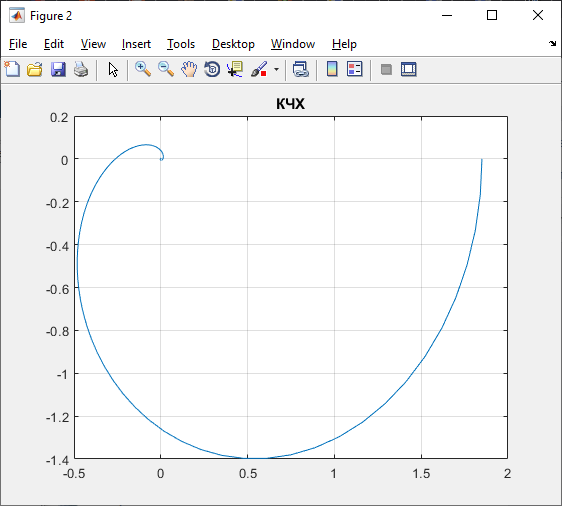
Рисунок 10 – Комплексно-частотная характеристика по каналу возмущения



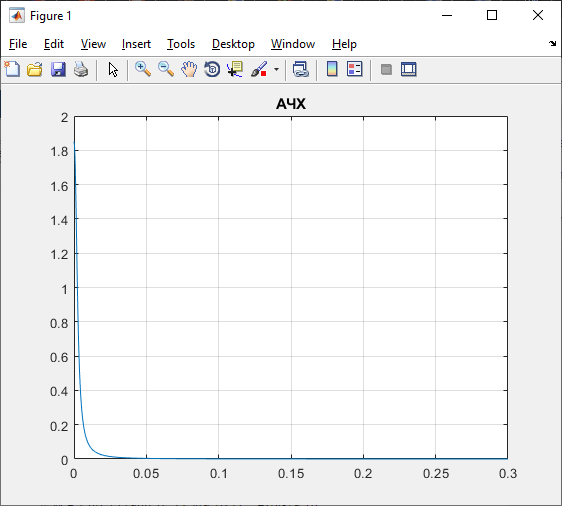
Рисунок 11 – Амплитудно-частотная характеристика по каналу возмущения



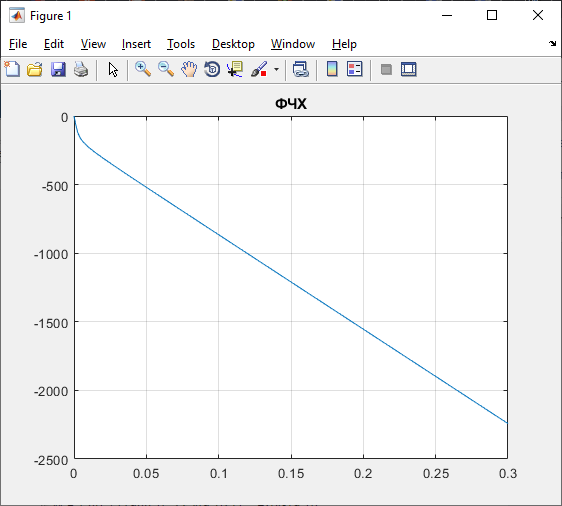
Рисунок 12 – Фазо-частотная характеристика по каналу возмущения

---

2.2.4 Расчет одноконтурной системы

Расчет параметров настроек регулятора одноконтурной системы автоматического регулирования произведем методом Циглера-Никольса. Для этого было проведено моделирование системы с ПИ-регулятором (рис. 11).

Расчет настроек регулятора одноконтурной системы проводится по каналу основной регулируемой величины. Для получения значений оптимальных настроек регулятора применяется метод РКЧХ. Расчет проводится для степени затухания ψ = 0.9, при значении степени колебательности m = 0.366. В одноконтурной системе используется ПИ-регулятор, что обеспечивает высокое качество регулирования без статической ошибки.

В соответствии с методом РКЧХ выражения для настроечных параметров ПИ-регулятора C₀ и C₁ имеют вид:

С₀ = ·(m²+1)·Im(W^*(m,)_об)

С₁ = m·Im(W^*(m,)_об) – Re(W^*(m,)_об),

где W*(m,) – инверсная расширенная комплексная частотная характеристика объекта управления W*(m,) = 1/W(m,)_об.

Инверсная РКЧХ и комплексные выражения для передаточной функции объекта получены с помощью программы Mathcad. Кривая равной степени колебательности показана на рисунке 12.



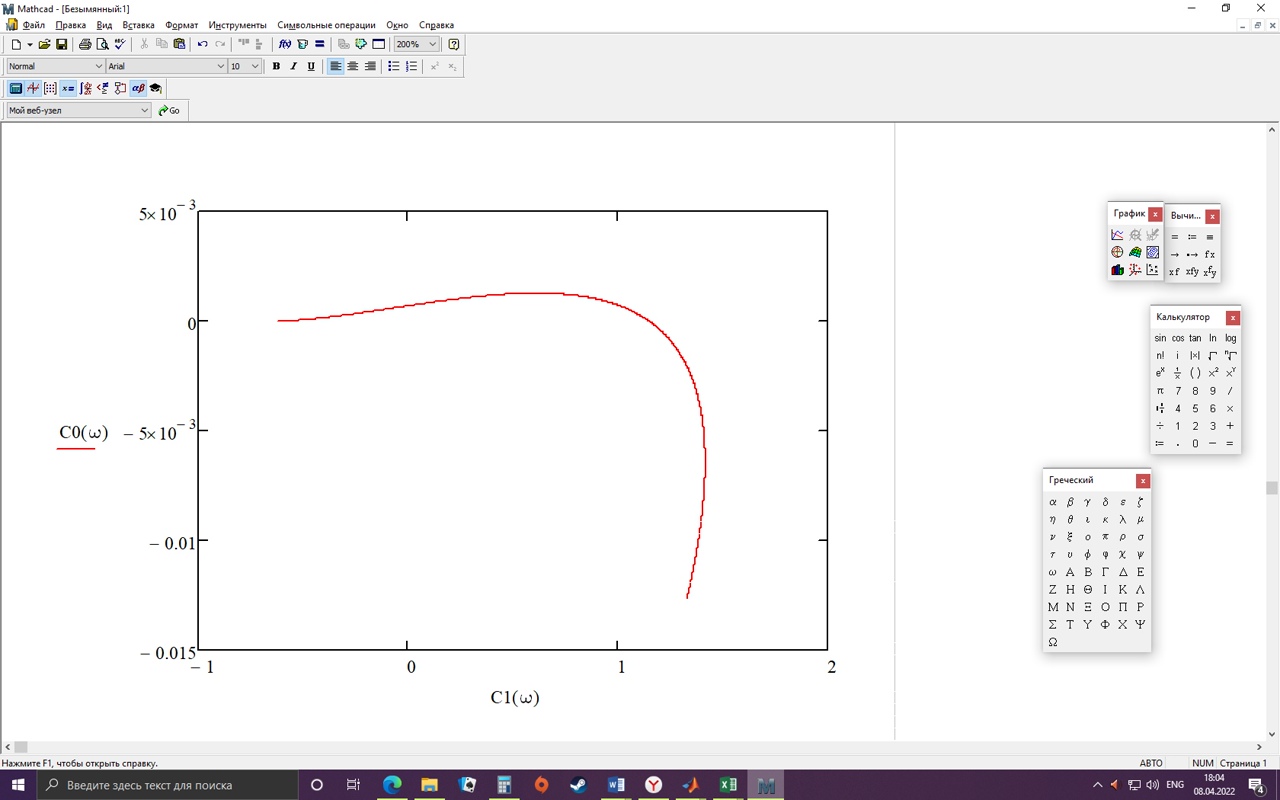
Рисунок 12. Кривая равной степени колебательности регулятора в одноконтурной системе



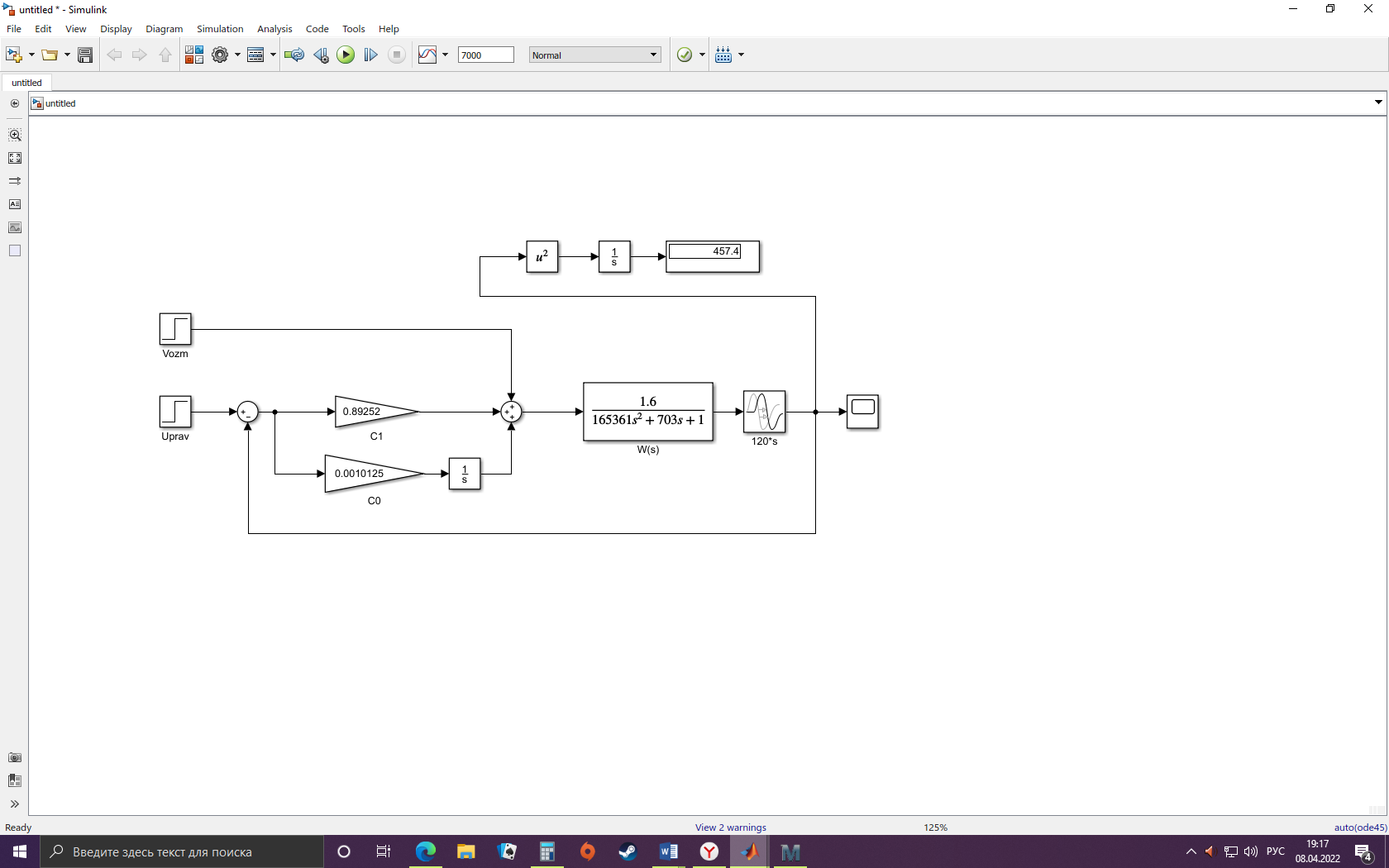
Рисунок 13 – Замкнутая система с ПИ-регулятором

Результаты выбора оптимальных настроек регулятора одноконтурной системы даны в таблице 2.

Таблица 2 – Выбор настроек регулятора одноконтурной системы

С0	С1	Интегральный квадратичный критерий
0.0011751	0.7876	463
0.0010125	0.89252	457
0.0010033	0.89693	459
0.00097471	0.91008	462

Оптимальные настройки ПИ-регулятора равны С₀ = 0,0010125, С₁ = 0,89252. Передаточная функция регулятора:

---

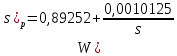
Переходные процессы в одноконтурной системе по управлению и возмущению приведены на рисунках 14, 15.



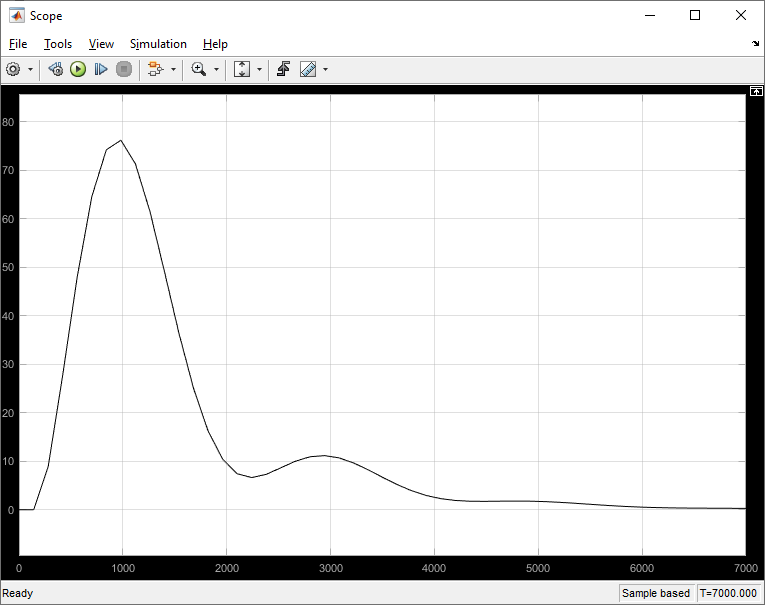
Рисунок 14. Переходный процесс в одноконтурной системе по возмущению



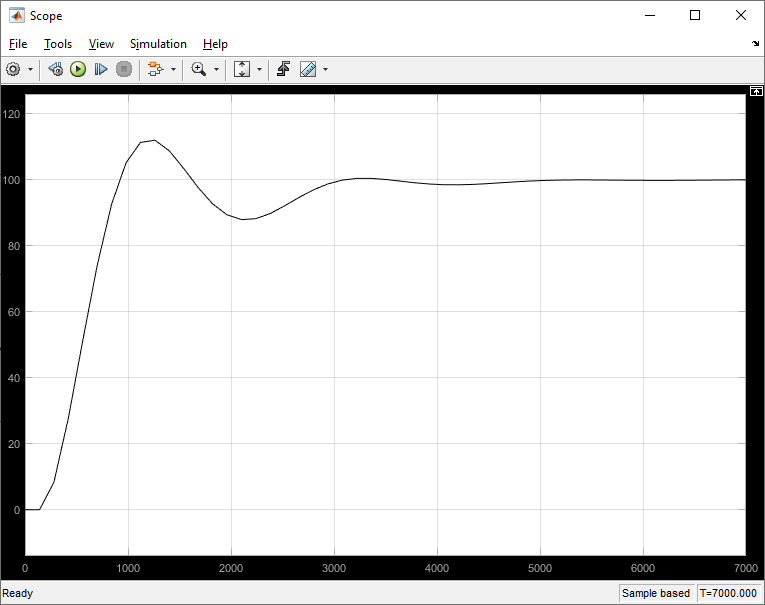
Рисунок 15. Переходный процессы в одноконтурной системе по управлению

Длительность переходного процесса по возмущению около 100 мин, степень затухания ψ =0,97, что выше заданного значения (ψ = 0,9), однако динамическое отклонение более 10 мм, что соответствует требованиям технологического процесса (отклонение не более 100 мм).

2.2.5 Расчет комбинированной системы с компенсацией возмущения по каналу расхода диэтаноламина

Основой расчета комбинированной системы регулирования является условие инвариантности, который подразумевает, что отклонение выходной координаты технологического объекта управления Y(t) под действием возмущения V(t) должно быть тождественно равно нулю.

Для случая, когда сигнал от компенсатора подается на вход объекта (рис. 12), структурная схема комбинированной системы автоматизированного регулирования преобразуется к последовательному соединению разомкнутой систему и замкнутого контура.



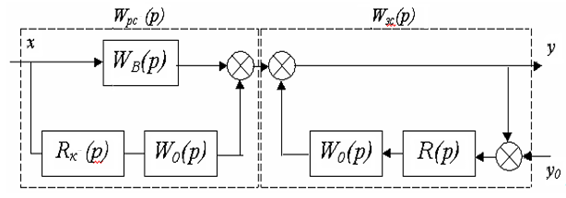
Рисунок 14 − Структурная схема комбинированной АСР при подаче компенсирующего сигнала на вход объекта

При этом:





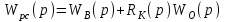
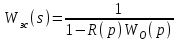
Передаточная функция комбинированной системы равна

,

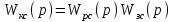а выходной сигнал системы:



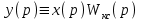
Исходя из условия инвариантности, получим:



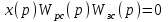
Есл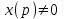и и 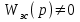, то получаем условие инвариантности в виде

---