Файл: Курс лекций санктпетербург 2002 Министерство образования рф.doc

ИНЖЕНЕРНАЯ ГРАФИКА
НаЧертательнаЯ геометриЯ

(ОСНОВЫ ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ И ЛИНЕЙНАЯ ПЕРСПЕКТИВА)
Курс лекций


САНКТ-ПЕТЕРБУРГ

2002

Министерство образования РФ

С анкт-Петербургский государственный горный институт им. Г.В.Плеханова

(технический университет)

Кафедра начертательной геометрии и графики

ИНЖЕНЕРНАЯ ГРАФИКА
НаЧертательнаЯ геометриЯ

(ОСНОВЫ ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ И ЛИНЕЙНАЯ ПЕРСПЕКТИВА)
Курс лекций


САНКТ-ПЕТЕРБУРГ

2002
УДК 622:744(075.83)
Инженерная графика. Начертательная геометрия: Курс лекций/ Санкт-Петербургский государственный горный институт. - В.М. Пашкевич, П.Г.Талалай, С.А Игнатьев, В.А. Меркулова - СПб, 2002 . – с. 64.
Курс лекций содержит разделы теоретического курса начертательной геометрии (основы ортогонального проецирования и линейной перспективы) и дополнен примерами решения задач. Основные положения курса соответствуют Государственным образовательным стандартам высшего профессионального образования для студентов направлений 650300 «Геодезия» и 650500 «Землеустройство и земельный кадастр» по дисциплинам «Инженерная графика» и «Начертательная геометрия и инженерная графика» (раздел «Начертательная геометрия» и «Линейная перспектива»). Данный курс лекций может быть использован также студентами других специальностей.

Табл. 5. Ил. 92. Библ.: 19 назв.

Научный редактор: проф. Н.Е.Бобин

Ó Санкт-Петербургский государственный

горный институт им. Г.В.Плеханова, 2002 г.

Лекция 1

ВВЕДЕНИЕ
Изготовление любой детали, строительство сооружений, разработка месторождений полезных ископаемых начинается с составления чертежей, планов и схем. Никакие словесные описания не могут заменить чертежа, который позволяет не только определить форму и размеры всех частей предмета, но и получить наглядное представление о нем.

Начертательная геометрия, как следует из названия, является одним из разделов геометрии, в котором свойства пространственных фигур изучаются по их изображениям на той или иной поверхности. Чаще всего за такую поверхность принимается плоскость.

---

Как и любая научная дисциплина, начертательная геометрия опирается на свою терминологию, которую, по мере знакомства с ней, следует хорошо усвоить, для того чтобы понимать излагаемый материал.

В геометрии вообще и в начертательной геометрии в частности каждое последующее изложение основывается на предыдущем материале. Такая особенность изучаемого предмета требует систематической, последовательной работы над ним.

ИЗ ИСТОРИИ ПРЕДМЕТА
Потребность в отображении действительности появилась у человека в самом начале его эволюционной истории. Об этом свидетельствуют многочисленные изображения на стенах пещер и камнях, на предметах и орудиях труда первобытного человека. С развитием человека совершенствовалась и техника передачи различных символов (письменности, схем, чертежей). В Древнем Китае, например, была разработана всеобъемлющая знаковая система, где каждому предмету или явлению соответствовал особый знак (иероглиф). В Древнем Египте при возведении сооружений архитекторы использовали чертежи в виде планов и фасадов.

Основные правила и методы построения различных изображений (планов зданий, земельных угодий, крепостных укреплений) по законам геометрии были разработаны в эпоху античности. В древней Греции, за 300 лет до нашей эры, мы встречаем первые шаги к научному обоснованию метода центрального проецирования. В «Оптике» Евклида содержатся 12 аксиом и 61 теорема об условиях «видения» предметов.

Расцвет классической культуры сменился застоем, и только в эпоху Возрождения в истории начертательной геометрии начинается новый период развития, главным образом, благодаря усилиям школ живописи и архитектуры Италии, Нидерландов и Германии. К этому времени относится введение целого ряда основных понятий метода проецирования.

С дальнейшим развитием архитектуры, машинного производства, горной промышленности стали предъявляться все более высокие требования к изображениям предметов, что и привело к необходимости обобщения и систематизации знаний по «теории изображений». Работа знаменитого французского геометра и инженера времен Великой французской революции Гаспара Монжа (1746 - 1818) «Geometrie Descriptive» (1798 г.) представляет собой первое систематическое изложение общего метода изображения пространственных фигур на плоскости, поднявшее начертательную геометрию на уровень самостоятельной научной дисциплины.

---

Преподавание начертательной геометрии в России началось уже в первые годы XIX века в Корпусе инженеров путей сообщения и чуть позже в Горном кадетском корпусе. Первый русский профессор начертательной геометрии Я.И.Севастьянов (1796 – 1849) в 1821 г. составил курс «Основания начертательной геометрии», ставший классическим учебным пособием по этому предмету.

Среди ученых, внесших наиболее значимый вклад в развитие начертательной геометрии, следует отметить имя академика Е.С.Федорова (1853 – 1919), преподававшего в Горном институте. На примере решения задач минералогии и кристаллографии он показал применимость методов начертательной геометрии к исследованиям закономерностей материального мира.

В настоящее время начертательная геометрия является базовой общетехнической дисциплиной, составляющей основу инженерного образования. Было бы, однако, большой ошибкой ограничивать значение начертательной геометрии лишь рамками узкого прикладного характера, как теоретической основы черчения. Ее методы дают возможность решать самые сложные проблемы в различных областях – горно-геологических науках, химии, физике и др.

МЕТОДЫ ПРОЕЦИРОВАНИЯ
В начертательной геометрии чертеж является основным инструментом решения различных пространственных задач. Поэтому к выполняемому чертежу предъявляются ряд особых требований, среди которых наиболее существенными являются следующие: чертеж должен быть наглядным, обратимым, достаточно простым и точным.

О становимся более подробно на обратимости чертежа. Под этим свойством понимается точное воспроизведение формы и размеров предмета по его изображению. Действительно для всех видов технических и горно-геологических чертежей это требование является особенно важным, так как при помощи чертежа в машиностроении изготавливается та или иная деталь, в горном деле осуществляется проходка горных выработок, в геологии – оценка запасов полезного ископаемого и т.д.

Основным методом получения изображений в начертательной геометрии является проецирование.

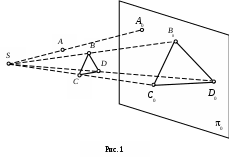
Чтобы понять сущность проецирования, обратимся к рис. 1.

Выбираем центр проецирования - произвольную точку S пространства и поверхность проецирования, не проходящую через точку S, например, плоскость проекций ₀. Для того, чтобы спроецировать некоторую точку A пространства на плоскость ₀

---

, необходимо через центр проецирования S провести проецирующую прямую SA до ее пересечения в точке A₀ с плоскостью ₀.

При этом точка A₀ называется проекцией точки A на плоскости ₀. Проекцией фигуры называется совокупность проекций всех ее точек на выбранную поверхность проецирования (например, на рис. 1 проекцией треугольника BCD на плоскости ₀ является треугольник B₀C₀D₀). Описанный метод проецирования путем проведения проецирующих прямых через точки заданной фигуры и центр проецирования, называется центральным.

В 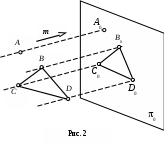случае, если проецирование осуществляется из бесконечно удаленной точки пространства (рис. 2), то все проецирующие прямые окажутся взаимно параллельными. Этот метод проецирования называется параллельным, а направление m, по которому оно осуществляется, - направлением (вектором) проецирования.

Если направление параллельного проецирования перпендикулярно плоскости проекций, то оно называется прямоугольным или ортогональным. Во всех остальных случаях параллельное проецирование называется косоугольным.

Изображения, полученные при помощи центрального проецирования, обладают хорошей наглядностью, что объясняется устройством зрительного аппарата человеческого глаза. Однако, этот метод имеет существенные недостатки, заключающиеся, во-первых, в сложности построения изображения предмета и, во-вторых, в низких метрических свойствах построенных проекций: вследствие значительных искажений, возникающих при данном методе проецирования, определить истинные размеры предмета весьма затруднительно. Поэтому этот способ имеет ограниченное применение в практике и используется, когда от чертежа требуется прежде всего наглядность.

Несмотря на то, что параллельное проецирование по сравнению с центральным дает меньшую наглядность, параллельные проекции и особенно ортогональные обладают лучшей измеримостью и простотой построения.

Задачи, решаемые методами начертательной геометрии, принято делить на метрические и позиционные.

---

Метрические задачи имеют целью определение размеров различных предметов по их изображению. К таким задачам относятся задачи по определению натуральной величины геометрических фигур, расстояний и углов между ними. В горно-геологической практике – это задачи на определение глубины и угла наклона буровых скважин, угла падения пласта полезного ископаемого, углов между осями горных выработок и т.п.

В позиционных задачах определяется взаимное расположение различных объектов: точек, прямых линий, плоскостей, пространственных фигур. К этой категории задач относятся, например, установление точки встречи буровой скважины с плоскостью залежи, построение линии пересечения кровли и подошвы пласта полезного ископаемого с горной выработкой и многие другие.

Для быстрого и удобного решения пространственных задач в начертательной геометрии используются несколько систем изображений, особенности которых приведены в таблице 1.
Таблица 1

Основные системы изображений, получаемые при помощи проецирования

Наименование	Метод проецирования	Поверхность проецирования	Особенности
Эпюр (ортогональный чертеж)	ортогональное проецирование	две или три взаимно перпендикулярные плоскости	условное совмещение плоскостей проекций с плоскостью чертежа путем их вращения
Проекции с числовыми отметками	ортогональное проецирование	плоскость	расстояние до плоскости проекций определяется числовой отметкой
Векторные (федоровские) проекции	ортогональное проецирование	плоскость	расстояние до плоскости проекций определяется вектором масштабной длины
Перспектива	центральное проецирование	плоскость, цилиндр, сфера	ограничение максимального угла между проецирующими лучами
Аксонометрическая проекция	параллельное или центральное проецирование	плоскость	проецирование вместе с осями координат

---