Файл: Курс лекций санктпетербург 2002 Министерство образования рф.doc

Итак, каждая точка плоской фигуры определяется пересечением прямых, принадлежащих двум различным пучкам параллельных линий.

Построение перспективы предмета (например, здания) проводится с изменением всех линейных размеров с учетом принятого масштаба.

После того, как начерчены ортогональные проекции фасада и плана здания (рис. 88) и построена перспектива контура плана здания (см. пример построения пер-

с 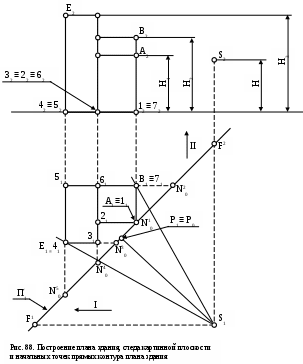пективы контура – рис. 87), построение перспективы здания осуществляется в такой последовательности (рис. 89):

через вершины (точки 1^/, 2^/, 3^/ и т.д.) проводятся тонкие вертикальные прямые (будущие ребра здания);

• 
  от точки 1^/ на проходящей через нее вертикали откладывается отрезок 1^/ - А^/ длиной Н₁, умноженный на масштаб. Поскольку ребро А лежит в плоскости картины, высота этого ребра является истинной величиной;
  
• 
  ч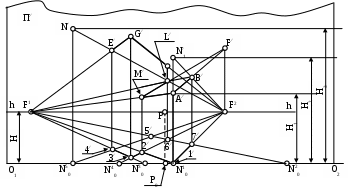
  Рис. 89. Построение перспективы здания.
  ерез точку А^/ проводится прямая в точку схода следов F¹. На этой прямой в точке пересечения с вертикалью 2^/ - М^/ находится точка М^/;
  
  
• 
  для того, чтобы получить перспективы вертикальных ребер высотой Н₃, проходящих через точки 3^/, 4^/, 5^/, и 6^/, необходимо соответственно на вертикалях из точек N⁴₀,N⁵₀,N²₀,или N³₀,отложить отрезок, равный Н₃, умноженный на масштаб. Из точекF¹ иF² через полученные точки проводятся прямые и там, где соответствующие прямые (например,F²N^/ иF¹G^/) пересекут вертикали из точек 3^/, 4^/, 5^/ и 6^/ строятся верхние точки ребер (например, E^/ и G^/), а соответственно и перспективы самих ребер.
  

Аналогично производится построение ребер высотой Н₂.

Проверкой точности построения является сходимость прямых A^/

---

B^/и M^/L^/на вертикали, проведенной через точку сходаF² (в точке F^/).

Лекция 7
АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
Аксонометрическая проекция или аксонометрия (от греч. axwn - ось и metrew - измеряю) представляет собой изображение объекта на некоторой плоскости, полученное путем проецирования объекта вместе с осями прямоугольных координат, к которым отнесена система точек этого объекта. Аксонометрические проекции обладают свойством наглядности и одновременно свойством обратимости - по таким чертежам легко представить общую форму предметов и их положение в пространстве.

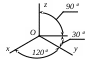
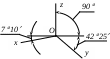
К 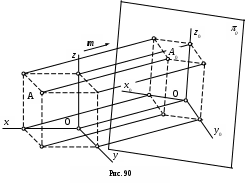ак правило, аксонометрические проекции образуются путем параллельного проецирования, причем направление проецирования не параллельно ни одной из осей проекций. На рис. 90 показано получение аксонометрической проекции некоторой точки А пространства. Указанная точка А отнесена к системе трех взаимно перпендикулярных плоскостей, пересекающихся по осям x, y и z. По направлению (вектору) m координатная система вместе с точкой А спроецирована на произвольную плоскость проекций ₀, где и получена ее аксонометрическая проекция А₀.

Если направление проецирования перпендикулярно плоскости чертежа, то аксонометрические проекции называются прямоугольными, в противном случае - косоугольными.

Проекции осей координат называются аксонометрическими осями. Отношение k длины отрезка, расположенного на аксонометрической оси, к длине отрезка в натуре называется коэффициентом искажения (числено он равен косинусу угла наклона координатных осей к плоскости проекций).

В зависимости от соотношения между коэффициентами искажения аксонометрические проекции подразделяются на:

1. 
   изометрические, если все три коэффициента искажения равны между собой (k_x=k_y=k_z);
   
2. 
   диметрические, если два коэффициента искажения равны между собой (например, k_x=k_z¹k_y);
   
3. 
   триметрические, если все коэффициенты искажения различны (k_x¹k_y¹k_z).
   

В практике построений с целью обеспечения максимальной наглядности используются лишь некоторые определенные комбинации направлений аксонометрических осей и коэффициентов искажения (табл. 4).

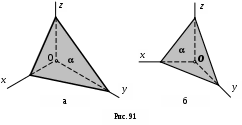
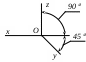
На рис. 91,а построена прямоугольная изометрическая проекция плоскости α, а на рис. 91,б - ее косоугольная фронтальная диметрическая проекция.

---

Таблица 4

Аксонометрические проекции

Вид проекции	Расположение аксонометрических осей	Особенности построения окружностей*	Коэфф. искажения
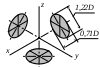Прямоугольная изометрическая			kx=ky=kz=0,82 (допускается округлять до 1,0)
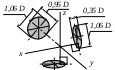Прямоугольная диметрическая			ky=0,47; kx=kz=0,94 (допускается округлять ky=0,5; kx=kz=1,0)
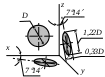Косоугольная фронтальная диметрическая			ky=0,5; kx=kz=1,0

---

* D – диаметр изображаемой окружности

ВМЕСТО ЗАКЛЮЧЕНИЯ:

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ И МАШИННАЯ ГРАФИКА

Так как предметом начертательной геометрии является изучение методов построения различных пространственных форм на той или иной поверхности, то ее возможности как науки значительно расширились с развитием вычислительной техники и систем программирования.

Широкое использование персональных компьютеров в инженерной практике привело буквально к перевороту в области выполнения чертежей и рождению новой дисциплины – машинной графики, занимающейся созданием, хранением и обработкой различных изображений при помощи электронно-вычислительных устройств.

Все графические форматы современных программ машинной графики можно разделить на две категории: растровые и векторные.

Элементами растровой графики являются небольшие точки, называемые пикселями. В память компьютера вводятся данные о цвете и яркости каждого пикселя. Изображения растровой графики хранятся с фиксированным разрешением, поэтому при увеличении изображения в нем возможны искажения. Растровой графикой лучше всего пользоваться для создания изображений, содержащих тонкие оттенки или очень мелкие детали.

В противоположность растровой графике, векторная графика хранится в виде команд, которые описывают размеры и форму каждого графического объекта (линии, окружности, многоугольника и т.д.), являющегося элементом изображения. Разрешение векторного изображения не фиксировано. Изображение можно увеличивать или уменьшать, не ухудшая его качества, поэтому векторной графикой пользуются, когда необходимо создавать контурные изображения, т.е. изображения, применяющиеся в основном в начертательной геометрии и инженерной графике.

Растровая графика требует значительно больше пространства на носителях информации (жестком или флоппи диске), так как для нее необходима информация о каждом пикселе, отображаемом на экране. С другой стороны, представление векторной графики на экране персонального компьютера занимает иногда больше времени, так как процессор должен еще нарисовать его, тогда как растровые изображения просто загружаются непосредственно в память.

---

В
Таблица 5

Чертежно-конструкторские и графические редакторы

Программа	Расширение файла	Тип графики
AutoCAD	dfx	векторная
AutoCAD Plot	plt	векторная
CorelDRAW	cdr	векторная
Micrografx Designer and Micrografx Draw	drw	векторная
PC Paintbrush	pcx	растровая
Portable Network Graphics	png	растровая
Компас-График	cad, frg	векторная

настоящее время на мировом рынке систем автоматизированного проектирования имеется большое количество чертежно-конструкторских и графических редакторов (табл. 5). Главным преимуществом отечественной разработки «Компас-График» является возможность компьютерного проектирования чертежей и сопутствующей документации в полном соответствии с российскими стандартами. Правда, при помощи этой программы невозможно объединять графические файлы с другими Windows-приложениями.

Зарубежные графические программы поддерживают стандарт OLE (ObjectLinkingandEmbedding), позволяющий импортировать или экспортировать графические объекты из одной программы в другую, связывая отдельные документы в один.

Иллюстрации настоящего конспекта лекций созданы при помощи графических средств, встроенных непосредственно в текстовый редактор Word. Основным понятием в этом редакторе является понятие объекта, под которым понимается элемент изображения наиболее распространенных геометрических форм (прямой, окружности, прямоугольника и т.д.).

Основной принцип создания изображений заключается в использовании простых объектов как элементов более сложной конфигурации путем их стыковки и взаимного наложения. Объекты группируются, что позволяет редактировать и перемещать всю группу изображений как единого объекта.

Т 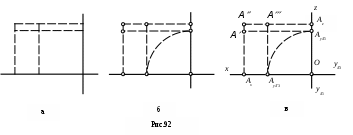ехника рисования очевидна из следующего примера (рис. 92): сначала создана группа прямых линий (рис. 92,

---