Файл: Курс лекций санктпетербург 2002 Министерство образования рф.doc

Плоскости проекций ₁, ₂ и ₃ являются неограниченными поверхностями и при взаимном пересечении делят пространство на восемь трехгранных углов, или октантов (от лат. octans - восьмая часть).

Нумерация октантов в полупространствах приведена на рис. 12. Знаки координат в каждом из октантов указаны в табл. 2.

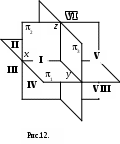
Таблица 2

Знаки прямоугольных координат в различных октантах

№ октанта	x	y	z	Положение в пространстве
I	+	+	+	ЛПВ
II	+	-	+	ЛЗВ
III	+	-	-	ЛЗН
IV	+	+	-	ЛПН
V	-	+	+	Пр.ПВ
VI	-	-	+	Пр.ЗВ
VII	-	-	-	Пр.ЗН
VIII	-	+	-	Пр.ПН

Обозначения в таблице: Л – левый октант; Пр. – правый октант; П – передний октант;

З – задний октант; В – верхний октант; Н – нижний октант.

Лекция 2
ПРОЕЦИРОВАНИЕ ПРЯМОЙ ЛИНИИ

П

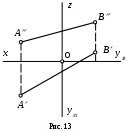
рямую линию можно рассматривать как совокупность точек. Из школьного курса геометрии известно, что через две точки можно провести прямую и при том только одну.

Пусть нам даны на эпюре две точки А и В (рис. 13). Две проекции каждой из этих точек однозначно определяют их положение в пространстве. Если мы соединим одноименные проекции точек, то получим

проекции прямой. Точки А и В ограничивают отрезок прямой и определяют положение этой прямой как бесконечной линии.

Таким образом, прямая линия на эпюре может быть задана двумя ее проекциями. По двум проекциям отрезка всегда можно построить его третью проекцию, и притом только одну.

Если прямая не параллельна ни одной из плоскостей проекций, то она пересекает все плоскости проекций и не проецируется ни на одну из них в натуральную величину. Такую прямую называют прямой общего положения. Ни одна из ее проекций не параллельна осям координат. Пример такой прямой изображен на рис. 13.

точкА на прямой

Точка принадлежит прямой линии, если ее проекции лежат на одноименных проекциях этой линии.

Е

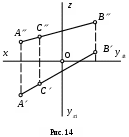сли на прямой АВ мы выберем какую- либо точку С, то проекции этой точки будут лежать на одноименных проекциях прямой (рис. 14).

Вспомним опять школьный курс геометрии: стороны плоского угла делятся параллельными прямыми в пропорциональном отношении. Поэтому если точка делит отрезок прямой в каком-то отношении, то ее проекции делят соответствующие проекции прямой в том же отношении:

.
ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ
Прямая, параллельная одной или двум плоскостям проекций, называется прямой частного положения.

Если прямая параллельна одной плоскости проекций, то одна проекция такой прямой проецируется в натуральную величину, а две другие параллельны осям проекций.

Рассмотрим случаи, когда прямая параллельна одной плоскости проекций.

Г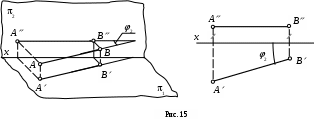 оризонтальная прямая - прямая, параллельная плоскости ₁ (рис. 15).

Все точки такой прямой удалены от плоскости проекций ₁ на одинаковое расстояние, следовательно, у всех точек такой прямой координата z будет одинакова.

Ф

ронтальная АВ и профильная АВ проекции горизонтальной прямой всегда перпендикулярны оси z. Горизонтальная проекция отрезка горизонтальной прямой АВ равна его натуральной величине. Угол между горизонтальной проекцией горизонтальной прямой

АВ иосью x является углом наклона ₂ этой прямой к фронтальной плоскости проекций ₂.

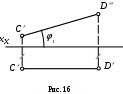
2) Фронтальная прямая - прямая, параллельная плоскости ₂ (рис. 16).

Фронтальная проекция отрезка фронтальной прямой равна его натуральной величине; горизонтальная и профильная проекции фронтальной прямой всегдаперпендикулярны оси y.

У

гол ₁ между фронтальной проекцией фронтальной прямой и осью x является углом между фронтальной прямой и горизонтальной плоскостью проекций.

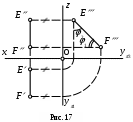
3) Профильная прямая - прямая, параллельная плоскости ₃ (рис. 17).

Профильная проекция отрезка профильной прямой равна его натуральной величине; горизонтальная и фронтальная проекции профильной прямой всегда перпендикулярны оси x.

Угол ₁ между профильной проекцией профильной прямой и осью y является углом наклона прямой к горизонтальной плоскости проекций; угол ₂ между профильной проекцией прямой и осью z - углом наклона прямой к фронтальной плоскости проекций.

Если прямая параллельна двум плоскостям проекций (т.е. перпендикулярна третьей плоскости проекций), то на эти две плоскости проекций прямая проецируется в натуральную величину, а третья проекция представляет собой точку. В зависимости от расположения различают следующие прямые, перпендикулярные плоскостям проекций.

1) Горизонтально-проецирующая прямая – прямая, перпендикулярная плоскости ₁ (прямая АВ на рис. 18).

Фронтальная и профильная проекции отрезка горизонтально-проецирующей прямой равны его натуральной величине, а ее горизонтальная проекция представляет собой точку.

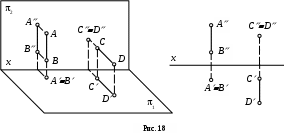
2) Фронтально-проецирующая прямая - прямая, перпендикулярная плоскости ₂ (прямая CD на рис. 18).

Г
x

x

оризонтальная и профильная проекции отрезка фронтально-проецирующей прямой равны его натуральной величине, а ее фронтальная проекция представляет собой точку.

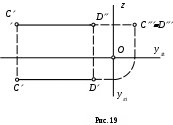
3) Профильно-проецирующая прямая – прямая, перпендикулярная плоскости ₃(рис. 19).

Горизонтальная и фронтальная проекции отрезка профильно-проецирующей прямой равны его натуральной величине, профильная проекция профильно-проецирующей прямой представляет собой точку.

Определение натуральной величины отрезка прямой общего положения методом прямоугольного треугольника
Ортогональная проекция отрезка прямой общего положения на любую плоскость проекций всегда меньше длины самого отрезка. Для определения натуральной величины отрезка прямой служит метод прямоугольного треугольника, который заключается в следующем.

Предположим, что точки А и В лежат в I октанте (рис. 20, а). Соединим эти точки и получим отрезок некоторой прямой АВ.

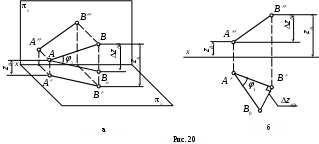
Из точки А проведем линию параллельную АВ, которая в пересечении с линией проекционной связи даст точку В₀.

Рассмотрим прямоугольный треугольник АВВ_О:

гипотенуза АВ определяет истинную величину этого отрезка;
катет АВ₀ равен горизонтальной проекцией АВ;
катет ВВ₀ равен z = z_В – z_А.

На ортогональном чертеже оказывается достаточно данных для построения на чертеже треугольника, равного рассмотренному (рис. 20, б). Для этого к горизонтальной проекции АВ «пристроен» второй катет - разность координат z. Гипотенуза построенного треугольника есть натуральная величина отрезка АВ.

Е

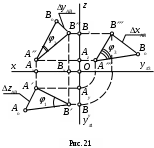
сли прямоугольный треугольник строится на фронтальной проекции, то второй катет окажется равным разности координат y (табл. 3). Для треугольника, построенного на профильной проекции, вторым катетом будет x (рис. 21).

Координаты концов отрезка могут иметь разные знаки. Тогда разность координат определяется с учетом знака. Например, если координата z точки А положительная, а точки В отрицательная, то разность координат будет равна

z_АВ = z_A – (-z_B) = z_A + z_B.

Таблица 3

Геометрические элементы при определении истинной величины отрезка прямой методом прямоугольного треугольника

Проекция отрезка прямой, выбираемая в качестве первого катета треугольника	Разность координат, откладываемая в качестве второго катета	Плоскость проекций, к которой определяется угол наклона	Обозначение угла наклона
горизонтальная: АВ	z_АВ=A_zB_z	₁	₁
фронтальная: АВ	y_AB=A_yB_y	₂	₂
профильная: АВ	x_AB=A_xB_x	₃	₃

В общем случае натуральная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка прямой, а вторым - разность «третьих» координат.

Угол наклона прямой к плоскости проекций – это угол между прямой и ее проекцией. Следовательно, определяя истинную величину отрезка прямой методом прямоугольного треугольника, одновременно можно найти и угол ее наклона к плоскости проекций (₁, ₂, ₃). Угол между гипотенузой и соответствующей проекцией отрезка равен углу наклона этой прямой к данной плоскости проекций.

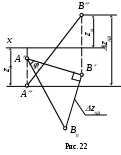
Пример 3. Определить истинную величину отрезка АВ и угол наклона к плоскости ₁ (рис. 22).
1. По таблице 3 определяем, что для нахождения угла наклона к плоскости ₁ надо построить прямоугольный треугольник, в котором одним катетом будет горизонтальная проекция отрезка АВ, а вторым – разность координат по оси z.

2. Определяем координаты по оси z точек А и В и их разность:

z_АВ = z_В – (-z_А) = z_В + z_А.

3. Строим прямоугольный треугольник, в котором за катет принимаем горизонтальную проекцию АВ. В качестве второго катета откладываем расстояние, равное z_АВ.

4. Гипотенуза построенного треугольника есть истинная величина отрезка АВ, а угол при вершине А (угол ₁) – угол наклона прямой к плоскости ₁.

Лекция 3
СЛЕДЫ ПРЯМОЙ
Следом прямой называется точка пересечения прямой линии с плоскостью проекций (является точкой частного положения – лежит в плоскости проекций).

Прямая общего положения пересекает все три плоскости проекций и, следовательно, имеет три следа. Прямая линия частного положения не имеет следа на плоскости проекций, если она параллельна этой плоскости.

Выберем две точки: точку М, лежащую в плоскости проекций _1, и точку N – в плоскости проекций ₂ (рис. 23, а). Через эти точки проведем прямую.