Файл: Курс лекций санктпетербург 2002 Министерство образования рф.doc

ВЗАМНО ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ

Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную другой плоскости.

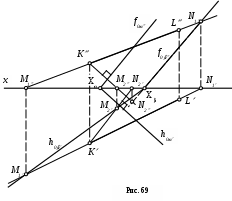
На рис. 69 дано построение плоскости , перпендикулярной плоскости  и проходящей через прямую KL. Из любой точки прямой KL, например, из точки К, проводим перпендикуляр к заданной плоскости . Строим следы прямой KL и перпендикуляра: проекции горизонтального и фронтального следов прямой KL (M₁ и M₁, N₁ и N₁) и перпендикуляра (M₂ и M₂, N₂ и N₂) .

Через горизонтальные проекции горизонтальных следов M₁и M₂ проводим горизонтальный след плоскости ; через фронтальные проекции фронтальных следов N₁ и N₂ - фронтальный след . Проверяем правильность построений: следы h_0 и f_0 должны пересечься в точке схода следов Х_ на оси x.

Таким образом, плоскость  перпендикулярна плоскости  (однако их одноименные следы в общем случае не перпендикулярны друг другу).


Лекция 6

ОСНОВЫ ЛИНЕЙНОЙ ПЕРСПЕКТИВЫ.

СУЩНОСТЬ МЕТОДА.
П 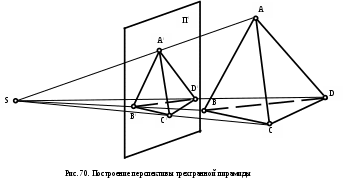ерспектива представляет собой способ изображения тел и плоских фигур, основанный на применении центрального проецирования. Для построения перспективы предмета из некоторой точки S (точки зрения) проводят лучи ко всем точкам изображаемого предмета. На пути проецирующих лучей располагают поверхность П^’ (картину), на которой строят искомое изображение, определяя точки пересечения лучей с поверхностью картины (рис.70).

Метод отличается хорошей наглядностью, перспектива предмета соответствует тому, что видит глаз человека (передает кажущиеся изменения формы и размеры предмета, вызванные его расположением и удаленностью от наблюдателя), поэтому этот метод нашел широкое распространение в архитектурном проектировании, в строительном деле, геодезии и других прикладных науках.

В зависимости от поверхности, на которую производится проецирование, следует различать перспективу плоскую (

---

П^/ - плоскость), панорамную (П^/ - цилиндрическая поверхность) и купольную (П^/ - сфера).

Для того, чтобы обеспечить взаимную однозначность между точками изображаемого предмета и точками на картинной плоскости (сделать изображение обратимым), заданную точку А ортогонально проецируют на горизонтальную плоскость П₁, а затем на плоскости картины П^/ определяют перспективные проекции А^/и А₁^/ соответственно точки А и ее горизонтальной проекции А₁. Проекция А^/ точки А называется перспективной проекцией (перспективой) точки А, а проекция А₁^/ - вторичной проекцией точки А. На плоскости П^/ проекции А^/и А₁^/ принадлежат одной вертикальной прямой, так как лежат в лучевой плоскости, перпендикулярной плоскости П₁.
И 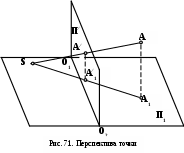з рис. 71 и 72 видно, что по заданным проекциям А^/и А₁^/ и точке S можно однозначно определить положение точки А в пространстве.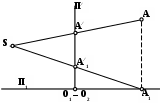




Рис. 72. Построение перспективы и вторичной проекции точки

СИСТЕМА ПЛОСКОСТЕЙ ЛИНЕЙНОЙ ПЕРСПЕКТИВЫ

П 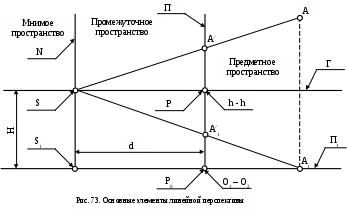ри рассмотрении метода линейной перспективы следует различать следующие основные точки, линии, плоскости и части пространства (рис.73):

S– точка зрения (центр проецирования);

S₁ – основание точки зрения (точка стояния);

P – главная точка стояния;

P₀ – основание главной точки картины;

П₁ – предметная плоскость;

П^/ - картинная плоскость;

Г – плоскость горизонта;

N– плоскость, параллельная П^/ и проходящая через точку S, - нейтральная

плоскость;

O₁ – O₂ – основание картины;

h – h– линия горизонта;

S – P – главный луч картины;

d– главное расстояние;

H

---

– высота горизонта.

Пространство до плоскости N называется мнимым, между плоскостями N и П^/ – промежуточным, а за плоскостью П^/ – предметным.

Для построения перспективы необходимо знать положение точкиS относительно плоскостей П^/ и П₁.


ПЕРСПЕКТИВЫ ТОЧЕК, РАСПОЛОЖЕННЫХ В РАЗЛИЧНЫХ

ЧАСТЯХ ПРОСТРАНСТВА.
Рассмотрим точку Ав предметном пространстве и проследим за тем, как будут изменяться положения ее перспективы А^/ и вторичной проекции А₁^/ при движении точки А вдоль проецирующего луча SA (рис.74).

Из рис. 74 видно, что положение точки в той или иной части пространства относительно плоскости картины П^/ определяется положением ее вторичной проекции в плоскости картины П^/ относительно линии горизонтаh – h и линии основания картины O₁ – O₂.

Вторичная проекция бесконечно удаленной точки предметного пространства (точка F) должна находиться на линии горизонта (линии h – h).

Если точки равноудалены от плоскости картины, то их вторичные проекции находятся на одинаковом расстоянии от основания картины (линии O₁ – О₂).




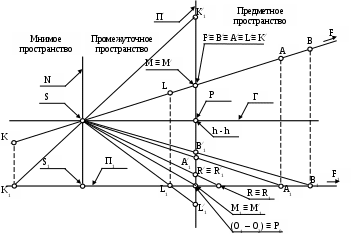
Рис. 74. Перспективы и вторичные проекции точек, расположенных в разных частях пространства:

F – бесконечно удаленная точка предметного пространства;

А и В – точки, находящиеся в предметном пространстве;

R – точка, лежащая в предметной плоскости;

М – точка, лежащая в плоскости картины;

L – точка, лежащая в промежуточном пространстве;

К - точка, лежащая в мнимом пространстве.



При удалении точки, находящейся в предметном пространстве, от плоскости картины П^/ расстояние от ее вторичной проекции А₁^/ до основания картины

(линии O₁ – O₂) увеличивается, а вторичные проекции точек находятся между основанием картины (линией

---

O₁ – O₂) и линией горизонта картиныh – h(точки А и В).

Вторичные проекции точек, расположенных в промежуточном пространстве (точка L), находятся ниже основания картины (линии O₁ – O₂), а расположенных в мнимом пространстве (точка К) – выше линии горизонта.

Вторичная проекция точки, лежащей в плоскости картины П^/ (точка М), находится на основании картины (линии O₁ – O₂).

На основе изложенного материала могут решаться прямые и обратные задачи по построению наглядного изображения (изображение в косоугольной фронтальной диметрической аксонометрической проекции) положения точки в пространстве или ее перспективы и вторичной проекции.

Пример 7. Построить положение точек A, B, C и D в пространстве по заданным их перспективам и вторичным проекциям (прямая задача) и построение перспектив и вторичных проекций по заданному положению точек (обратная задача) (рис. 75).




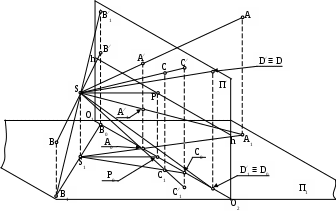
Рис. 75. Построение положения точек по заданным их перспективам и вторичным проекциям.


Алгоритм решения задач следующий. Сначала задается положение предметной плоскости П₁ и плоскости картины П^∕, строится линия начала картины(О₁ – О₂). По заданным параметрам высоты горизонтаH и главного расстояния d строится положение точки зрения S относительно плоскости картины П^∕ и предметной плоскости П₁. Строятся основание точки зрения S₁ , линия горизонта (h - h ), главная точка картины P и основание главной точки картины P₀.

• 
  прямая задача (на примере построения точки А) (см. рис. 75).
  

1. 
   Линия проекционной связи проекций А^∕ и А^∕₁ продлевается в плоскости картины П^∕ до пересечения с линией начала картины (О₁ – О₂) и через полученную точку А₀ и точку стояния S₁ проводим след лучевой проецирующей плоскости;
   
2. 
   Через точку зрения S и вторичную проекцию точки А^∕₁ проводится луч до пересечения с продолжением линии (А₀ - S₁): полученная точка пересечения А₁ – это проекция точки А на предметной плоскости;
   
3. 
   Точка А найдется на пересечении луча (S - А^∕) с вертикальной линией проекционной связи из точки А₁;
   

---

• 
  обратная задача (на примере построения точки В) (см. рис. 75).
  

1. 
   Из точки В опускается вертикальная линия проекционной связи на предметную плоскость П₁ – получаем проекцию точки на предметной плоскости В₁. Проводим след лучевой проецирующей плоскости через точки В₁ и S₁;
   
2. 
   В точке пересечения линии (В₁ - S₁) с линией начала картины (О₁ – О₂) получаем точку В₀ – проекцию перспективы и вторичной проекции точки В на линии начала картины (О₁ – О₂). Из точки В₀ в плоскости картины П^∕ восстанавливаем вертикальную линию проекционной связи;
   
3. 
   Перспектива точки В^∕ найдется в точке пересечения вышеуказанной линии проекционной связи с лучом (S - В), а вторичная проекция В^∕₁ - с лучом (S – В₁).
   

ПЕРСПЕКТИВА ПРЯМОЙ ЛИНИИ.
П 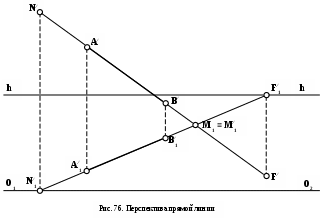ерспективное изображение прямой обратимо, если оно дополнено вторичной проекцией. На рис.76 перспектива прямой АВ и ее вторичная проекция определены перспективами и вторичными проекциями двух ее точек А и В.

Имея А^/В^/ и А₁^/ В₁^/, можно определить две характерные точки прямой:

F^/ - перспектива бесконечно удаленной точки F, принадлежащей прямой АВ; F^/ находится на пересечении линии проекционной с из F^/ с продолжением прямой А^/В^/ (вторичная проекция F₁^/ точки F находится как точка пересечения А₁^/ В₁^/ с линией горизонта h – h);

N^/ - перспектива начала прямой (началом прямой принято называть точку пересечения прямой с плоскостью картины); N^/находится на пересечении линии проекционной с из N^/ с продолжением прямой А^/В^/ (вторичная проекция N₁^/ точки N находится как точка пересечения А₁^/ В₁^/ с линией начала картины

---