Файл: Курс лекций санктпетербург 2002 Министерство образования рф.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 136
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
O1 –O2).
Точками F/ и N/ обычно пользуются при построении перспективы различных предметов.
П
Рис. 69. Положения прямой в пространстве: а – нисходящая прямая; б – восходящая прямая;
в – горизонтальная прямая; г – прямая, перпендикулярная плоскости картины;
д – прямая, перпендикулярная предметной плоскости; е – прямая, параллельная
плоскости картины; ж – прямая, параллельная плоскости картины и предметной плоскости
 оложение перспективы несобственной точки прямой на картине (F/) позволяет судить о положении прямой в пространстве (рис.77):
оложение перспективы несобственной точки прямой на картине (F/) позволяет судить о положении прямой в пространстве (рис.77):
если точка F/ оказалась над линией горизонта, то прямая – восходящая
(рис.77, а);
(рис.77, б);
 Пример 8. По положению перспектив и вторичных проекций конечных точек А и В отрезка построить положение прямой АВ в пространстве. Построить характерные точки прямой: начало прямой N и точку схода прямой F (рис.78).
Пример 8. По положению перспектив и вторичных проекций конечных точек А и В отрезка построить положение прямой АВ в пространстве. Построить характерные точки прямой: начало прямой N и точку схода прямой F (рис.78).
Рис. 78. Построение положения прямой AB и ее характерных точек : N – начала прямой
и F – бесконечно удаленной точки прямой по заданным перспективам и вторичным проекциям конечных точек отрезка.
Алгоритм решения задачи. Задается положение предметной плоскости П1 и плоскости картины П∕, строится линия начала картины (О1 – О2). По заданным параметрам высоты горизонтаH и главного расстояния
d строится положение точки зрения S относительно плоскости картины П∕ и предметной плоскости П1. Строятся основание точки зрения S1 , линия горизонта (h - h ), главная точка картины P и основание главной точки картины P0.
(О1 – О2), получаем вторичную проекцию начала прямой N∕1. Перспектива начала прямой N∕ найдется как точка пересечения вертикальной линии проекционной связи из точки N∕1 с продолжением перспективы прямой А∕В∕. Точка начала прямой N как точка, лежащая в плоскости картины, совпадает с ее перспективой N ≡ N∕;
(h – h), получаем вторичную проекцию бесконечно удаленной точки прямой F∕1. Перспектива бесконечно удаленной точки прямой F∕ найдется как точка пересечения вертикальной линии проекционной связи из точки F∕1 с продолжением перспективы прямой А∕В∕. Бесконечно удаленная точка прямой F как точка, лежащая в плоскости картины, совпадает с ее перспективой F ≡ F∕;
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
Параллельные прямые
Перспективы параллельных прямых пересекаются. Точка пересечения связки параллельных прямых называется точкой схода ( см. точку F/ на
рис. 80).
Точка схода горизонтальных параллельных прямых лежит на линии горизонта (рис.81, а).
Если горизонтальные параллельные прямые перпендикулярны к плоскости картины (П/), то точкой схода их служит главная точка картины (Р) (рис.81, б).
Точка схода параллельных прямых, лежащих в предметной плоскости П1,
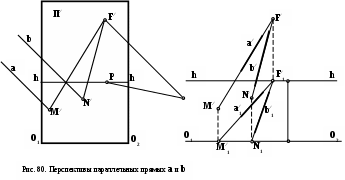
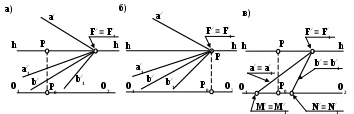
Рис. 81. Положения точки схода горизонтальных параллельных прямых:
а – прямые расположены параллельно предметной плоскости П1;
б – прямые перпендикулярны плоскости картины П⁄;
в – прямые лежат в предметной плоскости П1.
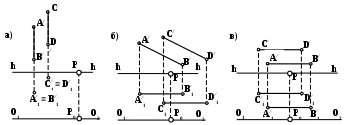
Рис. 82. Положение проекций параллельных прямых, параллельных плоскости картины П⁄:
а - прямые перпендикулярны предметной плоскости П1;
б – прямые расположены под углом к предметной плоскости П1;
в - прямые параллельны предметной плоскости П1.
находится на линии горизонта (рис.81, в).
Перспективы и вторичные проекции параллельных прямых параллельны, если прямые параллельны плоскости картины (П/) (рис.82).
Пересекающиеся и скрещивающиеся прямые
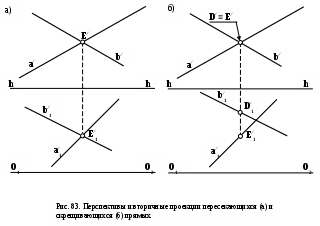
Если две прямые имеют общую точку, то точки пересечения их перспектив и вторичных проекций на плоскости картины должны лежать на общем перпендикуляре к линии горизонта (h – h), а прямые являются пересекающимися
(рис.83, а).
Если прямые не имеют общей точки, а их перспективы и вторичные проекции пересекаются, то такие прямые являются скрещивающимися (рис.83, б).
ВЫБОР ТОЧКИ И УГЛА ЗРЕНИЯ. ОРИЕНТИРОВКА КАРТИНЫ
Для того, чтобы обеспечить удачное перспективное изображение предмета, рекомендуется руководствоваться следующими правилами, выработанными практикой.
У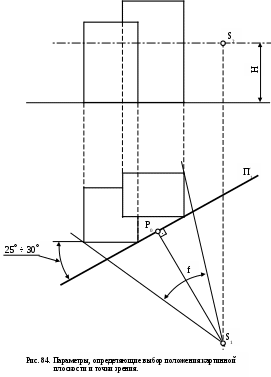 гол между проецирующими лучами, направленными в крайние точки плана предмета –
гол между проецирующими лучами, направленными в крайние точки плана предмета –
угол зрения «f» (рис. 84) должен составлять от 180 до 530. Оптимальное значение угла зрения равно 280. Если вертикальные размеры
предмета больше его длины, то точку зрения S следует перенести от картины П/ на полторы – две высоты предмета, чтобы угол зрения в вертикальной плоскости оказался в допустимых размерах, рекомендованных для угла «f».
2. Картинную плоскость П/ ориентируют так, чтобы:
а) главная Р точка оказалась в пределах средней трети угла зренияf;
б) горизонтальный след П/1 картинной плоскости с одной из сторон плана
предмета составлял от 25 до 30 градусов.
Боковой фасад при этом получит сильное перспективное сокращение. Целесообразно кроме того, картинную плоскость совместить с одним из ребер предмета, которое на перспективной проекции изобразится в истинном размере.
3. Высоту горизонта обычно принимают на уровне глаз человека, стоящего на земле, т.е. Н = 1,5 ÷ 1,7 м. При изображении застройки большого района высоту горизонта берут равной Н = 100 м и более. Такая перспектива называется перспективой с птичьего полета.
МЕТОДЫ ПОСТРОЕНИЯ ПЕРСПЕКТИВЫ
РАДИАЛЬНЫЙ МЕТОД
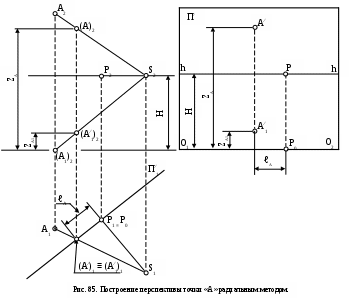
Сущность этого метода заключается в определении точек пересечения лучей с картинной плоскостью (рис. 85).
Перспектива А/ и вторичная проекция А/1 точки А на плоскости картины П/ строятся на координатах ZA, ZA1 и ℓA. Координаты ZA и ZA1 – это высотные отметки (расстояние от предметной плоскости) фронтальных проекций (А/)2 и (А/1)2 точек пересечения проекционных лучей S2А2 и S2(А1)2 из точки зрения S на точку А и ее горизонтальную проекцию А1 с плоскостью картины. Координата ℓA – это расстояние на плане (в предметной плоскости) между линией РР0 и проекцией линии пересечения лучевой плоскости на точку А с плоскостью картины.
МЕТОД АРХИТЕКТОРОВ
Данный метод построения перспективы основан на использовании точек схода параллельных прямых.
Сущность рассматриваемого метода может быть показана на примере построения перспективы фигуры, расположенной на горизонтальной плоскости
(рис. 86):
мых (направления Iи II). Определяются перспективы несобственных точек (F11иF12) каждого из пучков. ТочкаF11 является перспективой несобственной точки пучка параллельных прямых направления I, а точкаF12 является перспективой несобственной точки пучка параллельных прямых направления II. Обе точки найдены при помощи лучей S1F11 и S1F12, параллельных соответственно направлениям Iи II;
Точками F/ и N/ обычно пользуются при построении перспективы различных предметов.
П
Рис. 69. Положения прямой в пространстве: а – нисходящая прямая; б – восходящая прямая;
в – горизонтальная прямая; г – прямая, перпендикулярная плоскости картины;
д – прямая, перпендикулярная предметной плоскости; е – прямая, параллельная
плоскости картины; ж – прямая, параллельная плоскости картины и предметной плоскости
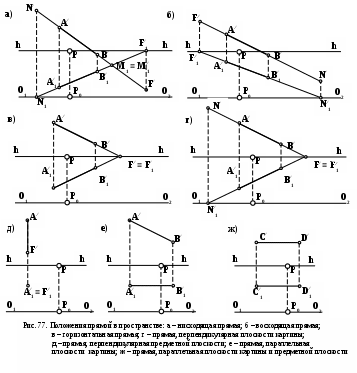
 оложение перспективы несобственной точки прямой на картине (F/) позволяет судить о положении прямой в пространстве (рис.77):
оложение перспективы несобственной точки прямой на картине (F/) позволяет судить о положении прямой в пространстве (рис.77): если точка F/ оказалась над линией горизонта, то прямая – восходящая
(рис.77, а);
-
если точка F/ оказалась под линией горизонта, то прямая – нисходящая
(рис.77, б);
-
- если точка F/ находится на линии горизонта, то прямая расположена горизонтально, параллельно предметной плоскости П1 (рис.77, в); -
если точка F/ совпадает с главной точкой картины (Р), то прямая перпендикулярна плоскости картины П/ (рис.77, г); -
в том случае, когда прямая перпендикулярна предметной плоскости (П1) ее вторичная проекция становится точкой (рис.77, д); -
когда прямая параллельна плоскости картины (П/), ее вторичная проекция параллельна основанию картины(O1 –O2) (рис.77, е).
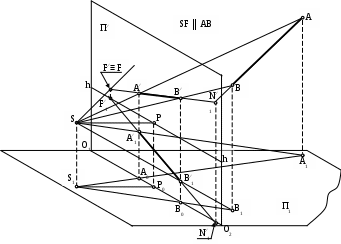
 Пример 8. По положению перспектив и вторичных проекций конечных точек А и В отрезка построить положение прямой АВ в пространстве. Построить характерные точки прямой: начало прямой N и точку схода прямой F (рис.78).
Пример 8. По положению перспектив и вторичных проекций конечных точек А и В отрезка построить положение прямой АВ в пространстве. Построить характерные точки прямой: начало прямой N и точку схода прямой F (рис.78). Рис. 78. Построение положения прямой AB и ее характерных точек : N – начала прямой
и F – бесконечно удаленной точки прямой по заданным перспективам и вторичным проекциям конечных точек отрезка.
Алгоритм решения задачи. Задается положение предметной плоскости П1 и плоскости картины П∕, строится линия начала картины (О1 – О2). По заданным параметрам высоты горизонтаH и главного расстояния
d строится положение точки зрения S относительно плоскости картины П∕ и предметной плоскости П1. Строятся основание точки зрения S1 , линия горизонта (h - h ), главная точка картины P и основание главной точки картины P0.
-
По алгоритму решения задачи, приведенному в предыдущем примере (см. рис.77), строятся точки А и В и прямая АВ; -
Соединив перспективы точек А∕ и В∕ получаем перспективу прямой А∕В∕, а соединяя вторичные проекции точек А∕1 и В∕1 получаем вторичную проекцию прямой А∕1В∕1; -
Продолжив вторичную проекцию прямой А∕1В∕1 до пересечения с линией начала картины
(О1 – О2), получаем вторичную проекцию начала прямой N∕1. Перспектива начала прямой N∕ найдется как точка пересечения вертикальной линии проекционной связи из точки N∕1 с продолжением перспективы прямой А∕В∕. Точка начала прямой N как точка, лежащая в плоскости картины, совпадает с ее перспективой N ≡ N∕;
-
Продолжив вторичную проекцию прямой А∕1В∕1 до пересечения с линией горизонта
(h – h), получаем вторичную проекцию бесконечно удаленной точки прямой F∕1. Перспектива бесконечно удаленной точки прямой F∕ найдется как точка пересечения вертикальной линии проекционной связи из точки F∕1 с продолжением перспективы прямой А∕В∕. Бесконечно удаленная точка прямой F как точка, лежащая в плоскости картины, совпадает с ее перспективой F ≡ F∕;
-
Правильность и корректность выполненных построений проверяется следующим образом:
-
прямая АВ в своем продолжении обязательно должна пройти через точку N; -
прямая, проведенная через точки S и F, должна быть параллельна построенной прямой АВ;
-
Если конечные точки прямой лежат в предметной части пространства или в промежуточном пространстве, то перспектива и вторичная проекция прямой выполняются сплошными основными линиями, проводимыми соответственно между перспективами и вторичными проекциями конечных точек прямой (см. рис. 78); -
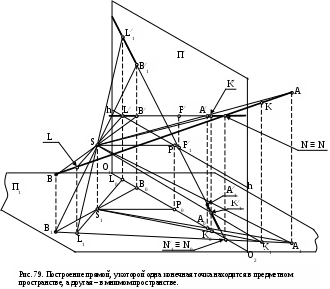
Если одна из точек прямой расположена в мнимом пространстве, то перспектива и вторичная проекция прямой выполняются сплошными основными линиями, которые начинаются соответственно в перспективах и вторичных проекциях конечных точек прямой и выполняются как расходящиеся в противоположные стороны отрезки, лежащими соответственно на линиях А∕В∕ и А∕1В∕1 (см. рис. 79). Правомочность данного утверждения доказывается построением перспектив и вторичных проекций точек K и L, лежащих на прямой АВ (обратная задача). При этом соответственно точки А∕ и В∕ , и А∕1 и В∕1 между собой соединяются сплошной тонкой линией вспомогательных построений.

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
Параллельные прямые
Перспективы параллельных прямых пересекаются. Точка пересечения связки параллельных прямых называется точкой схода ( см. точку F/ на
рис. 80).
Точка схода горизонтальных параллельных прямых лежит на линии горизонта (рис.81, а).
Если горизонтальные параллельные прямые перпендикулярны к плоскости картины (П/), то точкой схода их служит главная точка картины (Р) (рис.81, б).
Точка схода параллельных прямых, лежащих в предметной плоскости П1,


Рис. 81. Положения точки схода горизонтальных параллельных прямых:
а – прямые расположены параллельно предметной плоскости П1;
б – прямые перпендикулярны плоскости картины П⁄;
в – прямые лежат в предметной плоскости П1.
Рис. 82. Положение проекций параллельных прямых, параллельных плоскости картины П⁄:
а - прямые перпендикулярны предметной плоскости П1;
б – прямые расположены под углом к предметной плоскости П1;
в - прямые параллельны предметной плоскости П1.

находится на линии горизонта (рис.81, в).
Перспективы и вторичные проекции параллельных прямых параллельны, если прямые параллельны плоскости картины (П/) (рис.82).
Пересекающиеся и скрещивающиеся прямые
Если две прямые имеют общую точку, то точки пересечения их перспектив и вторичных проекций на плоскости картины должны лежать на общем перпендикуляре к линии горизонта (h – h), а прямые являются пересекающимися
(рис.83, а).
Если прямые не имеют общей точки, а их перспективы и вторичные проекции пересекаются, то такие прямые являются скрещивающимися (рис.83, б).

ВЫБОР ТОЧКИ И УГЛА ЗРЕНИЯ. ОРИЕНТИРОВКА КАРТИНЫ
Для того, чтобы обеспечить удачное перспективное изображение предмета, рекомендуется руководствоваться следующими правилами, выработанными практикой.
У
 гол между проецирующими лучами, направленными в крайние точки плана предмета –
гол между проецирующими лучами, направленными в крайние точки плана предмета –
угол зрения «f» (рис. 84) должен составлять от 180 до 530. Оптимальное значение угла зрения равно 280. Если вертикальные размеры
предмета больше его длины, то точку зрения S следует перенести от картины П/ на полторы – две высоты предмета, чтобы угол зрения в вертикальной плоскости оказался в допустимых размерах, рекомендованных для угла «f».
2. Картинную плоскость П/ ориентируют так, чтобы:
а) главная Р точка оказалась в пределах средней трети угла зренияf;
б) горизонтальный след П/1 картинной плоскости с одной из сторон плана
предмета составлял от 25 до 30 градусов.
Боковой фасад при этом получит сильное перспективное сокращение. Целесообразно кроме того, картинную плоскость совместить с одним из ребер предмета, которое на перспективной проекции изобразится в истинном размере.
3. Высоту горизонта обычно принимают на уровне глаз человека, стоящего на земле, т.е. Н = 1,5 ÷ 1,7 м. При изображении застройки большого района высоту горизонта берут равной Н = 100 м и более. Такая перспектива называется перспективой с птичьего полета.
МЕТОДЫ ПОСТРОЕНИЯ ПЕРСПЕКТИВЫ
РАДИАЛЬНЫЙ МЕТОД
Сущность этого метода заключается в определении точек пересечения лучей с картинной плоскостью (рис. 85).
Перспектива А/ и вторичная проекция А/1 точки А на плоскости картины П/ строятся на координатах ZA, ZA1 и ℓA. Координаты ZA и ZA1 – это высотные отметки (расстояние от предметной плоскости) фронтальных проекций (А/)2 и (А/1)2 точек пересечения проекционных лучей S2А2 и S2(А1)2 из точки зрения S на точку А и ее горизонтальную проекцию А1 с плоскостью картины. Координата ℓA – это расстояние на плане (в предметной плоскости) между линией РР0 и проекцией линии пересечения лучевой плоскости на точку А с плоскостью картины.

МЕТОД АРХИТЕКТОРОВ
Данный метод построения перспективы основан на использовании точек схода параллельных прямых.
Сущность рассматриваемого метода может быть показана на примере построения перспективы фигуры, расположенной на горизонтальной плоскости
(рис. 86):
-
строится план фигуры (например, план фасада здания); -
с учетом вышеуказанных рекомендаций определяются положения следа картинной плоскости П∕1, точки зрения S (S1, S2) и главной точки P (P1 ≡ P0) на плане; -
л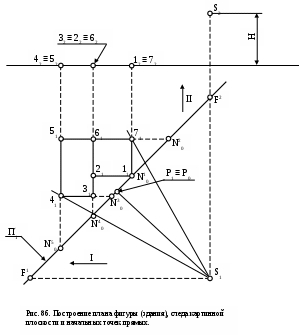 инии контура плана могут быть разделены на два пучка параллельных пря-
инии контура плана могут быть разделены на два пучка параллельных пря-
мых (направления Iи II). Определяются перспективы несобственных точек (F11иF12) каждого из пучков. ТочкаF11 является перспективой несобственной точки пучка параллельных прямых направления I, а точкаF12 является перспективой несобственной точки пучка параллельных прямых направления II. Обе точки найдены при помощи лучей S1F11 и S1F12, параллельных соответственно направлениям Iи II;
-
в качестве вторых точек для построения перспективы каждой из прямых используются характерные точки, в которых эти прямые пересекают плоскость картины, т.е. начальные точки прямых ( точкиN10,N20,N30,N40,N50,); -
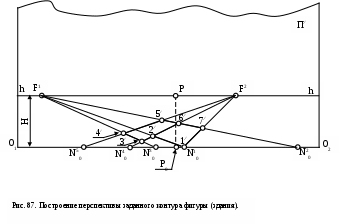
полученные точки с плана (рис. 86) с учетом масштаба построения перспективы переносятся на картину (рис. 87). При этом точки F1 ,F2 и Р откладываются на линии горизонта (h - h), а точкиN10,N20,N30,N40,N50 на линию основания картины (О1 – О2). Расстояние между линией горизонта (h - h) и линией основания картины (О1 – О2) принимается равным высоте расположения точки зрения S– H (с учетом масштаба). Строятся перспективы прямых, пересечения которых определяют вершины заданного контура. Так, точка пересечения прямых N30F1 и N40F2 представляют собой перспективу точки 3. Аналогично находятся остальные точки. -