Файл: Курс лекций санктпетербург 2002 Министерство образования рф.doc

Область применения той или иной системы изображений зависит, прежде всего, от целей, которые ставятся при построении чертежа. Из представленных в таблице систем наиболее широкое применение в техническом проектировании имеет эпюр (ортогональный чертеж). На их основе выполняются рабочие и сборочные чертежи, эскизы деталей, схемы и т.д. Поэтому в дальнейшем изложении курса основное внимание будет уделено именно этому методу построения.

Однако, и другие методы проецирования находят применение в горно-геологических работах, поэтому в лекциях будут рассмотрены также основные правила изображения предметов при помощи линейной перспективы и аксонометрической проекции.

ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ. ПРОЕЦИРОВАНИЕ ТОЧКИ

Любой предмет пространства может рассматриваться как определенная совокупность отдельных точек этого пространства. Поэтому для изображения различных предметов пространства необходимо научиться строить изображения отдельной точки пространства.

Таким образом, изучение метода построения ортогонального чертежа начнем с изучения проецирования точки.

Представим в пространстве три взаимно перпендикулярные плоскости (рис. 6, а):

₁ - горизонтальную плоскость проекций;

₂ - фронтальную плоскость проекций;

₃ - профильную плоскость проекций.

Для наглядного изображения плоскостей проекций взята так называемая кабинетная проекция¹, известная из курсов геометрии и черчения средней школы.

Плоскости проекций пересекаются по прямым, которые называются осями проекций и обозначаются x, y и z. Точка О – точка пересечения всех трех осей проекций – называется началом координат.


Рис. 6


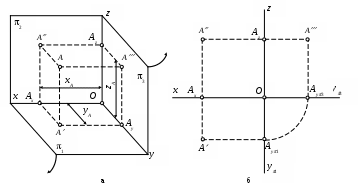
Представим себе также в пространстве некоторую точку А. Для того, чтобы получить проекцию точки A на горизонтальную плоскость проекций ₁, необходимо провести через эту точку прямую, перпендикулярную плоскости ₁, и найти точку пересечения A этой прямой с плоскостью ₁. Точка A называется горизонтальной проекцией точки A. Путем ортогонального проецирования точки A на фронтальную 

---

₂ и профильную ₃ плоскости проекций образуются ее фронтальная и профильная проекции (соответственно точки A и A).

Длины отрезков, измеряемые некоторой установленной единицей длины и равные расстояниям от точки А до горизонтальной ₁, фронтальной ₂ и профильной ₃ плоскостей проекций, называются прямоугольными (декартовыми) координатами:

• 
  по оси x - абсцисса, равная отрезку x_A=AA;
  
• 
  по оси y - ордината, равная отрезку y_A=AA;
  
• 
  по оси z - аппликата, равная отрезку z_A=AA.
  

Три координаты точки однозначно определяют ее положение в пространстве.

Взаимно перпендикулярные плоскости, изображенные на рис. 6, дают нам пространственный чертеж. Для получения всех трех проекций точки в одной плоскости чертежа все три плоскости проекций ₁, ₂ и ₃ условно совмещают с плоскостью чертежа. Это совмещение выполняется следующим образом.

Фронтальная плоскость проекций ₂ принимается за плоскость чертежа, горизонтальная плоскость проекций ₁ совмещается с плоскостью чертежа вращением вокруг оси x, а профильная плоскость проекций ₃ - вращением вокруг оси z. Направление вращения на рис. 6, а показано стрелками.

При совмещении плоскости ₁ с плоскостью чертежа положительное направление оси y совмещается с отрицательным направлением оси z, а отрицательное направление – с положительным направлением оси z. На чертеже изображение этой оси y принято обозначать y_1 (рис. 6, б).

При совмещении плоскости ₃ с плоскостью чертежа положительное направление оси y совмещается с отрицательным направлением оси x, а отрицательное направление – с положительным направлением оси x. На чертеже изображение этой оси y принято обозначать y_3.

В результате образуется ортогональный чертеж или эпюр (от франц. epure - чертеж, проект). На эпюре изображаются только проекции геометрических объектов, а не сами объекты.

Любые две проекции точки, изображенные на эпюре, связаны между собой линией проекционной связи, перпендикулярной оси проекций (на чертеже она обозначается штриховой линией):

• 
  горизонтальная и фронтальная проекции (точки А и А) расположены на линии проекционной связи, перпендикулярной оси x;
  
• 
  фронтальная и профильная проекции (точки А и А) - на линии проекционной связи, перпендикулярной оси z;
  
• 
  горизонтальная и профильная проекции (точки А и А) - на линии проекционной связи, перпендикулярной оси y.
  

---

Вследствие того, что отрезки ОА_y1и OА_y3 являются изображением одной и той же координаты y_A, точки А_y1и А_y3 связывают дугой окружности с центром в начале координат.

Каждая проекция точки А определяется двумя координатами:

• 
  горизонтальная проекция А(x_A; y_A);
  
• 
  фронтальная проекция А (x_A; z_A);
  
• 
  профильная проекция А (y_A; z_A).
  

Положение точки А может быть задано как графически, так и аналитически. Пример графического изображения точки А рассмотрен нами на рис. 6. Аналитическая форма задания точки представляет собой числовое выражение трех координат точки А, измеряемое в выбранных единицах длины (например, запись А (3;2;3) означает, что x_A =3, y_A =2, z_A =3).

От аналитической формы задания точки легко перейти к графическому изображению этой точки на ортогональном чертеже.
П 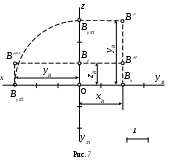ример 1. Построить проекции точки

В (-2;-3;1).
1. Выбираем единичный отрезок (рис.7).

2. С учетом знака откладываем на осях проекций координатные отрезки

x_В = ОВ_х = -2;

y_В = ОВ_y1 = ОВ_y3 = -3;

z_В = ОВ_z = 1.

3. Отмечаем точки В_x, В_y1, В_y3, В_z.

4. Из построенных точек В_x, В_y1, В_y3, В_z проводим линии проекционной связи, перпендикулярные осям проекций, и на их пересечениях отмечаем проекции точки В:

В = (В_xВ  x)  (В_y1В  y_1);

В = (В_xВ  x)  (В_zВ  z);

В = (В_y3В  y_3)  (В_zВ  z).
Две проекции точки, построенные на эпюре, однозначно определяют ее положение в пространстве. По двум проекциям заданной точки можно построить третью, и притом только одну.




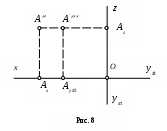
Пример 2. Построение третьей проекции точки по двум заданным.

---

1. 
   Даны фронтальная и профильная проекции точки А (рис. 8):
   

– фронтальная проекция А определяется координатами x_А = ОА_x, z_А = ОА_z, А = (А_xА  x)  (А_zА  z);

- профильная проекция А определяется координатами y_А = ОА_y3, z_A = ОА_z, А = (А_y3А  y_3)  (А_zА  z).

2. Из имеющихся проекций проводим линии проекционной связи, перпендикулярные осям проекций и определяем координатные отрезки ОА_x, ОА_y, ОА_z, равные соответствующим координатам точки А:

ОА_x = x_А, ОА_y= y_А, ОА_z= z_А.

3. На пересечении линий проекционной связи с осями проекций отмечаем точки А_x, А_y3, А_z.

4. Строим третью, горизонтальную проекцию точки А – А (рис. 9). Горизонтальная проекция А определяется координатами:

x_А = ОА_x, y_А = ОА_y1, А = (А_xА  x)  (А_y1А  y_1).

П 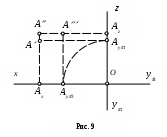ри определении точки А_у1 по А_у3 перенос осуществляется с оси у_3 на соответствующее по знаку направление оси у_1 .
В зависимости от расположения точки относительно плоскостей проекций различают:

1) точки общего положения, не принадлежащие плоскостям проекций (например, точка А на рис. 6);

2) точки частного положения, лежащие в плоскостях проекций ₁, ₂, ₃, на осях проекций x, y, z или в начале координат.

У точки общего положения все три координаты отличны от нуля.

Если точка лежит в плоскости проекций, то одна из ее координат равна нулю, по оси, перпендикулярной этой плоскости проекций.

Если точка лежит на оси проекций, то две другие ее координаты равны нулю.

Е
сли все три координаты точки равны нулю, то точка лежит в начале координат.

---

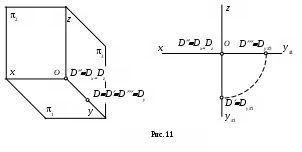
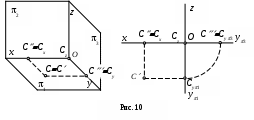
На рис. 10 изображена точка С, принадлежащая горизонтальной плоскости проекций, а на рис. 11 - точка D, лежащая на оси y.

---