ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 86
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. Все системы параметровкоэффициентов описывают один и тот же четырехполюсник, поэтому между различными системами параметровкоэффициентов существует однозначная взаимосвязь.
Пример. Установим связь между апараметрами и Z-параметрами. Решая систему уравнений в Z-параметрах (12.3) относительно неизвестных U1 и I1, находим:
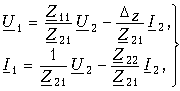
где DZ = Z11Z22 - Z12Z21 - определитель системы уравнений (12.3).
Сравнивая эту систему уравнений с системой (12.4), устанавливаем, что A11 = Z11/Z22; A12 = -DZ/Z21; A21 = 1/Z21 и A22 = -Z22/Z21. Решая систему (12.4) относительно неизвестных U1 и U2, можно найти выражение Z-параметров через апараметры:
где DA = A11A22 - A12A21 - определитель системы уравнений (12.4).
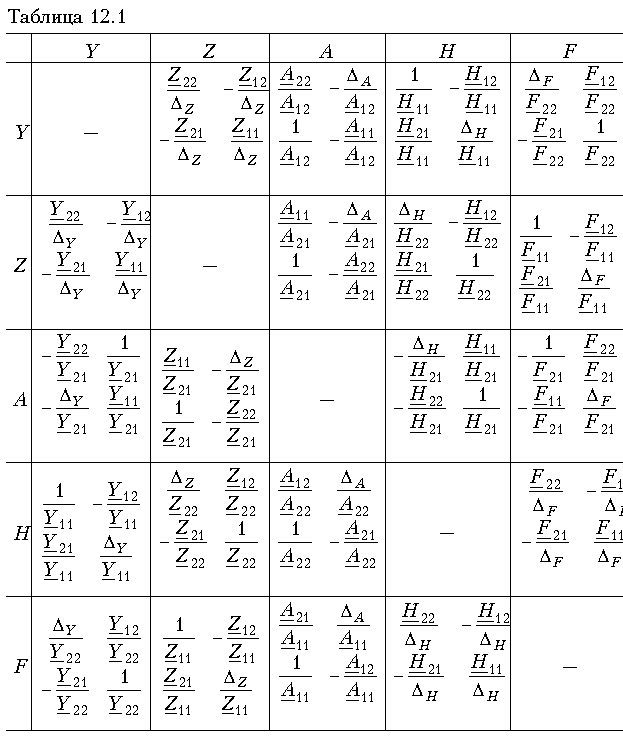
Аналогичным образом можно установить связь между другими системами параметров. В табл. 12.1 приведены соотношения между различными системами параметровкоэффициентов.
3. Пассивный четырехполюсник полностью характеризуется не более чем тремя независимыми параметрами. Действительно, в многоконтурной схеме пассивного четырехполюсника взаимные сопротивления Zkm и Zmk k-го и m-го контуров равны между собой. Следовательно, Y12 = -Y21. Зная связь между Y-параметрами и Z-параметрами, можно установить, что Z12 = -Z21. Далее можно показать, что для апараметров справедливо соотношение
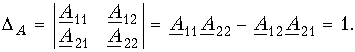
Это легко доказать, если выразить в данном определителе апара-метры, например, через Z-параметры.
Наконец, аналогичным образом можно найти, что H12 = H21 и F12 = F21.
Таким образом, независимыми параметрами четырехполюсника могут быть: Y11, Y12 = -Y21, Y22; Z11, Z12 = -Z21, Z22; H11, H12 = = H21, H22; F11, F12 = F21 и F22 или любые три из параметров A11, A12, A21 и A22.
4. При изменении направления передачи энергии через четырехполюсник во всех выражениях, включающих апараметры, коэффициенты A11 и A22 меняются местами.
Рассмотрим передачу энергии через четырехполюсник в обратном направлении, т. е. от зажимов 2-2' к зажимам 1-1' (рис. 12.3). Если в уравнениях передачи (12.4) заменить напряжение U1 и ток I1 на зажимах 1-1' на напряжение U2' и ток -I2' в соответствии с рис. 12.3, а напряжение U2 и ток I2 на зажимах 2-2' на величины -U1' и -I1', то (12.4) можно переписать в виде
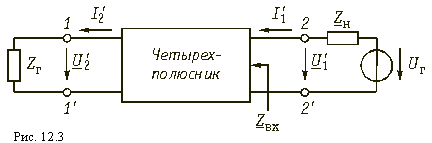
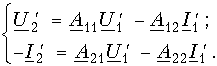
Решая эту систему относительно нового входа четырехполюсника, т. е. относительно переменных U1' и I1', получаем
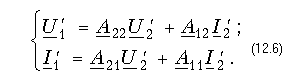
Сопоставляя эти уравнения с (12.4), можно сделать интересное наблюдение: в уравнениях передачи параметры A11 и A22 поменялись местами. Оказывается, этот факт справедлив не только для уравнений передачи, но и для любых других выражений, в которые входят апараметры.
5. Симметричные пассивные четырехполюсники имеют только два независимых параметра. В самом деле, в случае симметричного пассивного четырехполюсника не имеет значения направление передачи энергии: напряжения и токи на входе и выходе не изменяются при замене местами зажимов. Сравнивая уравнения передачи (12.4) и (12.6), устанавливаем, что A11 = A22. Из табл. 12.1 находим также, что в симметричных четырехполюсниках Y11 = = -Y22; Z11 = -Z22 и DH = -1.
Любой симметричный пассивный четырехполюсник полностью описывается двумя независимыми параметрами: A11 = A22 и любым из параметров A12 и A21 (так как они связаны уравнением A11A22 - - A12A21 = 1); Y11 = -Y22 и Y12 = -Y21; Z11 = -Z22 и Z12 = -Z21; H12 = H21 и любым из параметров H11 и H22 (так как для симметричных четырехполюсников H11H22 - H12H21 = -1); F12 = F21 и любым из параметров F11 и F22.
6. Параметрыкоэффициенты имеют определенный физический смысл. Для выявления этого физического смысла следует четырехполюсник поставить в такой режим работы, при котором уравнения передачи содержат лишь один интересующий нас параметр. Подобное произойдет, если использовать режимы холостого хода (XX -размыкания пары зажимов) и короткого замыкания (КЗ - замыкания накоротко пары зажимов). Так, при XX на зажимах 2-2' (см. рис. 12.1) ток I2 = 0. Тогда уравнения передачи, содержащие ток I2, например уравнения (12.3) в Z-параметрах, имеют вид:
Коэффициент Z11 = U1/I1 при I2 = 0 есть входное сопротивление четырехполюсника, измеренное со стороны зажимов 1-1' при разомкнутых зажимах 2-2' или входное сопротивление XX.
Коэффициент - отношение комплексного действующего напряжения на разомкнутых зажимах 2-2' четырехполюсника к комплексному действующему току, протекающему через зажимы 1-1', или взаимное (передаточное) сопротивление XX.
Рассматривая режим XX на зажимах 1-1' (I1 = 0), убеждаемся из уравнений (12.3), что Z22 - выходное сопротивление четырехполюсника при разомкнутых входных зажимах, a Z12 - взаимное (передаточное) сопротивление при XX на зажимах 1-1'.
Предлагаем читателю самостоятельно установить физический смысл остальных параметров, "устраивая" поочередно XX на зажимах 2-2' (I2 = 0) и зажимах 1-1' (I1 = 0) и КЗ на этих же зажимах (U2 = 0 и U1 = 0) и используя соответствующие уравнения передачи (12.2), (12.4) и (12.5).
7. Из предыдущего свойства следует, что параметрыкоэффициенты являются комплексными величинами, так как они определяются отношением комплексных амплитуд (действующих значений) напряжений и токов. В случае анализа четырехполюсника в режиме негармонических колебаний используют спектральные представления электрических величин. Можно показать, что параметрыкоэффициенты, рассматриваемые относительно не отдельной частоты, а определенного спектра частот, являются рациональными функциями оператора jw. При переходе от оператора jw к оператору р параметрыкоэффициенты представляют собой рациональные функции оператора р.
Пример. Для четырехполюсника на рис. 12.2, б определим параметр Z11. Исходя из физического смысла параметра Z11 (он является входным сопротивлением гобразной схемы при разомкнутых зажимах на выходе), определяем из рис. 12.2, б: Z11 = Z1 + Z2.
Этот же результат можно получить следующим образом:
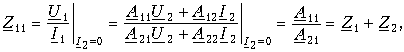
где значения параметров A11 и A21 взяты из первого примера этой главы.
Пусть далее двухполюсник Z1 состоит только из индуктивности L, а двухполюсник Z2 - только из емкости С. Тогда, используя операторную форму записи, получаем
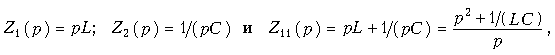
т. е. Z11 является дробнорациональной функцией оператора р с положительными вещественными коэффициентами. Нули этой функции - мнимые и лежат на мнимой оси комплексной плоскости, полюс р1 = 0. При замене оператора р оператором jw переходим к частотной характеристике
Полученные выражения Z11(р) и Z11(jw) напоминают выражение входного сопротивления последовательного LC-контура. Это объясняется тем, что входное сопротивление гобразной цепи (см. рис. 12.2, б) при разомкнутых зажимах определяется последовательным соединением двухполюсников Z1, и Z2 (индуктивности и емкости), т. е. Z11 является сопротивлением двухполюсника (ср. с (4.115)).

12.3. Применение матриц к расчету четырехполюсников
Уравнения передачи в матричной форме. Любую из систем уравнений передачи четырехполюсника можно записать в матричной форме. В частности, для системы уравнений в Y-параметрах (12.2)
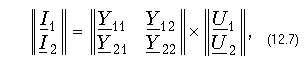
где слева и справа записаны матрицы-столбцы.
Действительно, выполняя операцию умножения в правой части (12.7), имеем
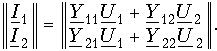
Из равенства этих матриц следует система уравнений (12.2). Система уравнений в Z-параметрах в матричной форме записи имеет вид:
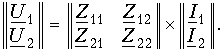
Для уравнений передачи в апараметрах
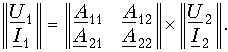
Наконец, запишем в матричной форме системы уравнений передачи в нпараметрах и F-параметрах:
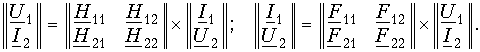
Расчет соединений четырехполюсников. Сложные четырехполюсники можно представить в виде различных соединений простых четырехполюсников. При этом параметры сложного четырехполюсника могут быть найдены по параметрам образующих его простых четырехполюсников.
На рис. 12.4 показана схема каскадного соединения двух четырехполюсников. В соответствии с обозначениями на рисунке при каскадном соединении U2'=U1'' I2'=I1''. Для каждого из четырехполюсников можно составить матричные равенства:
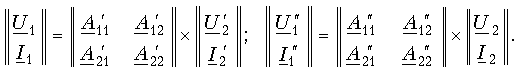
Так как матрицы
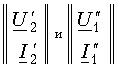
равны между собой, получаем для результирующего четырехполюсника.
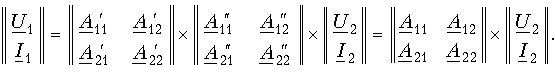
Таким образом, матрица А результирующего четырехполюсника при каскадном соединении равна произведению одноименных матриц соединенных четырехполюсников: А = А'А''. Это правило распространяется на любое число каскадно соединенных четырехполюсников, причем матрицы должны записываться в порядке следования четырехполюсников, так как умножение матриц не подчиняется переместительному закону.