Файл: Руководство к лабораторным работам по дисциплине Теория управления для студентов по направлению Т. 02 Автоматика и управление в технических системах.doc

ЛАБОРАТОРНАЯ РАБОТА 2

Исследование временных характеристик простейших объектов и объектов первого порядка
Цель работы: изучение временных характеристик звеньев 1-го порядка на MATLAB SIMULINK.


Краткие теоретические сведения

Временные характеристики

1) Импульсная или весовая функция звена w(t). Импульсная или весовая функция представляет собой реакцию звена на единичную импульсную функцию.

Единичной импульсной функцией или -функцией называется функция, равная нулю всюду, кроме начала координат, но притом так, что интеграл от нее по любому интервалу, содержащему нуль, равен единице, т.е.



Кроме того, при любом >0.

Иначе говоря, весовая функция w(t) представляет собой переходный процесс на выходе звена (рис.8) при подаче на его вход единичного импульса.


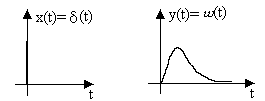
Рис.8. Временные диаграммы входного и выходного

сигналов звена
2) Переходная функция звена h(t). Переходная функция представляет собой реакцию звена на единичную ступенчатую функцию, удовлетворяющую условию



Как видим (рис.9), переходная функция является переходным процессом на выходе звена при единичном скачке на его входе.


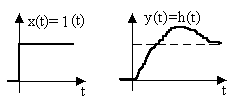
Рис.9. Временные диаграммы входного и выходного
сигналов звена
Простейшие объекты и объекты 1-го порядка

1) Безынерционное (идеальное усилительное) звено. Это звено не только в статике, но и в динамике описывается алгебраическим уравнением

y(t) = kx(t).

Передаточная функция:

---

W(s) = k.

Переходная и импульсная функции:

h(t) = k1(t), w(t) = kδ (t).

2) Идеальное интегрирующее звено. Уравнение и передаточная функция имеют вид

py(t) = x(t), .

Переходная и импульсная функции:

h(t) = t, w(t) = 1(t).

3) Идеальное дифференцирующее звено. Уравнение и передаточная функция имеют вид

y(t) = px(t), W(s) = s .

Переходная и импульсная функции:

h(t) =δ (t), w(t) = .

4) Апериодическое (инерционное) звено первого порядка. Уравнение и передаточная функция звена:

(Tp+1) y(t) = x(t), ,

где T - постоянная времени, характеризует степень инерционности звена, т.е. длительность переходного процесса.

Переходная и импульсная функции:

.

5) Форсирующее (дифференцирующее) звено первого порядка. Дифференциальное уравнение и передаточная функция

y(t) = (τp+1) x(t) , W(s) = τs+1,

где τ- постоянная времени дифференцирования.

Переходная и импульсная функции:

h(t) = 1(t) + τ δ (t), w(t) = δ(t) +τ.
Задание и порядок выполнения лабораторной работы

1. Соберите модели следующих звеньев:

• 
  усилительное звено;
  
• 
  интегрирующее звено;
  
• 
  дифференцирующее звено;
  
• 
  апериодическое звено первого порядка;
  
• 
  форсирующее звено первого порядка.
  

2. Составьте схемы моделирования, для каждого звена подставляя значения соответствующие варианту (табл.2).

3. Подавая единичный ступенчатый сигнал на каждый из объектов, перечисленных в п.1, получите выходные характеристики.

4. Аналогично п.3 получить выходные характеристики с использованием единичного импульсного сигнала.
Таблица 2

№	k	Т	№	k	Т
1	5	1.0	11	9.1	0.11
2	0.5	0.7	12	6.9	0.05
3	1.2	0.55	13	2.2	0.47
4	4.7	0.64	14	4.4	0.59
5	8.3	0.91	15	2.8	0.63
6	5.9	0.63	16	3.7	0.03
7	1.1	0.2	17	6.4	0.19
8	6.3	0.75	18	5.5	0.55
9	3	0.32	19	9.9	0.48
10	1.9	0.89	20	10	0.36

---

Контрольные вопросы:

1. Что называется передаточной функцией? Как ее получить, если известно дифференциальное уравнение СУ?

2. Какие Вам известны временные характеристики? Дайте определение этих характеристик.

3. Какими аналитическими выражениями связана передаточная функция СУ с переходным процессом и функцией веса?

4. Запишите дифференциальные уравнения и уравнения временных характеристик для следующих звеньев:

• 
  апериодического 1-го порядка;
  
• 
  форсирующего 1-го порядка;
  
• 
  интегрирующего;
  
• 
  дифференцирующего;
  
• 
  пропорционального.
  

5. Как по графику переходного процесса пропорционального, ин­тегрального и апериодического 1-го порядка, определить коэффици­ент передачи и постоянные времени соответствующей передаточной функции?

6. Временные характеристики объектов управления?
ЛАБОРАТОРНАЯ РАБОТА 3

Исследование временных характеристик объектов

второго порядка
Цель работы: изучение временных характеристик динамических звеньев второго порядка на MATLAB SIMULINK.
Краткие теоретические сведения: звенья 2-го порядка описываются дифференциальными уравнениями 2-го порядка и входят в класс линейных систем.

Обычно рассматривают 3 типовых звена 2-го порядка: колебательное, консервативное и апериодическое звено 2-го порядка.

Объекты 2-го порядка

1) Апериодическое (инерционное) звено второго порядка. Дифференциальное уравнение звена имеет вид

,

причем предполагается, что 2Т₂≥ Т₁ ( - другое логическое условие [см. ниже]).

Передаточная функция звена

.

Из выражения следует, что апериодическое звено второго порядка можно рассматривать как комбинацию двух апериодических звеньев первого порядка.

2) Колебательное звено. Описывается дифференциальным уравнением

---

,

при Т₁>2T₂ корни характеристического уравнения комплексные и уравнение переписывают в виде

(T₁²p²+2ξT₁p+1) y(t) =kx(t),

где Т₁ - постоянная времени, определяющая угловую частоту свободных колебаний λ=1/Т; - параметр затухания, лежащий в пределах 0<ξ<1.

Общепринятая запись передаточной функции колебательного звена имеет вид



3) Консервативное звено. Консервативное звено является частным случаем колебательного звена при ξ=0. Тогда передаточная функция консервативного звена будет иметь вид . Оно представляет собой идеализированный случай, когда можно пренебречь влиянием рассеяния энергии в звене.

Временные характеристики соответствуют незатухающим колебаниям с угловой частотой 1/T.
Задание и порядок выполнения лабораторной работы

1. Составьте передаточные функции следующих звеньев:

а) колебательное звено второго порядка;

б) апериодическое звено второго порядка;

в) консервативное звено второго порядка.

2. Постройте схемы моделирования, для каждого звена подставляя значения коэффициента усиления k и постоянные времени Т₁, Т₂, соответствующие варианту (табл. 3).

3. Подавая ступенчатую функцию на каждый из объектов, исследуйте выходные характеристики.

4. Аналогично п.3 получить выходные характеристики с использованием импульсной функции.
Таблица 3

№	k	Т1	Т2	№	k	Т1	Т2
1	5	0.36	1.0	11	9.1	0.89	0.11
2	0.5	0.48	0.7	12	6.9	0.32	0.05
3	1.2	0.55	0.55	13	2.2	0.75	0.47
4	4.7	0.19	0.64	14	4.4	1	0.59
5	8.3	0.03	0.91	15	2.8	0.2	0.63
6	5.9	0.63	0.63	16	3.7	0.91	0.03
7	1.1	0.59	0.2	17	6.4	0.64	0.19
8	6.3	0.47	0.75	18	5.5	2	0.55
9	3	0.05	0.32	19	9.9	0.55	0.48
10	1.9	0.11	0.89	20	10	0.7	0.36

---

Контрольные вопросы:

1. Запишите передаточные функции и уравнения для следующих звеньев: апериодического 2-го порядка, колебательного, форсирующего и консервативного.

2. Чем отличается апериодическое звено 2-го порядка от колебательного звена?

3. Временные характеристики объектов 2-го порядка.

4. Проведите анализ переходных процессов объектов 1-го и 2-го порядков.

---