Файл: Руководство к лабораторным работам по дисциплине Теория управления для студентов по направлению Т. 02 Автоматика и управление в технических системах.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 105
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
W(s), равной произведению передаточных функций отдельных звеньев: 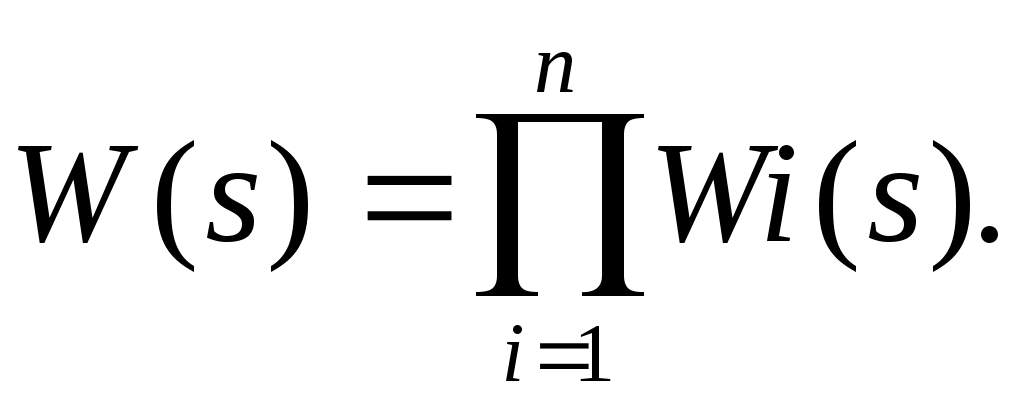
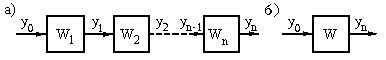
Рис.18
Параллельное соединение звеньев (рис.19, а). При параллельном соединении на вход всех звеньев подается один и тот же сигнал, а выходные величины складываются. Цепь из параллельно соединенных звеньев можно заменить одним звеном (рис.19, б) с передаточной функцией W(s), равной сумме передаточных функций входящих в нее звеньев: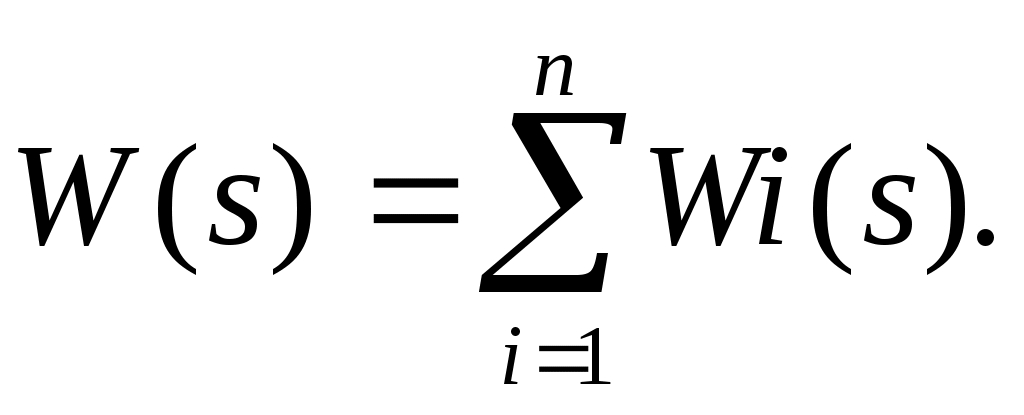
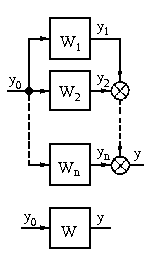
Рис.19
Звено, охваченное обратной связью (рис.20, а). Принято считать, что звено охвачено обратной связью если его выходной сигнал через какое-либо другое звено подается на вход. При этом если сигнал y1 обратной связи вычитается из входного воздействия у0, т. е. е1 = у0- у1, то обратную связь называют отрицательной. Если сигнал у1 обратной связи складывается с входным воздействием уо, т.е. е1=yо+y1, то обратную связь называют положительной.
Разомкнем обратную связь перед сравнивающим звеном (рис.20, а). Тогда получим цепь из двух последовательно соединенных звеньев. Поэтому передаточная функция W разомкнутой цепи (рис.20, а) равна произведению передаточной функции Wп прямой цепи и передаточной функции Wо.с. обратной связи W=Wп*Wо.с. (рис.20, б).
Передаточная функция замкнутой цепи с отрицательной обратной связью - звена, охваченного отрицательной обратной связью, - равна передаточной функции прямой цепи, деленной на единицу плюс передаточная функция разомкнутой цепи:
Wз=Wп/(1+W);
Если обратная связь положительна, то аналогично получим: Wз=Wп/(1+W);
Передаточная функция замкнутой цепи с положительной обратной связью "равна" передаточной функции прямой цепи, деленной на единицу минус передаточная функция разомкнутой цепи. Если передаточная функция
Wo.c=1,то обратная связь называется единичной и структурная схема изображается так, как показано на рис.20, в. Передаточная функция Wз при этом принимает вид Wз=Wп/(1+W) при отрицательной обратной связи и Wз=Wп/(1-W) при положительной обратной связи.
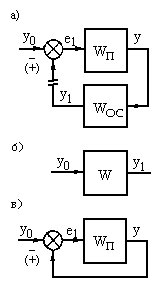
Рис.20
При преобразовании структурных схем возникает необходимость переноса и перестановки сумматоров и узлов.
Задание и порядок выполнения лабораторной работы
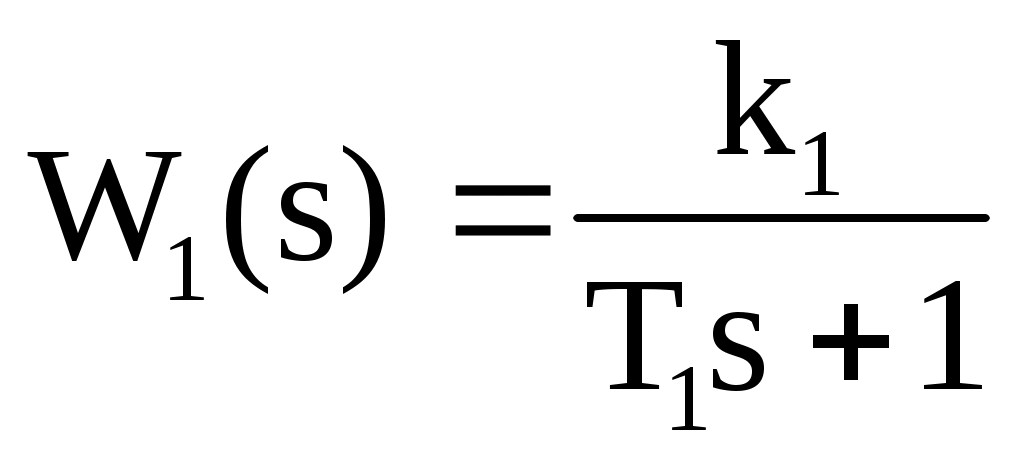
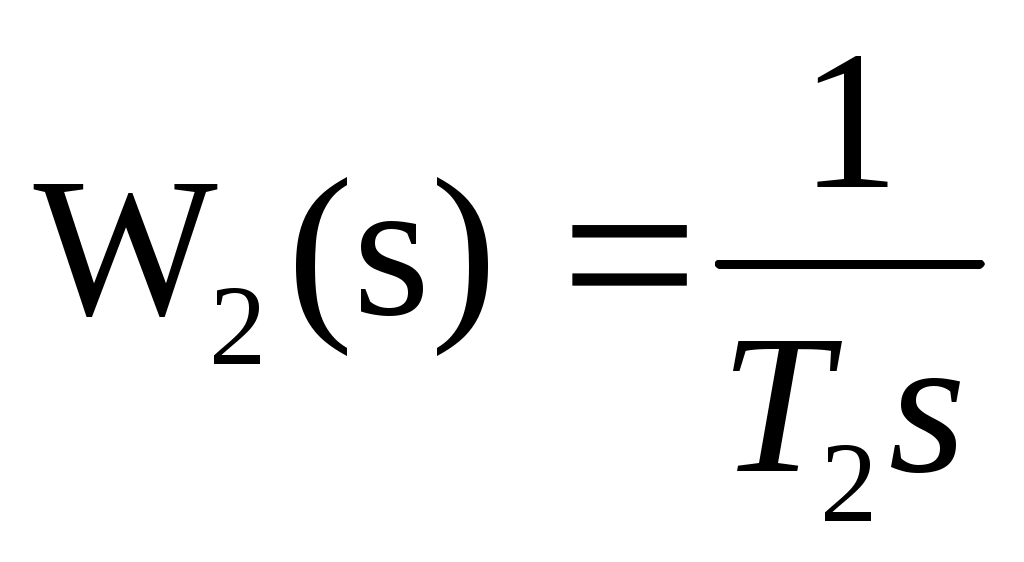
Таблица 5
Контрольные вопросы
ЛАБОРАТОРНАЯ РАБОТА 6
Исследование устойчивости линейных СУ
Цель работы: анализ устойчивости замкнутых систем управления; исследование влияния коэффициентов системы на устойчивость ее переходных процессов.
Краткие теоретические сведения.
Любая система должна быть, прежде всего, работоспособной. Это значит, что она должна нормально функционировать при действии на нее различных внешних возмущений. Иными словами, система должна работать устойчиво.
Понятие устойчивости системы управления связано со способностью возвращаться в состояние равновесия после исчезновения внешних воздействий, которые вывели ее из этого состояния.
Для устойчивости системы необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части, или эти корни на плоскости комплексного переменного были расположены слева от мнимой оси (рис.21).
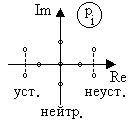
Рис.21. Комплексная плоскость корней
характеристического уравнения
Критерий устойчивости Михайлова.
Критерий устойчивости Михайлова, согласно которому изменение аргумента характеристического вектора определяется по годографу вектора, записанному в виде
D(jw) = X(w) + jY(w) = D(w)ejφ (w) ,
где X(w) и Y(w) действительная и мнимая части характеристического вектора, а D(w) и φ(w) его модуль и аргумент.
Формулировка критерия. Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы изменение аргумента функции D(jw) при изменении w от 0 до ∞ равнялось бы n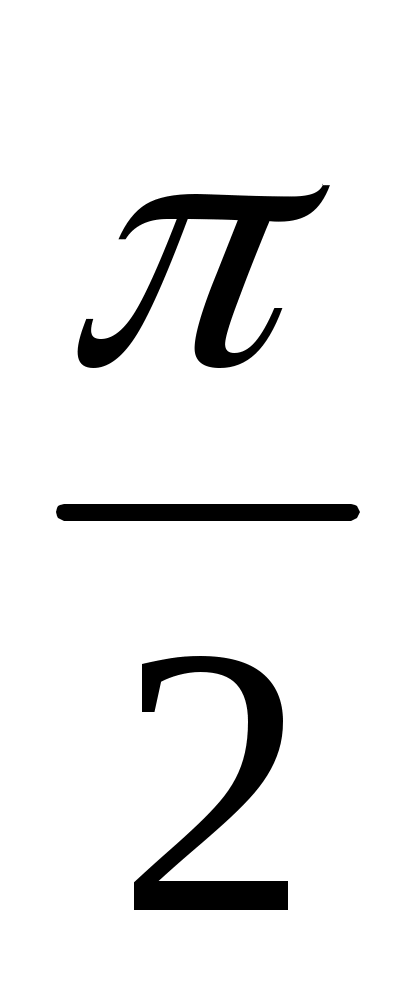 .
.
Другими словами, система устойчива, если годограф характеристического вектора (кривая Михайлова), начинаясь на положительной части действительной оси, обходит последовательно в положительном направлении (против часовой стрелки) n квадрантов, где n - порядок характеристического уравнения системы.
На рис.22 приведены примеры годографов для устойчивой и неустойчивой систем.
Рис.22. Кривая Михайлова:
а - устойчивой системы 3-го порядка; б - неустойчивой системы
Критерий Найквиста. Формулировка критерия.
1. Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы не охватывала точку с координатами (-1, j0).
2. Если разомкнутая система неустойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы охватывала точку с координатами (-1, j0) и при изменении частоты от 0 до ∞ оборачивалась вокруг нее против часовой стрелки m раз, где m - число полюсов разомкнутой системы с положительной вещественной частью.
Рис.23. АФЧХ статических разомкнутых систем
Графики на рис.23,а соответствуют абсолютно устойчивой, нейтральной и неустойчивой системам. Система, АФЧХ разомкнутой цепи которой пересекает вещественную ось только справа от точки с координатами (-1, j0), называется абсолютно устойчивой. В таких системах неустойчивость может наступить только при увеличении общего коэффициента передачи разомкнутой цепи.
Если АФЧХ разомкнутой системы (рис.23,б) пересекает вещественную ось и слева от точки с координатами (-1, j0), но при этом число положительных (сверху вниз) переходов характеристики через ось абсцисс левее точки (-1) равняется числу отрицательных переходов (снизу вверх), то систему называют условно устойчивой. Неустойчивой такая система может быть как при увеличении, так и при уменьшении общего коэффициента передачи разомкнутой цепи.
3. Если передаточная функция разомкнутой системы содержит в своем составе интегрирующие звенья, то АФЧХ начинается в бесконечности ( рис.24).
Рис.24. АФЧХ астатических разомкнутых систем
Графики на рис.24. соответствуют устойчивым системам с первой, второй и третьей степенями астатизма.
Далее приведён пример исследование устойчивости с помощью пакета MATLAB. В командном окне MATLAB задать необходимую передаточную функцию:
» syst=tf(3,[5 1 1])
Transfer function:
3
--------------
5s^2+s+1
В результате в переменную syst будет записан вышеприведенный объект "передаточная функция". Вызов команды Ltiview приведет к загрузке графической системы просмотра линейных систем. На рис. 25 приведен вид окна просмотра для данного примера. В списке рабочих областей (workspace) выбирается одна или несколько исследуемых передаточных функций. Выбирается необходимый тип графика - в данной работе это Nyquist. После обработки в окно просмотра выводится амплитудно-фазовая характеристика разомкнутой системы. Для удобства можно поставить сетку (grid) в меню Plots/Grid On.
Рис.25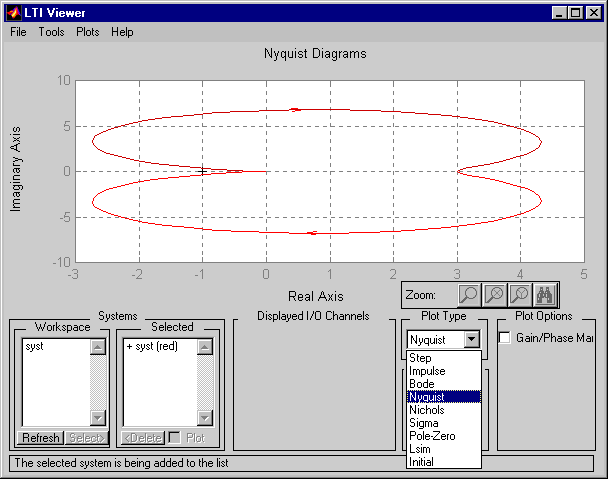
Задание и порядок выполнения лабораторной работы
1. Составьте передаточные функции замкнутых систем по структурным схемам изображенным на рисунках 26,27. Значения коэффициентов усиления и постоянных времени возьмите из табл. 6.
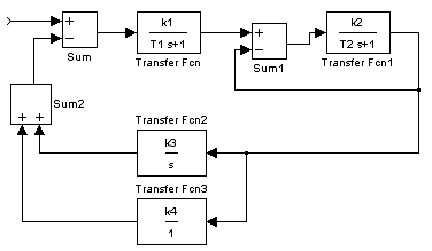
Рис.26
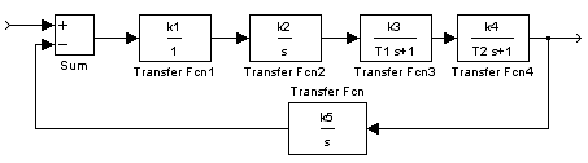
Рис.27.
2. С помощью вышеописанной процедуры исследуйте ЛЧХ И ФЧХ известных передаточных функций. Определите по графикам запас устойчивости по фазе и амплитуде.
3. Выберите из предложенных типов графиков в графической библиотеке Ltiview - график "Nyquest". Зафиксируйте этот график.
4. Повторите п.3 , но выбрав график "Pole- zero" .
5. По предложенным критериям устойчивости и полученным результатам сделайте соответствующие выводы и определите являются ли системы, структурные схемы которых изображены на рис.26,27 устойчивыми.
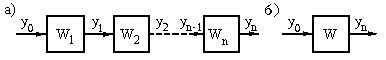
Рис.18
Параллельное соединение звеньев (рис.19, а). При параллельном соединении на вход всех звеньев подается один и тот же сигнал, а выходные величины складываются. Цепь из параллельно соединенных звеньев можно заменить одним звеном (рис.19, б) с передаточной функцией W(s), равной сумме передаточных функций входящих в нее звеньев:

Рис.19
Звено, охваченное обратной связью (рис.20, а). Принято считать, что звено охвачено обратной связью если его выходной сигнал через какое-либо другое звено подается на вход. При этом если сигнал y1 обратной связи вычитается из входного воздействия у0, т. е. е1 = у0- у1, то обратную связь называют отрицательной. Если сигнал у1 обратной связи складывается с входным воздействием уо, т.е. е1=yо+y1, то обратную связь называют положительной.
Разомкнем обратную связь перед сравнивающим звеном (рис.20, а). Тогда получим цепь из двух последовательно соединенных звеньев. Поэтому передаточная функция W разомкнутой цепи (рис.20, а) равна произведению передаточной функции Wп прямой цепи и передаточной функции Wо.с. обратной связи W=Wп*Wо.с. (рис.20, б).
Передаточная функция замкнутой цепи с отрицательной обратной связью - звена, охваченного отрицательной обратной связью, - равна передаточной функции прямой цепи, деленной на единицу плюс передаточная функция разомкнутой цепи:
Wз=Wп/(1+W);
Если обратная связь положительна, то аналогично получим: Wз=Wп/(1+W);
Передаточная функция замкнутой цепи с положительной обратной связью "равна" передаточной функции прямой цепи, деленной на единицу минус передаточная функция разомкнутой цепи. Если передаточная функция
Wo.c=1,то обратная связь называется единичной и структурная схема изображается так, как показано на рис.20, в. Передаточная функция Wз при этом принимает вид Wз=Wп/(1+W) при отрицательной обратной связи и Wз=Wп/(1-W) при положительной обратной связи.

Рис.20
При преобразовании структурных схем возникает необходимость переноса и перестановки сумматоров и узлов.
Задание и порядок выполнения лабораторной работы
-
Заданы апериодическое звено первого порядка и интегрирующее звено.
-
В соответствии с вариантом задания исследовать временные и частотные характеристики каждого звена в отдельности (табл.5). -
Построить схему моделирования с использованием параллельного соединения типовых звеньев. -
Исследовать выходную характеристику схемы моделирования с использованием последовательного соединения типовых звеньев. -
Построить схему моделирования с использованием встречно-параллельного соединения типовых звеньев.
Таблица 5
| № | Т1 | Т2 | k | № | Т1 | Т2 | k |
| 1 | 0.45 | 1.0 | 4 | 11 | 0.51 | 0.11 | 0.2 |
| 2 | 0.56 | 0.93 | 5 | 12 | 0.35 | 1.0 | 8.56 |
| 3 | 0.89 | 0.57 | 89 | 13 | 0.13 | 0.013 | 13 |
| 4 | 0.65 | 0.3 | 4.2 | 14 | 0.46 | 0.19 | 3.79 |
| 5 | 0.7 | 0.67 | 6.67 | 15 | 0.2 | 0.01 | 8 |
| 6 | 0.98 | 0.23 | 9 | 16 | 0.54 | 0.91 | 3.4 |
| 7 | 1.0 | 0.86 | 3.8 | 17 | 1.0 | 0.63 | 6.7 |
| 8 | 0.34 | 0.28 | 5.54 | 18 | 0.3 | 0.44 | 3 |
| 9 | 0.39 | 0.83 | 6.12 | 19 | 0.96 | 0.99 | 8.67 |
| 10 | 0.99 | 0.92 | 90 | 20 | 0.5 | 1.0 | 3.4 |
Контрольные вопросы
-
Что называется структурной схемой ? -
Как условно обозначается звенья в структурной схеме? -
Какие Вы знаете типовые соединения звеньев? -
Для какого типа звена введено понятие разомкнутой и замкнутой СУ? -
Напишите передаточную функцию для каждого типа соединений. -
Какие основные правила преобразования структурных схем Вы знаете? -
Охарактеризуйте вид переходного процесса в СУ, при различных типах соединений.
ЛАБОРАТОРНАЯ РАБОТА 6
Исследование устойчивости линейных СУ
Цель работы: анализ устойчивости замкнутых систем управления; исследование влияния коэффициентов системы на устойчивость ее переходных процессов.
Краткие теоретические сведения.
Любая система должна быть, прежде всего, работоспособной. Это значит, что она должна нормально функционировать при действии на нее различных внешних возмущений. Иными словами, система должна работать устойчиво.
Понятие устойчивости системы управления связано со способностью возвращаться в состояние равновесия после исчезновения внешних воздействий, которые вывели ее из этого состояния.
Для устойчивости системы необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части, или эти корни на плоскости комплексного переменного были расположены слева от мнимой оси (рис.21).

Рис.21. Комплексная плоскость корней
характеристического уравнения
Критерий устойчивости Михайлова.
Критерий устойчивости Михайлова, согласно которому изменение аргумента характеристического вектора определяется по годографу вектора, записанному в виде
D(jw) = X(w) + jY(w) = D(w)ejφ (w) ,
где X(w) и Y(w) действительная и мнимая части характеристического вектора, а D(w) и φ(w) его модуль и аргумент.
Формулировка критерия. Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы изменение аргумента функции D(jw) при изменении w от 0 до ∞ равнялось бы n
Другими словами, система устойчива, если годограф характеристического вектора (кривая Михайлова), начинаясь на положительной части действительной оси, обходит последовательно в положительном направлении (против часовой стрелки) n квадрантов, где n - порядок характеристического уравнения системы.
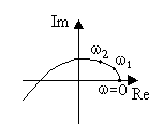
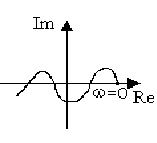
На рис.22 приведены примеры годографов для устойчивой и неустойчивой систем.
 |  |
| а) | б) |
Рис.22. Кривая Михайлова:
а - устойчивой системы 3-го порядка; б - неустойчивой системы
Критерий Найквиста. Формулировка критерия.
1. Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы не охватывала точку с координатами (-1, j0).
2. Если разомкнутая система неустойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы охватывала точку с координатами (-1, j0) и при изменении частоты от 0 до ∞ оборачивалась вокруг нее против часовой стрелки m раз, где m - число полюсов разомкнутой системы с положительной вещественной частью.
 |  |
| а) | б) |
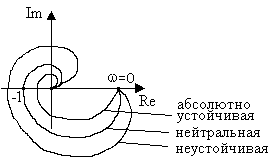
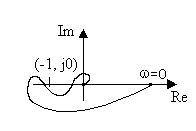
Рис.23. АФЧХ статических разомкнутых систем
Графики на рис.23,а соответствуют абсолютно устойчивой, нейтральной и неустойчивой системам. Система, АФЧХ разомкнутой цепи которой пересекает вещественную ось только справа от точки с координатами (-1, j0), называется абсолютно устойчивой. В таких системах неустойчивость может наступить только при увеличении общего коэффициента передачи разомкнутой цепи.
Если АФЧХ разомкнутой системы (рис.23,б) пересекает вещественную ось и слева от точки с координатами (-1, j0), но при этом число положительных (сверху вниз) переходов характеристики через ось абсцисс левее точки (-1) равняется числу отрицательных переходов (снизу вверх), то систему называют условно устойчивой. Неустойчивой такая система может быть как при увеличении, так и при уменьшении общего коэффициента передачи разомкнутой цепи.
3. Если передаточная функция разомкнутой системы содержит в своем составе интегрирующие звенья, то АФЧХ начинается в бесконечности ( рис.24).
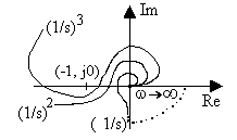 |
Рис.24. АФЧХ астатических разомкнутых систем
Графики на рис.24. соответствуют устойчивым системам с первой, второй и третьей степенями астатизма.
Далее приведён пример исследование устойчивости с помощью пакета MATLAB. В командном окне MATLAB задать необходимую передаточную функцию:
» syst=tf(3,[5 1 1])
Transfer function:
3
--------------
5s^2+s+1
В результате в переменную syst будет записан вышеприведенный объект "передаточная функция". Вызов команды Ltiview приведет к загрузке графической системы просмотра линейных систем. На рис. 25 приведен вид окна просмотра для данного примера. В списке рабочих областей (workspace) выбирается одна или несколько исследуемых передаточных функций. Выбирается необходимый тип графика - в данной работе это Nyquist. После обработки в окно просмотра выводится амплитудно-фазовая характеристика разомкнутой системы. Для удобства можно поставить сетку (grid) в меню Plots/Grid On.
Рис.25

Задание и порядок выполнения лабораторной работы
1. Составьте передаточные функции замкнутых систем по структурным схемам изображенным на рисунках 26,27. Значения коэффициентов усиления и постоянных времени возьмите из табл. 6.

Рис.26

Рис.27.
2. С помощью вышеописанной процедуры исследуйте ЛЧХ И ФЧХ известных передаточных функций. Определите по графикам запас устойчивости по фазе и амплитуде.
3. Выберите из предложенных типов графиков в графической библиотеке Ltiview - график "Nyquest". Зафиксируйте этот график.
4. Повторите п.3 , но выбрав график "Pole- zero" .
5. По предложенным критериям устойчивости и полученным результатам сделайте соответствующие выводы и определите являются ли системы, структурные схемы которых изображены на рис.26,27 устойчивыми.