Файл: Руководство к лабораторным работам по дисциплине Теория управления для студентов по направлению Т. 02 Автоматика и управление в технических системах.doc

2. 
   Для случая идеального двухпозиционного реле, отсутствия коррекции по скорости и нулевого входного сигнала, т.е. при d=0, =0, g=0, задайте начальное отклонение x₁₀ при х₂₀=0 и пронаблюдайте фазовую траекторию, соответствующую свободному движению системы. Коэффициенты передачи интеграторов в модели выбирайте произвольно, исходя из удобства наблюдения изображения. Зарисуйте фазовый портрет системы, а также пронаблюдайте и зафиксируйте процессы х₁(t) и x₂(t).
   
3. 
   В этой же системе введите коррекцию по скорости, полагая 0, и зарисуйте вид фазовых траекторий при =0,25;0,5;1. Каждой из полученных фазовых траекторий поставьте в соответствие процессы х₁(t) и x₂(t). В случае сильной коррекции, приводящей к возникновению скользящего режима, обратите внимание на вид сигнала на выходе релейного элемента. Дайте объяснение полученному результату.
   
4. 
   Что Вы ожидаете получить результат, если обратную связь по скорости выбрать положительной? Проверьте Ваше предположение моделированием.
   
5. 
   Измените, вид релейной характеристики, введя зону нечувствительности, т.е. задайте d0 при m=1. Предскажите вид фазового портрета и проверьте Ваше предположение, моделированием системы, рассматривая свободное движение при отсутствии коррекции по скорости.
   
6. 
   Задайте начальное отклонение х₁₀>d при х₂₀=0 и пронаблюдайте фазовую траекторию при отсутствии коррекции по скорости, изменяя величину зоны нечувствительности.
   
7. 
   Введите коррекцию по скорости, задавая =0,25;0,5;1. Зарисуйте вид процессов х₁(t) и x₂(t) при заданной степени коррекции.
   
8. 
   Реализуйте релейную характеристику гистерезисного типа, задавая d0 и m=-1. При =0 задайте малое начальное отклонение х₁₀<d и пронаблюдайте фазовый портрет и процессы х₁(t) и x₂(t).
   
9. 
   Введите коррекцию по скорости и пронаблюдайте для =0,25;0,5;1 фазовые траектории, соответствующие отработке малых х₁₀<d и больших х₁₀>d начальных отклонений. В чем принципиальное отличие этих траекторий? Как зависят от степени коррекции по скорости параметры предельного цикла и соответствующих ему периодических колебаний?
   
10. 
    Реализуйте релейную характеристику с гистерезисом и зоной нечувствительности, задавая d0 и 0<m<1.
    
11. 
    При =0 задайте начальное отклонение и пронаблюдайте фазовый портрет и соответствующие ему процессы х₁(t) и x₂(t).
    
12. 
    Введите коррекцию по скорости, задайте начальное отклонение х₁₀>d и для различных , исследуйте вид фазовой траектории. Зарисуйте фазовые портреты и процессы х₁(t) и x₂(t).
    

---

Вторая часть

13. 
    По результатам пп.1-12 сделайте выводы о динамических свойствах системы управления объектом с передаточной функцией .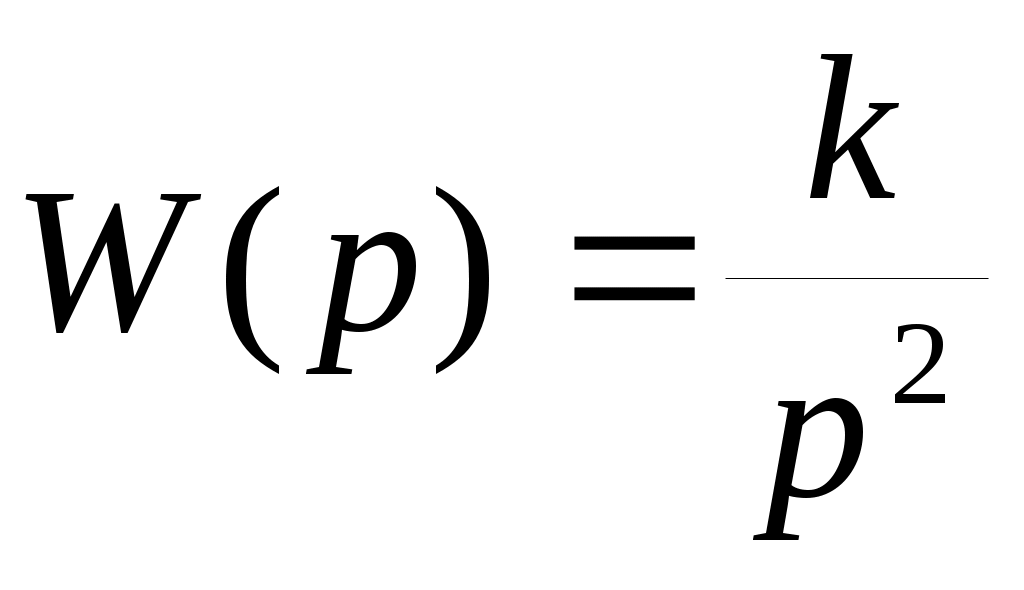
    
14. 
    В системе управления со структурной схемой (рис.34) реализуйте идеальное двухпозиционное реле, задавая W₀(p) линейной части передаточной функцией вида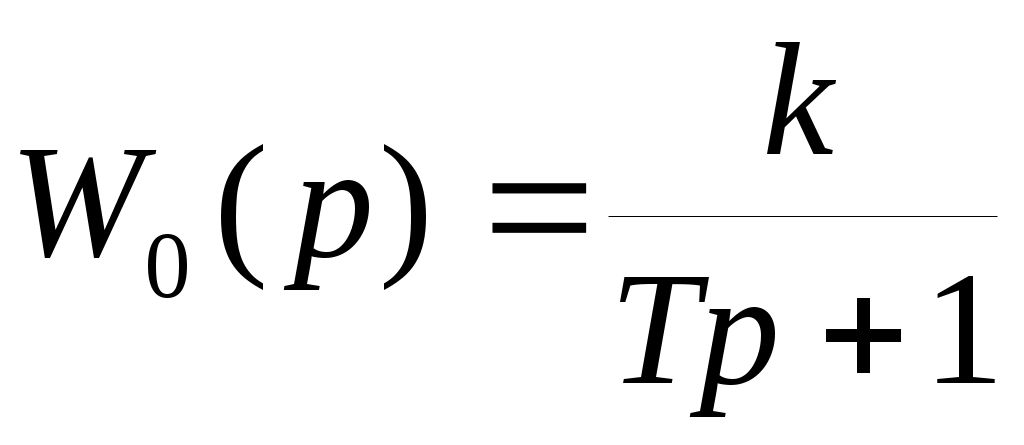 . Значения коэффиента передачи (k) и постоянной времени (Т) возьмите из табл.9.
    
15. 
    Задайте начальное отклонение х₁₀, при х₂₀=0 и пронаблюдайте фазовую траекторию и процессы х₁(t) и x₂(t) при отсутствии коррекции по скорости.
    
16. 
    К чему приводит введение обратной связи по скорости? Что произойдет, если знак обратной связи по скорости выбран неправильно? Ваши ответы проверьте моделированием. Пронаблюдайте и зафиксируйте соответствующие фазовые портреты и процессы х₁(t) и x₂(t).
    
17. 
    В релейной характеристике введите зону нечувствительности, т.е. задавая d0 при m=1.
    
18. 
    Задавая различные начальные отклонения, удовлетворяющие условию х₁₀>d , пронаблюдайте фазовые траектории при отсутствии коррекции по скорости.
    
19. 
    Введите коррекцию по скорости и исследуйте ее влияние на динамику системы при одних и тех же начальных отклонениях х₁₀>d.
    
20. 
    Реализуйте релейную характеристику гистерезисного вида, задавая d0 при m=-1.
    
21. 
    Пронаблюдайте фазовые траектории и процессы х₁(t) и x₂(t) при отработке малых х₁₀<d и больших х₁₀>d начальных отклонений, изменяя величину коррекции по скорости и начиная со значения =0.
    
22. 
    Реализуйте релейную характеристику с гистерезисом и зоной нечувствительности, задавая d0 и 0<m<1.
    
23. 
    Задайте начальное отклонение х₁₀>d и пронаблюдайте фазовые траектории, а также процессы х₁(t) и x₂(t) при различной степени коррекции по скорости. Полученные результаты зафиксируйте.
    

Третья часть

24. 
    По результатам пп.13-23 сделайте выводы о динамических свойствах системы управления объектом с передаточной функцией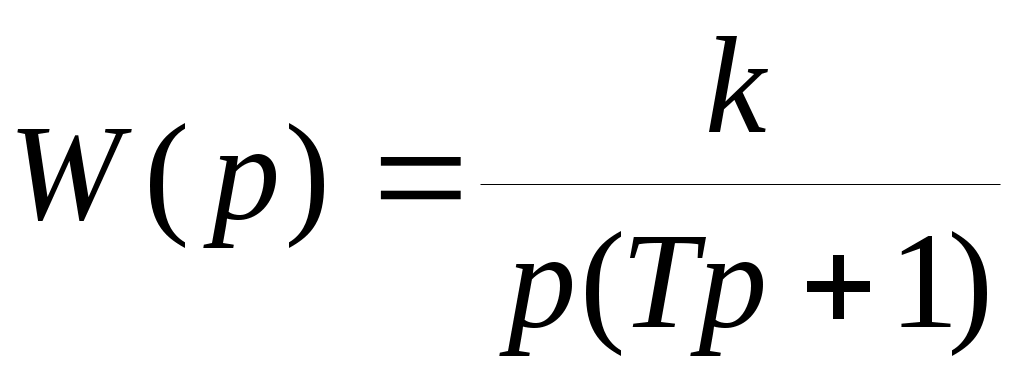 . Значения коэффиента передачи (k) и постоянной времени (Т) возьмите из табл.9.
    
25. 
    В системе управления со структурной схемой (рис.34) реализуйте идеальное двухпозиционное реле, задавая W₀(p) линейной части передаточной функцией вида .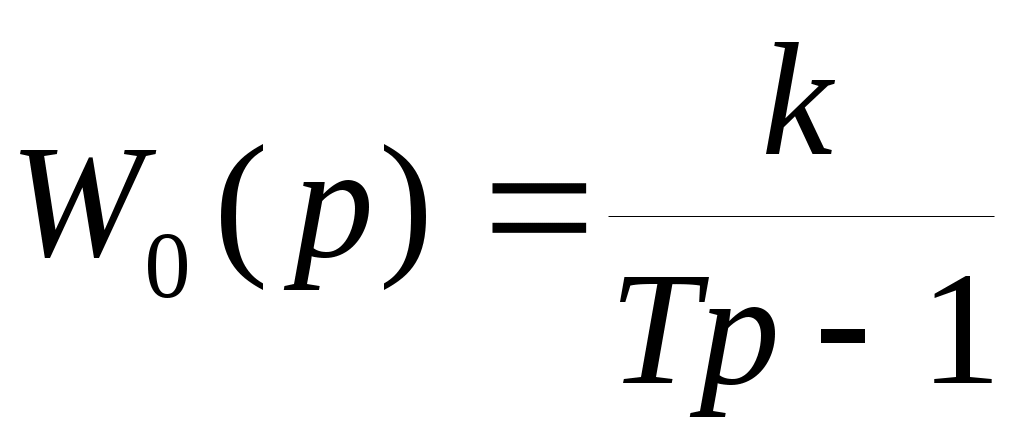
    
26. 
    Задавайте малое начальное отклонение х₁₀ и пронаблюдайте фазовый портрет при отсутствии коррекции по скорости. Каков Ваш вывод о работоспособности системы управления?
    
27. 
    Введите коррекцию по скорости =0,2. Постепенно увеличивая начальное отклонение х₁₀ , сделайте вывод о возможных режимах работы системы управления. Полученные результаты зафиксируйте в виде фазовых портретов и графиков х₁(t) и x₂(t).
    
28. 
    Определите величину начального отклонения, которое при =0,2 система не может устранить. Увеличивая степень коррекции по скорости, добейтесь наблюдения сходящего процесса. Попытайтесь выделить и пронаблюдать на экране индикатора границу между двумя качественно отличными режимами работы системы управления. Какие Вы испытываете затруднения? Объясните их причину.
    
29. 
    Реализуйте релейную характеристику с зоной нечувствительности, задавая d0 и m=1.
    
30. 
    При наличии коррекции по скорости исследуйте динамику системы управления, задавая малые отклонения в соответствии с условиями: х₁₀ <0; х₁₀ >0, при х₁₀ =0.
    
31. 
    При наличии коррекции по скорости и больших начальных отклонениях проварьируйте величину коррекции и зарисуйте фазовые портреты и графики х₁(t) и x₂(t).
    
32. 
    Реализуйте релейную характеристику с гистерезисом и зоной нечувствительности, задавая d0 и 0<m<1.
    
33. 
    Изменяя величину коррекции по скорости, при начальном отклонении х₁₀>d, пронаблюдайте вид фазовых траекторий. Сравните внешний вид фазовых траекторий, полученных при сильной коррекции по скорости, для случая однозначной и неоднозначной характеристик реле с зоной нечувствительности.
    
34. 
    По результатам пп. 24-33 сделайте вывод о динамических свойствах системы управления динамическим объектом с передаточной функцией вида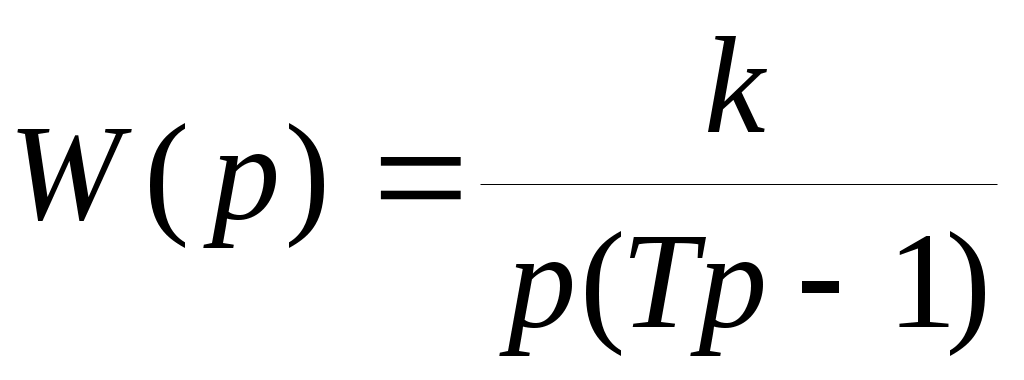 , рассматривая случаи однозначных и неоднозначных релейных характеристик.
    

---

Таблица 9

№	1	2	3	4	5	6	7	8	9
k	1,1	9,4	4,6	5,7	2,2	8,3	3,5	6,8	7,9
T	0,44	0,36	0,85	0,22	0,73	0,58	0,11	0,96	0,69

Контрольные вопросы:

1. 
   Почему метод фазовой плоскости относят к точным методам исследования нелинейных систем ?
   
2. 
   Какие Вам известны типы особых линий ?
   
3. 
   Что такое предельный цикл?
   
4. 
   Какие типы предельных циклов Вам известны ?
   
5. 
   Что называется линией переключения ?
   
6. 
   Как построить линию переключения ?
   
7. 
   Что такое скользящий режим ?
   
8. 
   Как установить возможность возникновения в системе управления скользящего режима ?
   
9. 
   В чем особенность фазового портрета для систем управления с неоднозначными нелинейностями ?
   
10. 
    Как по фазовой траектории определить поведение системы во времени ?
    

ЛАБОРАТОРНАЯ РАБОТА 10

Исследование нелинейных систем методом

гармонического баланса
Цель работы: практическое овладение методом гармонического баланса для анализа устойчивости замкнутых нелинейных систем; определение условий возникновения незатухающих периодических колебаний и нахождение параметров автоколебаний.
Краткие теоретические сведения

В соответствии с критерием устойчивости Найквиста незатухающие колебания в линейной системе возникают в том случае, когда амплитудно-фазовая характеристика разомкнутой системы проходит через точку с координатами [-1, j0]. Данное условие является также условием существования автоколебаний в гармонически линеаризованный нелинейной системе, т.е.

W_н(jw, a) = -1.

Так как линейная и нелинейная части системы соединены последовательно, то частотная характеристика разомкнутой нелинейной системы имеет вид

W_н(jw, a) = W_лч(jw)*W_Э(jw, a).

Тогда в случае статической характеристики нелинейного элемента условие принимает вид

---

W_лч(jw) = - .

Решение уравнения относительно частоты и амплитуды автоколебаний можно получить графически как точку пересечения годографа частотной характеристики линейной части системы W_лч(jw) и годографа обратной характеристики нелинейной части - , взятой с обратным знаком. Если эти годографы не пересекаются, то режим автоколебаний в исследуемой системе не существует.


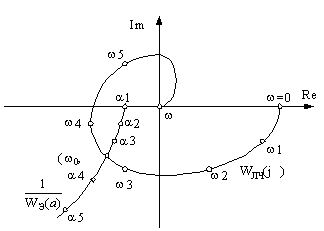Рис.36. Годографы линейной и нелинейной частей системы
Для устойчивости автоколебательного режима с частотой w₀ и амплитудой a₀ требуется, чтобы точка на годографе нелинейной части - , соответствующая увеличенной амплитуде a₀+Δa по сравнению со значением в точке пересечения годографов, не охватывалась годографом частотной характеристики линейной части системы и охватывалась точка, соответствующая уменьшенной амплитуде a₀-Δa.

На рис.36 дан пример расположения годографов для случая, когда в нелинейной системе существуют устойчивые автоколебания, так как a₃ < a₀ < a₄ .
Задание и порядок выполнения лабораторной работы

1. 
   Структурная схема исследуемой системы управления представлена на рис.37. В результате теоретического анализа определите возможность возникновения в этой системе режима автоколебаний для нелинейностей и передаточные функций, приведенных в табл.10, постоянную времени Т, брать из табл.11, согласно своему варианту. Клетки таблиц заполните ответами, указав для однозначных нелинейностей расчетные значения параметров автоколебаний.
   
2. 
   Разработайте методику исследования режима автоколебаний на ЭВМ. Проверьте моделированием теоретические результаты п. 1.
   
3. 
   Разомкните обратную связь и на вход сумматора подайте гармонический сигнал. Изучите форму сигналов на выходе нелинейности, а также на выходе первого, второго и третьего апериодических звеньев, варьируя частоту входного сигнала, для всех нелинейностей указанных в табл.10. Отметьте, как в графиках сигналов проявляется фильтрующее свойство линейной части системы управления.
   
4. 
   Замкните обратную связь. Реализация последнего из апериодических звеньев с использованием сумматора, позволяет получить сигнал, пропорциональный производной от сигнала на выходе линейной части системы управления. Используя эту возможность, пронаблюдайте фазовые траектории исследуемой системы управления, рассматривая линейную часть с передаточной функцией вида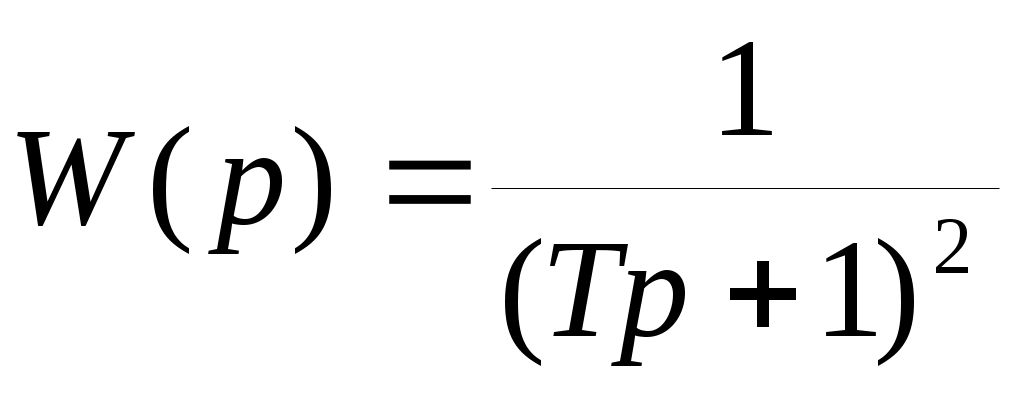 и нелинейности указанные в табл.10.
   
5. 
   Варьируя начальные условия или амплитуду входного сигнала, зафиксируйте фазовые траектории, соответствующие устойчивым и неустойчивым предельным циклам. Изучите процессы установления автоколебаний и зафиксируйте графики.
   

---

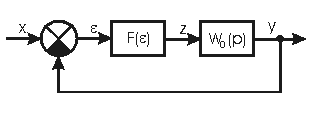
Рис.37
Таблица 10

	F()	W0(p)
1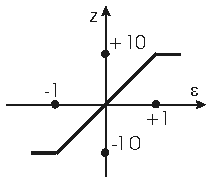
2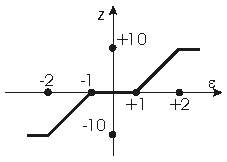
3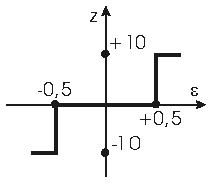
4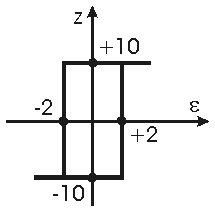

Таблица 11

№	1	2	3	4	5	6	7	8	9	10
Т	0,9	0,15	0,7	0,45	0,3	0,6	0,28	0,5	0,75	0,9

Контрольные вопросы

1. 
   Сформулируйте общую постановку задачи анализа нелинейной системы методом гармонического баланса.
   
2. 
   Какие допущения лежат в основе метода гармонического баланса ?
   
3. 
   Что позволяет определить – метод гармонического баланса в результате анализа нелинейной и системы ?
   
4. 
   Что такое автоколебания ?
   
5. 
   Какой вид имеет уравнение Гольдфарба и что оно описывает ?
   
6. 
   Какие Вам известны способы решения уравнения Гольдфарба?
   
7. 
   Сформулируйте понятие устойчивости система управления в режиме автоколебаний?
   

---